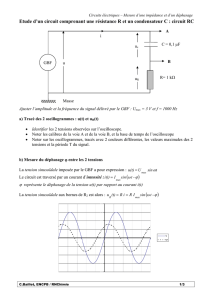
Dipôles passifs en régime sinusoïdal : Cours de physique

1et_ch9 (Complexes_RLC_sinusoïdal).odt - Marie Pierrot – Lycée du Rempart - 20/05/10
Ch.9 : Dipôles passifs en régime sinusoïdal.
1. Nombres complexes associés aux vecteurs de Fresnel.
Le vecteur de Fresnel:
Son module est la valeur efficace de la grandeur u(t) qu'il représente.
est la phase à l'origine de u(t).θ
On peut lui associé un nombre complexe:
U=U∙cosθj∙U∙sinθ
U = U et = Arg (θU)
j est un nombre complexe tel que: j2 = -1 et
1
jj= −
.
Un vecteur tout comme un nombre complexe nous permet de caractériser une grandeur sinusoïdale en nous indiquant
son amplitude et sa phase à l'origine.
Exercice d'application n°1
Dessiner les vecteurs de Fresnel et donner l'écriture complexe des tensions ci – contre :
2. Les dipôles passifs en régime sinusoïdal
2.1. Caractéristiques d'un dipôle passif linéaire
Les dipôles passifs sont la résistance, le condensateur et
l'inductance.
Lorsque on applique une tension sinusoïdale
u=U
2∙sinω∙t
,
de fréquence donnée, à un dipôle passif linéaire, il est traversé par
un courant sinusoïdal
i=I
2∙sinω∙ t−φ
de même fréquence
que la tension et tel que U et I sont proportionnels :
U=Z∙I
Z est appelée impédance du dipôle et s'exprime en Ohm – - Ω
est le déphasage entre la tension et l'intensité en radians – rad- ; = φ φ θU – θI
Un dipôle passif linéaire est caractérisé par son impédance Z et le déphasage qu'il produit entre la tension à sesφ
bornes et l'intensité du courant qui le traverse.
Rmq: on définie également Y = 1/Z, appelée admittance et qui s'exprime en Siemens -S-.
Exercice d'application n°2 : Un dipôle passif soumis à une tension
u=16
2∙ sin9525∙t−
6
est traversé par un
courant d'intensité
i=0,008
2∙ sin9525∙t
12
.
1) Dessiner les vecteurs de Fresnel associés à chacune de ces grandeurs
2) Déterminer les nombres complexes qui leur sont associés
3) Déterminer les éléments caractéristiques du dipôle passif Z et .φ
2.2. Impédance complexe des dipôles élémentaires.
I et U sont les nombres complexes associés aux vecteurs
I
et
U
.
La loi d'Ohm s'écrit avec les complexes :
Z est l'impédance complexe du dipôle élémentaire : Z = [ Z ; ]φ
Exercice d'application n°3 : Reprendre l'exercice précédent et déterminer l'impédance complexe Z du dipôle passif,
sous la forme trigonométrique et sous la forme algébrique. Calculer le rapport U / I . Conclusion ?
Page 1 sur 5
O x
U
U
θU
Dipôle passif
Z ; φ
u=U
2 ∙sinω∙ t
i=I
2∙sinω∙t−φ
U1=5
U2=j∙4
U3=−3
U4=−j∙2
U5=2,9−j∙5
u1=5∙
2 ∙sinω∙t
u2=4 ∙
2∙sinω∙t
2
u3=3 ∙
2∙sinω∙t
u4=5,8∙
2 ∙sinω∙t−
2
u5=5,8∙
2∙sinω∙ t−
3
Réponses :
U = Z.I
⇒Z=U
I=[U ;0]
[I ;−φ]= [Z ;φ]

1et_ch9 (Complexes_RLC_sinusoïdal).odt - Marie Pierrot – Lycée du Rempart - 20/05/10
2.3. Résistance.
Entre les valeurs instantanées du courant et de la tension on a la relation: u = R i
si i=I
2 sintωalors u=RI
2 sin
tω
avec U=RI
Exercice d'application n°4
Déterminer le déphasage entre u et i et le module de l'impédance Z = U / I
En déduire la valeur de la résistance.
Les caractéristiques du résistor linéaire sont: Z = R et ϕ = 0 rad
Impédance complexe:
Les vecteurs de Fresnel
I
et
U
sont colinéaires et on peut écrire U = R.I entre les grandeurs complexes associées.
→L'impédance complexe d'une résistance est réelle :
2.4. Bobine parfaite (inductance).
Entre les valeurs instantanées du courant et de la tension on a la relation:
u=Ldi
dt
Exercice d'application n°5
Déterminer le déphasage entre u et i et le module de l'impédance Z = U / I
En déduire la valeur de l'inductance de la bobine.
Page 2 sur 5
ZR = R
i
u
R
Tension u :
Amplitude 4,23 Volt
Valeur efficace 2,99 Volt
Phase à l'origine 0 degrés
Fréquence 100 Hertz
intensité i
Amplitude 9mA
Valeur efficace 6,36mA
Phase à l'origine 0 degrés
Fréquence 100 Hertz
On en déduit :
x y
Vecteur 1 2,99 0
Vecteur 2 6,36 0
Caractéristique de l'impédance
Déphasage 0 degrès
Module 470 ohms
2
0 1 2 3 4 5 6 7 8 9 10
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
u(t) (V)
i(t) (mA)
temps en millisecondes
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
i
u
L
Tension u :
Amplitude 5 Volt
Valeur efficace 3,54 Volt
Phase à l'origine 90 degrés
Fréquence 100 Hertz
intensité i
Amplitude 8 mA
Valeur efficace 5,66 mA
Phase à l'origine 0 degrés
Fréquence 100 Hertz
On en déduit :
x y
Vecteur 1 0 3,54
Vecteur 2 5,66 0
Caractéristique de l'impédance
Déphasage 90 degrès
Module 625 ohms
2
0 1 2 3 4 5 6 7 8 9 10
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
u(t) (V)
i(t) (mA)
temps en millisecondes
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
si i=I
2sin
tωθI
alors u=Ld
dt
[
I
2sin
tωθI
]
=LI
2⨯ωcos
tωθI
u=L Iω
2sin
tωθIπ
2
et comme u=U
2sin
tωθU
Ona:U=L Iωet φ=θU−θI= π
2rad

1et_ch9 (Complexes_RLC_sinusoïdal).odt - Marie Pierrot – Lycée du Rempart - 20/05/10
Les caractéristiques de la bobine parfaite sont: Z = Lω et ϕ = +π/2 rad
Impédance complexe:
Loi d'Ohm en complexe: UL = ZL.I
Relation entre les modules : UL = LωI
On peut écrire : UL = [ L I ; ω
2
] = jLωI car
UL
est sur l'axe des imaginaires purs.
→L'impédance complexe d'une bobine parfaite est : ZL = [ L ; ω
2
] = jLω
2.5. Condensateur parfait (capacité).
Entre les valeurs instantanées du courant et de la tension on a la relation:
i=Cdu
dt
Exercice d'application n°6
Déterminer le déphasage entre u et i et le module de l'impédance Z = U / I
En déduire la valeur de la capacité du condensateur.
Les caractéristiques du condensateur parfait sont: Z = 1/Cω et ϕ = -π/2 rad
Impédance complexe:
Loi d'Ohm : UC = ZC.I
Relation entre les modules : UC = (1/Cω)×I
On peut écrire : UC = [
1
Cω
∙I ;
−
2
] = -j ×(1/Cω) × I
→L'impédance complexe d'un condensateur parfaite est : ZC = [
1
Cω
;
−
2
] = 1/jCω
2.6. Généralisation
L'impédance complexe Z introduit le déphasage entre U et I et contient la proportionnalité entre les valeurs efficaces :
et
Page 3 sur 5
i
u
C
Tension u :
Amplitude 7 Volt
Valeur efficace 4,95 Volt
Phase à l'origine -90 degrés
Fréquence 100 Hertz
intensité i
Amplitude 5 mA
Valeur efficace 3,54 mA
Phase à l'origine 0 degrés
Fréquence 100 Hertz
On en déduit :
x y
Vecteur 1 0 -4,95
Vecteur 2 3,54 0
Caractéristique de l'impédance
Déphasage -90 degrès
Module 1400 ohms
2
0 1 2 3 4 5 6 7 8 9 10
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
u(t) (V)
i(t) (mA)
temps en millisecondes
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
si u=U
2 sin
tω
alors i=Cd
dt
[
U
2sin
tω
]
=CU
2⨯ωcos
tω
u=C Uω
2 sin
tωπ
2
et comme i=I
2sin
tω−φ
On a alors: I=C Uωou U=I
Cωet φ=θU−θI= −π
2rad
U=Z⨯I⇒
{
U=Z⨯I
φ=θU−θI=Arg Z
Z=[ Z ;φ]

1et_ch9 (Complexes_RLC_sinusoïdal).odt - Marie Pierrot – Lycée du Rempart - 20/05/10
Exercice d'application n°7
1) Déterminer le déphasage entre u et i et le module de l'impédance Z = U / I
2) En déduire l'impédance complexe Z sous la forme trigonométrique puis sous la forme algébrique.
3) Ce dipôle possède une résistance. Est-il selon vous plutôt inductif ou plutôt capacitif ?
4)
i=3,54∙10−3∙
2∙sinω∙t
4
. Exprimer l'intensité complexe I sous la forme trigonométrique.
5) En déduire la tension complexe U en utilisant la loi d'Ohm complexe.
6) Votre résultat correspond-il aux données concernant u ?
3. Tableau récapitulatif
Dipôle RESISTOR PARFAIT REACTOR PARFAIT CONDENSATEUR PARFAIT
Représentation
Lois d'Ohm:
U = Z I
U=R I
U=jLωI
U=1
jCωI
Impédance Z (Ohm - -)Ω
ZR=[ R; 0]=R
ZL=[Lω;π
2]= jLω
ZC=[ 1
Cω;−π
2]= 1
jCω
Admittance Y (Siemens -S-)
Y=1
Z
YR=[ 1
R;0]= 1
R
YL=[ 1
Lω;−π
2]= 1
jLω
YC=[Cω;π
2]= jCω
Représentation des vecteurs
de Fresnel associés à u et i
Comportement aux
basses fréquences
Comportement aux
hautes fréquences
Page 4 sur 5
Tension u :
Amplitude 6 Volt
Valeur efficace 4,24 Volt
Phase à l'origine -20 degrés
Fréquence 100 Hertz
intensité i
Amplitude 5mA
Valeur efficace 3,54mA
Phase à l'origine 45 degrés
Fréquence 100 Hertz
On en déduit :
x y
Vecteur 1 3,99 -1,45
Vecteur 2 2,5 2,5
Caractéristique de l'impédance
Déphasage -65 degrès
Module 1200 ohms
2
0 1 2 3 4 5 6 7 8 9 10
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
u(t) (V)
i(t) (mA)
temps en millisecondes
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
O
U
IOU
I
ϕ
O
U
Iϕ
i
u
R
i
u
Li
u
C
R
R

1et_ch9 (Complexes_RLC_sinusoïdal).odt - Marie Pierrot – Lycée du Rempart - 20/05/10
4. Association RLC série.
Problème: Connaissant R, L et C, trouvons l'impédance Z de l'ensemble.
On peut appliquer la loi d'additivité des tensions avec les notations complexes:
U=URULUC
U=R IjLωI1
jCωI
U=RjLω1
jCωI
Z=RjLω1
jCω
Z=RjLω−1
jCω
et
Z=RjLω−1
Cω
⇨
∣
Z
∣
=Z=
R2Lω−1
Cω
2
φ=ArgZ⇒ φ=Arctg[
Lω−1
Cω
R]
Exercice d'application n°12
Trois dipôles R = 820 ; L = 0,3 H et C = 0,47 µF sont associés en série. Ωf = 800 Hz.
1) Déterminer Z
2)
i=0,007
2∙ sinω∙ t−
6
.Déterminer u.
5. Association RLC parallèle.
Problème: Connaissant R, L et C, trouvons l'impédance Z de l'ensemble.
On peut appliquer la loi des nœuds avec les notations complexes:
I=IRILIC
I=U
RU
jLωjCωU
I=1
R1
jLωjCωU
I=1
R−j1
LωjCωU
I=[1
RjCω−1
Lω]U
U=1
[1
RjCω−1
Lω]
I
enfin
Z=1
[1
RjCω−1
Lω]
⇨
Z=1
1
R
2
Cω−1
Lω
2
φ=Arctg[R1
Lω−Cω]
Exercice d'application n°13
Trois dipôles R = 820 ; L = 0,3 H et C = 0,47 µF sont associés en parallèle. Ωf = 800 Hz.
1) Déterminer Y puis en déduire Z
2)
i=0,007
2∙ sinω∙t−
6
.Déterminer u.
6. Conclusion
Quand les dipôles sont en série leurs impédances complexes s’ajoutent pour donner
l’impédance complexe de l’association.
ZR = R ; ZL = jLω ; ZC = 1/ jCω et
Z=RjLω−1
Cω
Quand les dipôles sont en parallèle leurs admittances complexes s’ajoutent pour donner
l’admittance complexe de l’association.
YR = 1/R ; YL = 1/jLω ; YC = jCω et
Y=1
RjCω−1
Lω
Page 5 sur 5
i
uR
R
uL
L
uC
C
u
RLC
R
L
C
i
iR
R
iL
L
iCC
u
1
/
5
100%