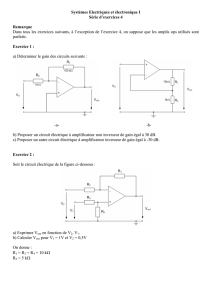
ElectroCinetique II

de
Bourges
L'école de la
maîtrise des risques
INSTITUT NATIONAL
DES SCIENCES
APPLIQUÉES
CENTRE VAL DE LOIRE
INSA
Campus
1ER CYCLE INGÉNIEUR DE L’ENSI DE BOURGES
UE SCIENCE APPLIQUÉES
SUPPORT DE COURS
D’ÉLECTROCINÉTIQUE II
David FOLIO <[email protected]>
http://perso.ensi-bourges.fr/dfolio/Teaching.php
L’objet de se support de cours n’est pas de fournir le cours complet d’électrocinétique. Il s’agit plutôt
d’un guide pour vous aider à suivre et comprendre le cours. Il vous appartient de le compléter et de
l’enrichir des différents éléments abordé en cours et en TD.
Année Universitaire : 2013–2014

ii
Cycle 1, INSA-CVL, ÉlectroCinétique II

Table des matières
IV Régime sinusoïdal 1
IV.1Lessignauxélectriques.................................... 1
IV.2 Représentation d’une grandeur sinusoïdale . . . . . . . . . . . . . . . . . . . . . . . . . 3
IV.3 Circuits en régime sinusoïdal forcé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
IV.4 Puissances en régime alternatif . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
V Réponses fréquentielles 17
V.1 Introduction.......................................... 17
V.2 Réponse en fréquence des circuits linéaires . . . . . . . . . . . . . . . . . . . . . . . . . 19
V.3 Filtrageanalogique...................................... 25
VI Amplificateurs 31
VI.1L’Amplification........................................ 31
VI.2 L’Amplificateur Opérationnel (AOP) . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
A Références Bibliographiques 41
iii

TABLE DES MATIÈRES iv
Cycle 1, INSA-CVL, ÉlectroCinétique II

Chapitre IV
LE RÉGIME VARIABLE SINUSOÏDAL
L’objectif est d’étudier le comportement des circuits linéaires lorsqu’ils sont soumis à un signal
électrique variable. Plus particulièrement, on s’intéressera aux signaux alternatifs sinusoïdaux.
IV.1 Les signaux électriques
Un signal électrique peut être caractérisé par sa forme : continue ou variable, périodique ou
non, unidirectionnel ou alternatifs, etc. On distingue également :
les signaux analogiques : variation continue dans le temps des signaux électriques
,→Information : valeurs instantanées des grandeurs électriques
les signaux numériques : variation binaire des signaux électriques
,→Codage de l’information
IV.1.1 Le régime variable
Contrairement au régime continu où les grandeurs électriques sont constantes par rapports
aux temps, les grandeurs du régime variable évoluent en fonction du temps.
τT
Sinus Carré Triangle
Dents de scieSinc Train d'impulsion
exp(-t/τ)
Fig. IV.1 – Quelques exemples de signaux variables
IV.1.2 Les signaux périodiques
Parmi la multitude de signaux variables, on s’in-
téresse principalement aux signaux électriques
périodiques.
Définition 1 (Signaux périodiques).Un si-
gnal temporel est périodique de période Tssi :
x(t+kT ) = x(t),∀t∈R+,∀k∈N(IV.1)
t
1