Un nouveau modGle de la zone de contact outil copeau

C. R. Acad. Sci. Paris, t. 328, Skrie II b, p. l-4, 2000
MCcanique des milieux continus/Continuum mechanics
Un nouveau modGle de la zone
de contact outil copeau
Olivier CAHUC, Didier TOULOUSE, Yves COUl?TARD, Alain Gl&ARD
Laboratoire de mkcanique physique (CNRS UMR 5469), U mversith Bordeaux-l (Sciences et technologies),
351, cows de la Lib&ation, 33405 Talence cedex, France
(Note prt5sentCe le 16 mars 1999, accept6 aprb rkvision le 26 juillet 1999)
R&sum&
Pour l’ktude de la mise en forme par enlbvement de matibre now d6veloppons une
modClisation de la zone de contact outil copeau fondle sur la notion de couples de
contraintes. Nous prksentons les principales hypothkses et les rbultats issus d’un
modkle 3D de coupe analytique associk. 0 2000 Acadkmie des scienceskditions
scientifiques et mkdicales Elsevier SAS
couple de contraintes / thermoviscoplasticit6 / usinage
An modelling for contact between tool and ship
Abstract.
In the study of the cutting, we develop a model for the contact between ship and
tool based on the notion of stress couple. We present the main hypotheses for the
associated 30 analytic model and the results arising premil. 0 2000 Acade’mie des
scienceskditions scientijques et mkdicales Elsevier SAS
torque stress / thermoviscoplustici@ /cutting metal
1. Introduction
L’enlbvement de mat&e soumet une pike B de grandes dkformations (et 5 de grandes vitesses de
dkformation) [l]. Les modklisations analytiques de ces phknomknes sont peu nombreuses et g&kale-
ment 2D [2]. Les simulations numkiques assocides [l-4] s’appuient t&s souvent sur les lois de contact
de Coulomb. L’expkrience montre que les effets visqueux sont d’autant plus importants que les vitesses
de sollicitation sont ClevCes. Des zones dites << collantes >> apparaissent entre copeau-outil et conduisent
g pressentir la prksence de densite de couples de contraintes. Cette densit contribue au moment
rksultant des actions exerckes et mesurkes g la pointe de l’outil [5]. Sur ces bases, nous proposons un
modkle analytique 3D.
2. ModClisation
Nous limitons l’ttude aux matkriaux homogtines, isotropes, plastiquement incompressibles B seuil de
Von Mises, en rkgime stationnaire. Les deformations (et vitesses de) sont calcul&es selon la dkmarche
[6] modifike par le choix d’une repartition originale des contraintes le long des zones de cisaillement,
Note prksentie par Mlchel COMBARNOUS.
1287-4620/00/032801 0 2000 Acadhie des scienceshditions scientifiques et mkdicales Elsevier SAS.
Tous droits r&en&
1

0. Cahuc et al.
et aux interfaces entre outil-copeau autorisant ainsi la prise en compte de don&es expCrimentales IS].
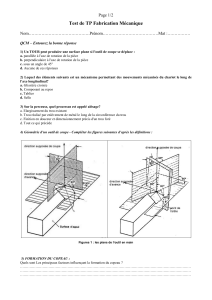
Les lignes d’koulement dans le copeau sont assimilCes ti des hyperboles (&we I). Le cisaillement
primaire co’incide avec une zone OA d’epaisseur hl inclinke d’un angle Q, par rapport B la direction de
la vitesse de coupe Vc 171. L’Cpaisseur du copeau est 4! Cf;swe I). La particule qui traverse la zone OA,
subit une (vitesse de) d~fo~ation ( joA ) yoA.
Outii
Pi&e 0
Figure 1. Lignes d’tcoulement.
Figure 1. Lines ofJow.
La zone de cisaillement secondaire (type << couche limite 3)) i l’interface entre l’outil et le reste du
copeau est assimil&e B un milieu micropolaire d’kpaisseur 6 x e @gure I) ntgligeable lors du calcul de
la puissance dissipke selon la dCmarche [7]. La longueur Y de contact outil-copeau coincide avec la
longueur du cisaillement secondaire UB oi3 le profil des vitesses est dond $gure 2. La diformation
gCnCralide Eoe est suppode saturke.
Figure 2. Repartition des contraintes sur OA, OB et OK.
Figure 2. Distribution of sfress on OA, OB and OK.
Compte tenu de la loi de comportement de type Norton Hoff retenue pour la zone de cisaillement
primaire, la temptrature moyenne 8, le long de OA est obtenue par ksolution de 1’Cquation de
l’energie et fait intervenir l’indice d’krouissage FZ, l’indice de viscositk m, la masse volumique p, la
chaleur spkifique c, la tempkrature ambiante Q0 et des coefficients A et B de la loi de comportement.
La r&partition des contraintes de cisaillement et des pressions hydros~tiques yigure 2) s’obtient
ctassiquement. La pression sur OA est don& par la densite p( x ) [ES]. Le cisaillement est ddduit
constant dans cette zone. Suivant OB la pression vaut PO sur OC et dCcroit depuis C pour s’annuler en
PO (Y-y’)
B telle que p( y’) = l-k y ‘dy’ E [ kY, Y], 0 < k < 1. Le r&e1 k est CvaluC pour que 1’Cnergie
2

Un nouveau modtile de la zone de contact outil copeau
consommee par le moment des actions en 0 soit minimale. Dans la zone OB, le cisaillement vaut ooB
sur OC et decroit depuis C pour s’annuler en B. Du fait du contact collant outil-copeau, dans la
<c couche lirnite )> le ma&au devient de nature differente et done a un comportement different. Ceci
conduit a modeliser cette << couche limite >> par un milieu micropolaire [9] pouvant developper des
couples de contraintes en conformite avec les observations effectuees. 11 en resulte un tenseur des
contraintes non symetrique [lo]. Nous retenons pour loi de comportement de ce milieu rnicropolaire un
seuil constant Cgal a m pour le tenseur des couples de contraintes. Nous admettons alors simplement
que les couples de contraintes Cvoluent en fonction de la deformation de rotation Oint selon les donntes
figure 4.
Ce choix de comportement permet de satisfaire pleinement, d’une part la continuite des contraintes
internes entre cette << couche lirnite B et le reste du copeau et, d’autre part, la condition a la limite des
moments mesures a la pointe de l’outil [5]. Pour decrire les evolutions des actions mecaniques exercees
par le copeau sur l’outil, nous utilisons le rep&e (P ; x, y, z) defini jgure 3.
Figure 3. DCfinition des composantes.
Figure 3. Dejnition of components.
Figure 4. fivolution de la densitk de couple de contra&e en
fonction de la deformation de rotation moyenne.
Figure 4. Evolution of torque’s stress density with the average
rotation deformation.
3. RCsultats
La loi de comportement [6] utiliste pour d&ire le comportement thermoviscoplastique Ccrouissable
du mat&au pendant la coupe est : 8 = 2; $( A - Be) a laquelle il convient d’adjoindre, pour la
<< couche limite Y la loi a seuil constant pour le tenseur des couples de contraintes. La valeur de la
constante k est alors calculee en minimisant le couple applique sur la face de coupe. Puis sont Cvalues,
la longueur de contact Y, la valeur seuil m du couple de contrainte appliquee sur OC et l’bpaisseur du
cisaillement primaire hi.
3

0. Cahuc et al.
L’usinage d’une piece d’acier 42CD4 a Cte effectue et simule. Les six composantes du torseur
representatif des actions de coupe a la pointe de l’outil, simultes ou mesurees, sont repertoriees dans
les deux premieres lignes du tableau suivant. La troisieme ligne montre les resultats obtenus a l’aide du
modble de Merchant.
Fx 0’) FY (N) Fz (NJ Mx (Nm) MY OW Mz (Nm) P calcul~e
W)
Simul6e 3D 992 436 369 - 11,6 9,47 - 4,85 2 615
Mesurte 3D 1006 485 391 - 11,96 6,72 - lo,84 2 460
Simulation 2D (Merchant) 985 438 *** *** *** *** 1 972
Mesuree 2D 1006 485 **** *** *** *** 2 012
Cet exemple de confrontation simulation-experience est globalement satisfaisant dans la mesure ou
le torseur d’action est simule avec une erreur inferieure a 10 % (equivalent a la precision des mesures)
pour la resultante g&kale et de l’ordre de 30 % en moyenne pour les composantes du couple (sauf
pour Mz oti l’ecart releve est imputable, surtout, a de possibles erreurs de mise en position angulaire).
La puissance Clectrique mesuree au moteur est PE = 3 050 W. Le rendement mecanique du tour est de
q = 0,815 pour cette puissance. La puissance Clectrique consommee par la coupe est done
PEc = 2 592 W (a comparer a la puissance mecanique calculee P caZcuZe’e avec les differents
modeles). Ces resultats permettent done de valider clairement ce modele 3D.
4. Conclusion
Cette etude montre bien la necessite de prendre en consideration dans la modelisation la notion de
couples de contraintes que toute liaison complete peut transmettre des qu’il y a des deformations de
rotation.
RCf&ences bibliographiques
[l] Oxley P.L.B., Stevenson M.G., Measuring stress/strain properties at very high strain rates using a machining test, J. Inst. of
Met. 95 (1967) 308-313.
[2] Moutki A., MolinariA., Dudzinski D., Modelling orthogonal cutting with temperature dependent friction law, J. Mech.
Phys. Sol. 46 (1998) 2103-2138.
[3] Marusich T.D., Ortiz M., Modelling and simulation of high-speed machining, Int. J. Num. Meth. in Eng. 38 (1995)
3675-3694.
[4] Boothroyd G., Temperatures in orthogonal metal cutting, Proc Inst. Mech. Engng. 117 (1963) 789-802.
[5] Toulouse D., Cotretard Y., Cahuc O., Gerard A., An experimental Method for the cutting Process in three dimensions,
DYMAT, Toledo, Spain, 22-26 Sept., 1997, pp. 21-26.
[6] Gilormini P., Contribution B la modelisation de la formation du copeau en usinage des mttaux, These Universite Paris VI
(1982).
[7] Oxley P.L.B., Hasting W.F., Minimum work as possible criterion for determining the frictionnal conditions at the tool
interface in machining, Phil. Trans. Roy. Sot. Lond. 282 (1976) 565-584.
[8] Toulouse D., Contibution a la modtlisation et a la metrologie de la coupe darts le cas d’un usinage tridimensionnel, These
Universite Bordeaux I, 1998.
[9] Cosserat E., Cosserat F., Sur la thtorie de l’tlasticite, Ann. Fat. Sci. Toulouse (1896).
[lo] Salencon J., Mtcanique des milieux continus, Tome 1, Ellipse, 1988.
4