Exercices sur le chapitre I (thème 1)

Page 1 sur 3
Exercices sur le chapitre I (thème 1) : Une première présentation de l’Univers
D’après Physique Chimie 2de(nouveau programme), Collection Dulaurans Durupty, Hachette Education
Exercice 1
1. Classer, par ordre croissant de taille, les objets suivants : atome ; galaxie ; Homme ; Lune ;
noyau d’atome ; Soleil ; système solaire ; Terre ; Univers.
2. Que trouve-t-on entre le noyau d’un atome et ses électrons ?
3. Que trouve-t-on essentiellement entre les étoiles d’une galaxie ?
Exercice 2
Lors des missions lunaires, des miroirs ont été placés sur la Lune. Depuis l’observatoire de Calern, près
de Nice, un puissant faisceau laser est dirigé vers la Lune. Ce faisceau se réfléchit sur les miroirs et
revient à l’observatoire.
Une mesure de la durée de l’aller-retour du faisceau entre la Terre et la Lune a donné t=2,56442 s.
Donnée : c = 2,99792458 x 108 m.s-1.
1. Faire un schéma montrant le trajet de la lumière lors de cette mesure.
2. Rappeler la relation entre la distance d parcourue, la durée du parcours t et la valeur de la
vitesse c.
3. Déterminer la longueur d du trajet parcouru par la lumière lors de cette mesure.
4. En remarquant que la lumière effectue un aller-retour entre la Terre et la Lune, déterminer la
distance D, séparant la Terre et la Lune lors de la mesure.
Exercice 3
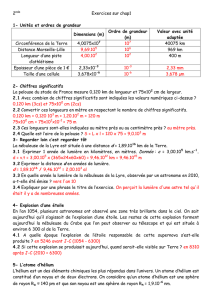
Reproduire et compléter le tableau suivant :
Dimensions
Dimensions (en m)
et en notation
scientifique
Ordre de grandeur
(en m)
Valeur avec une
unité adaptée
Circonférence de la
Terre
40,075 millions
de mètres
Distance Bogotá-
Santa Marta
904 km
Longueur d’une
piste d’athlétisme
400 m
Epaisseur d’une
piece de 1 €
………. cm
2,33 x 10-3
Taille d’une cellule
3678 nm
Données :
- L’ordre de grandeur d’une valeur numérique est la puissance de 10 la plus proche.
- Voir autres données en annexe

Page 2 sur 3
Exercice 4
La nébuleuse de la Lyre est située à une distance d=1,89 x 1016 km de la Terre.
1. Exprimer la distance d en année de lumière.
2. En quelle année la lumière de la nébuleuse de la Lyre, observée par un astronome en 2010, a-t-
elle été émise ?
3. Expliquer alors par une phrase l’expression « regarder loin, c’est remonter dans le passé ».
Exercices supplémentaires
Exercice 5
En 1849, Hyppolyte Fizeau (1819-1896) réalisa à Paris la première mesure de la vitesse de la lumière
dans l’air. A l’aide d’un dispositif de son invention, il mesura la durée du trajet aller-retour de la lumière
entre Montmartre et le Mont Valérien à Suresnes, distants de 8633 m. Il trouva 5,51 x 10-5 s.
1. Quelle est la distance parcourue par la lumière lors de l’aller-retour entre Montmartre et le
Mont Valérien ?
2. Quelle est la valeur de la vitesse de la lumière obtenue par Fizeau ?
Exercice 6
1. En utilisant la notation scientifique, exprimer en mètre les longueurs suivantes :
a. longueur d’un globule rouge : 12m ;
b. longueur d’une molécule d’ADN : 2 nm ;
c. diamètre d’une goutte d’eau : 0,20 mm ;
d. diamètre d’un virus : 90 nm ;
e. rayon de l’atome d’hydrogène : 53 pm.
2. Indiquer l’ordre de grandeur en mètre de chacune de ces longueurs.
Exercice 7
En l’an 1054 plusieurs astronomes ont observé une zone très brillante dans le ciel. On sait aujourd’hui
qu’il s’agissait de l’explosion d’une étoile. Les restes de cette explosion forment aujourd’hui la
nébuleuse du crabe que l’on peut observer au télescope et qui est située à environ 6300 a.l de la Terre.
1. A quelle époque l’explosion de l’étoile responsable de cette supernova s’est-elle produite ?
2. Si cette explosion se produisait aujourd’hui, quand serait-elle visible sur Terre ?
Annexe

Page 3 sur 3
MULTIPLES ET SOUS MULTIPLES DES UNITES
Préfixe
Abréviation
Facteur multiplicatif
MULTIPLES
un milliard
giga
G
109 = 1 000 000 000
un million
mega
M
106 = 1 000 000
mille
kilo
k
103 = 1 000
cent
hecto
h
102 = 100
dix
deca
da
101 = 10
100 = 1
SOUS-MULTIPLES
un dixième
deci
d
10-1 = 0,1
un centième
centi
c
10-2 = 0,01
un millième
milli
m
10-3 = 0,001
un
millionième
micro
10-6 = 0,000001
un
milliardième
nano
n
10-9 = 0,000000001
un
trillardième
pico
p
10-12 = 0,000000000001
NOTATION SCIENTIFIQUE
On dit qu’un nombre est écrit en notation scientifique lorsqu’il est écrit sous la forme :
a x 10b où 1 ≤ a <10 et b est un entier relatif