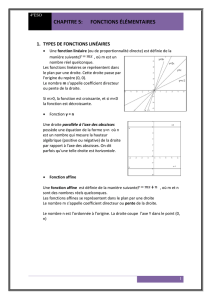
L. Gerin_550.pdf

FF
e
54
2 3
1
6 7
9 1 0 1 1 1 2 1 3 1 4 1 58

H(n)n1
0 10 3
H(10) = 3
n1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
H(n) 0 1 1
k≥0`(k)k
(l(k))k≥0l(k)
k
k≥0k
2kH(2k) = k
H(1092)
a b H(ab) = H(a)+H(b)
n7→ 2n
10
n L(n)
n10 2061983 7
L(2061983) = 7 −1=6 L(8) = 1 −1=0 L(233) = 3 −1=2
L(n)
10L(n)≤n < 10L(n)+1.
102≤233 <103
k≥0L(10k)
a b L(ab) = L(a) +
L(b)
a b L(ab) = L(a) +
L(b)L(90 ×9) = L(810) = 2 6=
L(90) + L(9) = 1 + 0 a b
L(a) + L(b)≤L(ab)≤L(a) + L(b)+1.
BY:
$
\
C

f
x y
f(xy) = f(x) + f(y).
f0f
f
]0,+∞[
f(1)
n≥0f(xn)f(x)x > 0
f(√x)f(x)x > 0
a q ≥1a1/q =q
√a
xq=a.
f(x1/q)f(x)x > 0
p, q a
ap/q = (a1/q)p= (ap)1/q.
f(xp/q)f(x)x > 0
f(1/x)f(x)x > 0
f(xr)f(x)x > 0
r
1/x
BY:
$
\
C

9325594 ×
88235
ln(9325594 ×88235) = ln(9325594) + ln(88235).
e
xln(x)
88235 11.3878
···
9325594 16.0483
ln(9325594 ×88235) = 11.3878 + 16.0483 = 27.4361.
27.4361
xln(x)
822843786590 27.4361
9325594 ×88235 = 822843786590
BY:
$
\
C

a2ib2ji j
H(ab) = H(2i2j)H(a) + H(b) = H(2i) + H(2j)
10k1
a b 10i10ji, j
L(10i10j)L(10i) + L(10j)
10L(a)≤a < 10L(a)+1 10L(b)≤b < 10L(b)+1
f(0)
BY:
$
\
C