Chapitre 2

Lycée Jules Verne 2016-2017
Seconde
Chapitre 2 - Résolution
d’équations et d’inéquations
A. Heliard
I. Equations du premier degré
Ce sont des équations de degré 1, c’est à dire avec une puissance de xégale à 1.
On met les xd’un coté de l’égalité et le reste de l’autre coté.
Principe de la méthode.
Exemples
3x+ 3 =2x−4
x+ 3 = −4−2x
x=−7−3
S={−7}
4x+ 2 = −x−3
5x+ 2 = −3+x
5x=−5−2
x=−1÷5
S={−1}
II. Equations du second degré
1. Equations du type X2=a
•Si a < 0, alors l’équation n’a pas de solutions, on écrit S=∅.
•SI a>0, alors l’équation a deux solutions : X=√aet X=−√a, on écrit S={−√a;√a}.
Principe de la méthode.
Exemples
x2= 9
⇔x= 3 ou x=−3
S={−3; 3}
(2x+ 1)2= 4
⇔2x+ 1 = 2 ou 2x+ 1 = −2
⇔x=1
2ou x=−3 2
S={−3
2;1 2}
2. Equations produit nul
Un produit est nul si et seulement si l’un des facteurs est nul.
Autrement dit , A×B= 0 ⇔A= 0 ou B= 0.
Proposition (Règle du produit nul).
Pour une équation du second degré autre que du type X2=a, on commence par mettre tous les termes du côté
gauche du signe =, de sorte d’avoir "= 0", puis on factorise et on applique la règle du produit nul.
Principe de la méthode.
Exemples
1

Lycée Jules Verne 2016-2017
Seconde
Chapitre 2 - Résolution
d’équations et d’inéquations
A. Heliard
(x+ 1)(3x−3) = 0
⇔x+ 1 = 0 ou 3x−3 = 0
⇔x=−1ou x= 1
S={−1; 1}
(2x+ 4)2= (x−3)2
⇔(2x+ 4)2−(x−3)2= 0
⇔(x+ 7)(3x+ 1) = 0
⇔x+ 7 = 0 ou 3x+ 1 = 0
⇔x=−7ou x=−1
3
S={−7; −1
3}
III. Equations quotient
On met tout au même dénominateur de sorte d’avoir une fraction égale à 0 et on résout "numérateur = 0" avec
"dénominateur 6= 0".
Principe de la méthode.
Exemple
x+ 1
3x−3= 0
⇔x+ 1 = 0 et 3x−36= 0
⇔x=−1et x6= 1
Or quand x=−1, on a x6= 1 donc : S={−1}
IV. Inéquations du premier degré
Les étapes sont les mêmes que pour les équations du premier degré, mais attention il y a des règles à respecter :
•ajouter ou soustraire une nombre de chaque côté de l’inégalité ne change rien au sens de l’inégalité.
•multiplier ou diviser par un nombre strictement positif ne change pas le sens de l’inégalité
•multiplier ou diviser par un nombre strictement négatif change le sens de l’inégalité
Principe de la méthode.
Exemples
3x+ 3 <2x−4
x+ 3 <−4−2x
x < −7−3
S=] − ∞;−7[
−x−364x+ 2
−5x−362−4x
−5x65+3
x>−1÷ − 5
S= [−1; +∞[
V. Résolution graphique d’inéquations
1. Inéquations du type f(x)< k
Lorsque l’on a un graphique, on peut l’utiliser pour résoudre certaines inéquations, attention cependant il ne s’agit que d’une
résolution approchée.
2

Lycée Jules Verne 2016-2017
Seconde
Chapitre 2 - Résolution
d’équations et d’inéquations
A. Heliard
Résoudre une inéquation du type f(x)< k, c’est trouver les nombres réels xdont l’image par fest inférieure
strictement à k.
(cette définition est applicable aux signes >, 6,>)
Définition(s).
1. On trace la droite d’équation y=k
2. On sélectionne la (ou les) partie(s) de la courbe qui se trouvent en dessous de cette droite et on en lit les
abscisses
3. On donne le résultat sous forme d’intervalle (ou sous forme de réunion d’intervalles)
Principe de la méthode (Pour résoudre graphiquement f(x)< k).
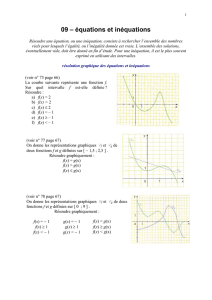
Solutions de :
1. f(x)>3
2. f(x)6−1
3. f(x)>1
Exemple.
2. Inéquations du type f(x)< g(x)
On considère deux fonctions définies sur un même intervalle I.
Résoudre f(x)< g(x)c’est trouver tous les nombres réels x(de l’intervalle I) dont l’image par fest inférieure
strictement à celle par g.
(cette définition est applicable aux signes >, 6,>)
Définition(s).
Il s’agit de déterminer les abscisses des points dont l’image par fest inférieure strictement à celle par g, pour cela
on repère les abscisses des points de Cfsitués en dessous des points de Cg.
Principe de la méthode (Pour résoudre f(x)< g(x)).
3

Lycée Jules Verne 2016-2017
Seconde
Chapitre 2 - Résolution
d’équations et d’inéquations
A. Heliard
1
2
3
4
5
−1
123−1−2−3
Cf
Cg
A
B
Solutions de f(x)>g(x)?
Exemple.
☞ex 74, 75, 76, 78 p 45-46
4