intégration

Intégration sur un segment
Quelques calculs d’aires :
Aire
Aire
Aire
Aire
1
du
du
du
du
rectangle
parallélogramme
triangle
disque de rayon r
l×L
b×h
B×h
2
πr2
Primitives
1.1
Définition - Propriétés
Définition
On dit que la fonction F est une primitive de la fonction f sur l’intervalle I
si F est dérivable sur I et si ∀x ∈ I , F ′ (x) = f (x).
Exemple
3
F : x 7→ x3 + 3 est une primitive sur R de f : x 7→ x2 .
Exemple fondamental :
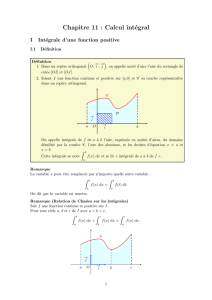
Soit f une fonction continue sur un intervalle [a, b] et Cf sa courbe dans un repère orthonormé.
Pour simplifier, on se placera dans le cas où f est croissante et positive sur [a, b].
On note A la fonction qui à tout réel x ∈ [a, b] associe l’aire de la surface délimitée par Cf et l’axe des
abscisses, entre les abscisses a et x (On admet qu’elle est bien définie sur [a, b]).
C
f
f(x+h)
f(x)
Montrons que A est dérivable en tout x ∈ [a, b]
et que A′ (x) = f (x)
càd que A est une primitive de f sur [a, b].
A(x)
a
x
x+h
b
Posons h > 0 : A(x + h) − A(x) est l’aire comprise entre les abscisses x et x + h.
Par croissance de f , cette aire est comprise entre le petit rectangle de hauteur f (x) et le grand rectangle
de hauteur f (x + h). D’où f (x) × h ≤ A(x + h) − A(x) ≤ f (x + h) × h.
A(x + h) − A(x)
On en déduit que f (x) ≤
≤ f (x + h). Par continuité de f , f (x + h) −→ f (x) et donc,
h→0
h
d’après le théorème d’encadrement, le taux d’accroissement de A admet une limite à droite en x
donc A est dérivable à droite en x et A′d (x) = f (x).
Par un raisonnement analogue quand h < 0, on obtient que A est dérivable à gauche et que A′g (x) = f (x).
Conclusion : Comme pour tout x ∈ [a, b] A′d (x) = f (x) = A′g (x),
A est dérivable en tout x ∈ [a, b] et A′ (x) = f (x).
Remarque : A(a) = 0 ; en fait A est l’unique primitive de f sur [a, b] qui s’annule en a.
Théorème
Toute fonction continue sur un intervalle I possède au moins une primitive sur I.
Théorème Soit F une primitive de f sur l’intervalle I.
Alors l’ensemble des primitives de f sur I est l’ensemble des fonctions de la forme F + k où k ∈ R.
Démonstration
Soit k ∈ R et G = F + k, alors G′ = F ′ + 0 = f donc G est bien une primitive de f sur I.
1
Réciproquement, soit G une primitive de f sur I. Alors F − G est dérivable sur I et ∀x ∈ I, (F − G)′ (x) =
F ′ (x) − G′ (x) = f (x) − f (x) = 0 donc la fonction F − G est constante sur I.
Donc, ∃k ∈ R/∀x ∈ I, F (x) − G(x) = k.
Théorème Soit f une fonction continue sur I et x0 ∈ I.
Alors pour tout y0 ∈ R, il existe une unique primitive F de f telle que F (x0 ) = y0 .
Démonstration
L’existence est donnée par le théorème précédent.
Montrons l’unicité : soient deux primitives F et G qui conviennent. On sait qu’il existe k ∈ R, tel que
F = G + k. Mais y0 = F (x0 ) = G(y0 ) + k = y0 + k implique k = 0 et F = G.
Exemples
1. Chercher la primitive sur R de f : x 7→ x + 1 qui s’annule en 1.
2
Une telle primitive est de la forme F : x 7→ x2 + x + k. Or F (1) = 0 ⇔ k = − 23 . D’où l’unique
2
solution : x 7→ x2 + x − 23 .
2. Chercher la primitive sur R∗+ de g : x 7→ x12 + 3 qui s’annule en 2.
11
On trouve la fonction x 7→ −1
x + 3x − 2 .
1.2
Primitives de référence
f (x)
F (x)
xn (n ∈ Z\{−1})
avec n = −2,
1
x2
xα (α ∈ R\{−1})
1
avec α = − 21 , √
x
1
x
ex
u′ (x)(u(x))n (n ∈ Z\{−1})
avec n = −2,
u′
u2
u′ uα (α ∈ R\{−1})
u′
avec α = − 12 : √
u
u′
u
′
u eu
intervalle I
xn+1
+C
n+1
1
− +C
x
xα+1
+C
α+1
√
2 x+C
R si n ≥ 0, R∗+ ou R∗− si n < 0
ln |x| + C
R∗+ ou R∗−
ex + C
(u(x))n+1
+C
n+1
1
− +C
u
uα+1
+C
α+1
√
2 u+C
R∗+ ou R∗−
R∗+
R∗+
R
I ⊂ Du et si n < 0, u ne s’annulant pas
u ne s’annulant pas sur I
u strictement positive sur I
u strictement positive sur I
ln |u| + C
u ne s’annulant pas sur I
eu + C
I ⊂ Du
On fera particulièrement attention à la valeur absolue pour la primitive de x 7→ x1 .
En effet, vérifions que g : x 7→ ln |x| est bien une primitive de x 7→ x1 sur R∗− comme sur R∗+ :
1
1
−1
= ; et si x ∈ R+∗ , g(x) = ln(x) d’où g ′ (x) = .
si x ∈ R−∗ , |x| = −x donc g(x) = ln(−x) et g ′ (x) =
−x
x
x
1.3
Opérations sur les primitives
Proposition
Soient F et G deux fonctions qui sont des primitives respectivement de f et de g et soit λ un nombre réel.
2
1. F + G est une primitive de f + g,
2. λF est une primitive de λf .
Démonstration
Par linéarité de la dérivation (F + g)′ = F ′ + G′ = f + g et (λF )′ = λF ′ = λf .
2
Intégration sur un segment
2.1
Définitions
Définition
Soit f une fonction continue sur [a; b]. On appelle intégrale de a à b de la fonction f le nombre réel
Rb
F (b) − F (a) où F est une primitive quelconque de f et on le note a f (t)dt.
Rb
Par convention, [F (t)]ba = F (b) − F (a) et donc on a l’écriture suivante : a f (t)dt = [F (t)]ba = F (b) − F (a).
R2
3
Exemple : 1 x2 dx = [ x3 ]21 = 83 − 31 = 73 .
Quel résultat aurait-on obtenu si on avait choisi la primitive x →
x3
3
+ 3?
Remarque
Le résultat ne dépend pas de la primitive choisie ; en effet si l’on remplace la primitive F par une primitive
G, on sait qu’il existe k ∈ R tel que G = F +k. Alors on a G(b)−G(a) = F (b)+k−(F (a)+k) = F (b)−F (a).
Théorème
Rx
Soit f une fonction continue sur un intervalle I et x0 ∈ I alors la fonction F : x 7→ x0 f (t)dt est l’unique
primitive de f sur I qui s’annule en x0 . En particulier, F est de classe C 1 sur I et sa dérivée est F ′ = f .
Exemples
.
Rx
1. f : x 7→ x + 1 est continue sur R donc F : x 7→ 1 (t + 1)dt est l’unique primitive de f qui s’annule
2
2
2
2
en 1. Or F (x) = [ t2 + t]x1 = x2 + x − ( 12 + 1) = x2 + x − 23 . On retrouve bien le même résultat !
R x dt
1
est continue sur ]0; +∞[ donc x 7→ 1
est l’unique primitive de f sur ]0, +∞[ qui
2. f : x 7→
x
t
1
s’annule en 1 : on la note ln. On obtient que ln est de classe C 1 sur ]0; +∞[ et (ln x)′ = .
x
2.2
Interprétation graphique
Exemple : soit f la fonction définie sur [0, 1] par f (x) =R −3x + 3.
1
Alors une primitive de f est F (x) = − 32 x2 + 3x. Donc 0 f (t)dt = F (1) − F (0) = 3 − 3/2 = 3/2.
Représenter la fonction et calculer l’aire du triangle délimité par la
courbe de f sur [0, 1] et les deux axes : on obtient 3/2.
Maintenant,
considèrons la fonction f sur [0, 3] :
R3
f
(t)dt
=
F
(3) − F (0) = −3/2 ∗ 9 + 3 ∗ 3 = −9/2.
0
Si on calcule l’aire des deux triangles du dessin : on obtient 3/2 et 6 ; on
remarque alors que 3/2 − 6 = −9/2.
3
1
3
0
1
C_f
Rb
Plus généralement, si a < b, a f (t)dt représente l’aire signée du domaine délimité par C (courbe
représentative de f dans un repère orthonormé), l’axe des abscisses et les droites d’équations x = a
et x = b.
3
a
2.3
2.3.1
b
Propriétés générales de l’intégrale
Premières propriétés
Soit f une fonction continue sur un segment [a, b].
Les propriétés suivantes découlent de la définition de l’intégrale :
Z
Z b
Z a
f (t)dt = −
f (t)dt = 0
a
a
a
f (t)dt
b
Ra
En effet, si F est une primitive de f , on sait que a f (t)dt = F (a) − F (a) = 0 et
Ra
Rb
f
(t)dt
=
F
(a)
−
F
(b)
=
−(F
(b)
−
F
(a))
=
−
b
a f (t)dt.
2.3.2
Relation de Chasles
Proposition
Soit f une fonction continue sur I et soit a, b, c trois éléments de I alors on a
Z b
Z c
Z b
f (t)dt
f (t)dt +
f (t)dt =
2.3.3
c
a
a
Linéarité de l’intégrale
Proposition
Soient f et g deux fonctions continues sur un segment [a, b] et λ ∈ R : alors
Z b
Z b
Z b
Z b
Z b
f (t)dt.
λf (t)dt = λ
g(t)dt
et
f (t)dt +
(f (t) + g(t))dt =
a
2.3.4
a
a
a
a
Positivité et inégalités
Proposition
Soient f et g deux fonctions continues sur un segment [a, b] avec
Rb
1. Si ∀t ∈ [a; b] f (t) ≥ 0 alors a f (t)dt ≥ 0
Rb
Rb
2. Si ∀t ∈ [a; b] f (t) ≥ g(t) alors a f (t)dt ≥ a g(t)dt
a ≤ b.
Remarque
Cette proposition signifie que l’on peut intégrer des inégalités, à condition que les bornes de l’intégrale
soient dans le bon sens : graphiquement, l’intégrale étant représentée par une aire, cette proposition est
évidente.
Attention,
siR les bornes sont
Ra
R bdans le mauvais
R b sens, tout
R b devient faux
R b car
a
f
(t)dt
≥
g(t)dt
⇔
−
f
(t)dt
≥
−
g(t)dt
⇔
f
(t)dt
≤
b
b
a
a
a
a g(t)dt !
Démonstration 1.
Soit F une primitive de f . Alors F est dérivable et F ′ = f ≥ 0 par hypothèse, donc F est croissante.
4
On en déduit que
Rb
a
f (t)dt = F (b) − F (a) ≥ 0 si a ≤ b.
Proposition
Soit f une fonction continue sur [a, b].
Rb
Si ∀t ∈ [a; b] f (t) ≥ 0 et a f (t)dt = 0 alors f (t) = 0 pour tout t ∈ [a; b].
5
Proposition
Soit f une fonction continue sur [a, b]
R
R
b
b
1. Inégalité triangulaire : a f (t)dt ≤ a |f (t)| dt
2. Inégalité de la moyenne : soient m et M deux réels tels que pour tout t ∈ [a, b] m ≤ f (t) ≤ M .
1 Rb
f (t)dt ≤ M .
Alors m ≤
b−a a
Démonstration
2. on sait : ∀t ∈ [a, b], m ≤ f (t) ≤ M donc par la proposition précédente, comme a ≤ b :
Rb
Rb
Rb
Rb
≤ a M dt. Or a mdt = [mt]ba = mb − ma = m(b − a).
a mdt ≤ a f (t)dt
Rb
D’où m(b − a) ≤ a f (t)dt ≤ M (b − a). On conclut en divisant par b − a > 0.
3
3.1
Méthodes de calcul des intégrales
Méthode directe
Dès que l’on connait une primitive de la fonction à intégrer, on peut calculer l’intégrale en utilisant la
définition.
√
√
√
R 2 tdt
= [ t2 + 1]21 = 5 − 2.
Exemple : 1 √
2
t +1
3.2
Intégration par partie
Théorème
Soient u et v deux fonctions C 1 sur [a; b] alors
Z
b
′
u (t)v(t)dt =
a
[u(t)v(t)]ba
−
Z
b
u(t)v ′ (t)dt
a
Démonstration
En effet, si u et v sont deux fonctions C 1 sur [a, b] alors uv est C 1 sur [a, b] et (uv)′ (t) = u′ (t)v(t)+u(t)v ′ (t).
Rb
Rb
Rb
Rb
D’où a (uv)′ (t)dt = a (u′ (t)v(t) + u(t)v ′ (t))dt = a u′ (t)v(t)dt + a u(t)v ′ (t)dt. On conclut en remarquant
Rb
que a (uv)′ (t)dt = [u(t)v(t)]ba .
Exemple important : calcul d’une primitive de la fonction ln
sur R∗+ .
R
x
La fonction ln étant continue sur R+∗ , la fonction x 7→ 1 ln(t)dt en est une primitive (c’est l’unique
primitive qui s’annule en 1). Calculons cette intégrale via une intégration par parties en posant :
′
u′ (t) = 1 et v(t) = ln(t). Alors
= 1tR. Les fonctions u et v sont de classe C 1 sur l’intervalle
R x u(t) = t et v (t)
x
[1, x], pour x > 0, donc : 1 ln(t)dt = [t ln(t)]x1 − 1 dt = x ln(x) − x + 1.
Les primitives sur R∗+ de la fonction x 7→ ln(x) sont donc les fonctions x 7→ x ln(x) − x + C où C ∈ R.
3.3
Changement de variable
Théorème
Soit f une fonction continue sur [a; b] et u une fonction C 1 sur [α; β] telle que u([α; β]) ⊂ [a; b]. Alors
Z
β
′
f (u(t))u (t)dt =
α
Z
u(β)
f (x)dx
u(α)
Attention : Penser à changer les bornes d’intégration !
Changement de variable : on a posé x = u(t), alors dx = u′ (t)dt et t = α ⇒ x = u(α) et t = β ⇒ x = u(β).
Démonstration
Toutes les fonctions sont continues donc les intégrales ont bien un sens.
Soit F une primitive de f et G = F ◦ u ; alors F et G sont de classe C 1 et
6
G′ (x) = F ′ (u(x))u′ (x) = f (u(x))u′ (x).
Rβ
Rβ
R u(β)
D’où α f (u(t))u′ (t)dt = α G′ (t)dt = G(β) − G(α) = F (u(β)) − F (u(α)) = u(α) f (x)dx.
Exemples :
R2
1. Calcul de I = 1 3t22t+1 dt. On effectue le changement de variable x = t2 (= u(t)).
Alors dx = 2t dt = (u′ (t)dt) et les bornes deviennent : t = 1 ⇒ x = 12 = 1 et t = 2 ⇒ x = 22 = 4.
R4 1
D’où I = 1 3x+1
dx = 13 [ln |3x + 1|]41 = ln(13)−ln(4)
.
3
R 1 et
t
2. Calcul de I = 0 1+e
−t dt en posant x = e .
t
AlorsR dx = e dt
: t = 0 ⇒ x = e0 = 1 et t = 1 ⇒ x = e1 = e. d’où
R e etx les bornes
R e deviennent
e dx
1
I = 1 1+1/x = 1 x+1 dx = 1 1 − x+1
dx = [x − ln |x + 1|]e1 = e − ln(e + 1) − 1 + ln(2).
R 0 dx
3. Transformation de J = −2 1+x
2 en posant x = −t. Alors dx = −dt, et les bornes deviennent :
x = −2
⇒
t
=
2
et
x
=
0
⇒
t
=
0.
En
R 0 −dt
R 2 −dt
R 2 dt utilisant
R 2 dx maintenant l’égalité de la droite vers la gauche, on obtient
J = 2 1+(−t)
=
−
=
=
2
0 1+t2
0 1+t2
0 1+x2 !
Soit f une fonction continue sur [−a; a].
Ra
Ra
1. Si f est paire sur [−a; a] alors −a f (t)dt = 2 0 f (t)dt.
Ra
2. Si f est impaire sur [−a; a] alors −a f (t)dt = 0.
Proposition
Démonstration
Cette proposition se visualise très bien graphiquementRavec des considérations
d’aire.
R a Sinon, par le calcul :
R0
a
1. Supposons f paire. D’après la relation de Chasles, −a f (t)dt = −a f (t)dt + 0 f (t)dt.
Dans la première intégrale,
; alors dt = −du et t = 0 ⇒ u = 0,
R a variable t = R−u
R 0 le changement de
R 0 on effectue
a
t = −a ⇒ u = a d’où −a f (t)dt = a f (−u)(−du) = 0 f (−u)du = 0 f (u)du car f est paire.
4
Fonctions définies par une intégrale
Dans cette section, le but n’est plus de calculer des intégrales, mais d’obtenir des propriétés sur des
fonctions définies par une intégrale. L’étude sera faite intégralement dans les exercices, mais le point
méthode est le suivant :
Repérer de quel type est la fonction définie par une intégrale en jeu. Il y en a deux :
F : x 7→
Z
x
f (t)dt
ou
cste
G : x 7→
Z
v(x)
f (t)dt.
u(x)
Dans le cas du premier type : étudier la continuité de f , pour en déduire que la fonction F est l’unique
primitive de f sur ... et qui s’annule en cste.
Le deuxième type est plus difficile : étudier la continuité de f sur ... . Alors, on sait qu’il existe une
v(x)
primitive de f sur ... : on la note F . On obtient que G(x) = [F (t)]u(x) = F (v(x)) − F (u(x)) ; on peut alors
poursuivre en utilisant les propriétés de F : F étant une primitive de f sur ..., F est dérivable, même C 1 sur
... et F ′ = f d’où par composition, G est dérivable, même C 1 et G′ (x) = v ′ (x)F ′ (v(x))−u′ (x)F ′ (u(x)) = ...
5
5.1
Sommes de Riemann
Convergence des sommes de Riemann
Exemple :
On considère la fonction f définie sur [0, 1] par f (x) = x2 .
k
k 2
Méthode des rectangles : on considère les rectangles de base [ nk , k+1
n ] et de hauteur f ( n ) = ( n ) ainsi que
k+1 2
k+1
ceux de hauteur f ( n ) = ( n ) pour tout k ∈ [[0, n − 1]].
7
1
On note Sn la somme des aires des
petits rectangles , et Sn′ la somme
des aires des grands rectangles.
0
k/n
1=n/n
On va vérifier que si n est suffisamment
grand, la somme des aires de ces rectangles forment un encaR1
drement assez précis de la valeur de 0 x2 dx = 1/3.
n−1
n−1
n−1
P k+1 k
P1 k 2
1 P 2
( n − n ) × ( nk )2 =
Sn =
(
)
=
k = (n−1)n(2(n−1)+1
= (n−1)(2n−1)
.
3
n n
n
6n3
6n2
k=0
k=0
k=0
n
P
n
1 k 2
k
k+1 2
1 P 2
−
)
×
(
)
=
(
)
=
k = (n+1)(2n+1)
.
( k+1
3
n
n
n
n n
n
6n2
k=1
k=1
k=0
R1 2
1
6n
′
On remarque que Sn ≤ 0 x ≤ Sn′ et Sn′ −Sn = 6n
2 = n ; donc Sn (ou Sn ) est une bonne valeur approchée
de l’intégrale de f .
R1
En particulier, il est facile de montrer que lim Sn = 1/3 = lim Sn′ (et 1/3 = 0 x2 dx !).
et de même Sn′ =
n−1
P
n→+∞
n→+∞
Définition
Soit f une fonction continue sur [a; b] et n un nombre entier strictement positif. On appelle sommes de
Riemann de f sur [a; b] les expressions
n−1
Sn (f ) =
n
b−aX
b−a
f (a + k
)
n
n
et
Sn′ (f ) =
k=0
b−a
b−aX
f (a + k
)
n
n
k=1
Ce nombre est en fait la somme des aires des rectangles associés à la courbe de f .
C(f)
S_n(f) = somme des aires des petits rectangles
S’_n(f) = somme des aires des grands rectangles
b
a
subdvision régulière du segment [a,b] en n morceaux
En particulier si a = 0 et b = 1 :
Sn (f ) =
P k
1 n−1
f( )
n k=0 n
et
Sn′ (f ) =
n
k
1 P
f( )
n k=1 n
Le résultat que l’on a obtenu dans l’exemple se généralise :
Théorème
Soit f une fonction continue sur [a; b] alors les suites (Sn (f ))n>1 et (Sn′ (f ))n>1 convergent et
lim Sn (f ) =
n→+∞
Z
b
a
f (t)dt = lim Sn′ (f )
n→+∞
Remarque
Rb
On déduit de ce théorème que Sn (f ) est une bonne approximation (valeur approchée) de a f (t)dt dès
que n est suffisamment grand.
8
Démonstration
Par souci de simplification, on va démontrer ce résultat dans le cas où f est monotone, par exemple croisR1
P k
1 n−1
f ( ) = 0 f (t)dt.
sante, avec a = 0 et b = 1. Il nous faut donc montrer que lim
n→+∞ n k=0
n
Fixons n ∈ N, et soit k ∈ [[0, n − 1]]. Par croissance de f , ∀t ∈ [ nk , k+1
],
f ( nk ) ≤ f (t) ≤ f ( k+1
n
n ) et donc
R
k+1/n
k
1
k+1
d’après l’inégalité de la moyenne, f ( n ) ≤ k+1 − k k/n f (t)dt ≤ f ( n )
n
n
R k+1/n
).
En
sommant
ces inégalités pour k variant de 0 à n − 1, on obtient
soit n1 f ( nk ) ≤ k/n f (t)dt ≤ n1 f ( k+1
n
n−1
n−1
n−1
n
R
P k+1/n
P k+1
P k
1 P
f (t)dt ≤ n1
f ( nk ) ≤
f ( n ) = n1
f ( n ).
n
k/n
k=0
k=0
k=1
R 1 k=0
Relation de Chasles : Sn (f ) ≤ 0 f (t)dt ≤ Sn (f ) − f (0)/n + f (1)/n.
R1
R1
f (0) − f (1)
D’où l’encadrement : 0 f (t)dt +
≤ Sn (f ) ≤ 0 f (t)dt.
n
On conclut à l’aide du théorème d’encadrement.
5.2
Application à la convergence de certaines suites : exemple
P 3
P k 3 1 − 0 n−1
P
1 n−1
k
1 n−1
k
.
Alors
u
=
( ) =
(0 + (1 − 0) × )3 .
n
4
n k=0
n k=0 n
n k=0
n
Ainsi un est la nème somme de Riemann de la fonction f définie par f (x) = x3 , qui est continue sur [0; 1].
R1
1
Donc lim un = x3 dx = .
n→+∞
4
0
Soit un =
9