TS1 Planètes et satellites Page 1 sur 3 4 T r GM π =

TS1
Planètes et satellites
Exercice 1. : La planète MARS.
Spirit creuse, Opportunity avance :
Les deux robots sont à la tâche sur la planète Mars.
Le premier a prélevé un morceau de caillou.
«Comme des myrtilles sur un muffin»: telle est la roche étudiée par le second.
(Extrait du journal Libération mardi 10 février 2004)
Données : masse du Soleil, MS = 2,0.10 kg ; masse de Mars, MM = 6,5.1023 kg ;
rayon de Mars, RM = 3 400 km ; période de révolution de Mars, TM = 687 jours ;
G = 6,6710-11 N.kg-2.m2.
Le centre d'inertie de la planète Mars décrit autour du Soleil une orbite circulaire de rayon r à la vitesse constante
v. On admet que la planète Mars et le Soleil ont une répartition de masse à symétrie sphérique. On note TM la
période de révolution de la planète Mars autour du Soleil.
1.
a. Préciser par rapport à quel référentiel le mouvement de Mars est ainsi décrit.
b. Exprimer la valeur a de l’accélération du centre d'inertie de Mars en fonction de v et de r, puis de r et de
TM.
c. Exprimer la valeur de la force F que le Soleil exerce sur Mars en fonction de G, r, MS et MM.
30
d. En appliquant la deuxième loi de Newton à la planète Mars, montrer que :
TM2
4π 2
(expression de
=
r 3 GM S
la troisième loi de Kepler).
e. Déduire, des relations précédentes et des données, les valeurs numériques de r, F, v et a.
2. Le robot Spirit a mesuré, à la surface de Mars, le poids d'un caillou de masse m = 100 g. Il a trouvé
0,38 N.
Quelle est la valeur du champ de gravitation gM sur Mars ? En assimilant force gravitationnelle et poids à
la surface de Mars, montrer que cette valeur est celle que prévoit la loi de gravitation universelle.
Exercice n°2 L'Univers dans la balance.
«On sait que l'étude du mouvement de chute d'un objet de masse m, soumis à l'attraction gravitationnelle
d'un astre de masse M, permet de déterminer cette masse M, si l'on a au préalable déterminé la valeur de
la constante de gravitation universelle G. Mais, en dehors de notre planète, l'expérience n'est guère
réalisable! Heureusement, un exemple de chute est fourni par un satellite ; s'il ne tombe pas, c'est parce
que la vitesse initiale, qui lui a été communiquée perpendiculairement à la verticale, le tient éloigné de la
planète qui l’attire. Son mouvement suit la troisième loi de Kepler qui indique que : T² = Cte.
a3
La constante fait intervenir les facteurs G et M. Ainsi, connaissant G, la mesure de a et de T permet de
déterminer M. On a réalisé une véritable balance cosmique!»
Extrait de l'article L'Univers dans la balance, paru dans une revue scientifique en 1995.
Le but de cet exercice est de vérifier l'exactitude de l'article et d'utiliser les relations mentionnées pour
déterminer la masse de certains corps célestes. Toutes les orbites sont considérées comme circulaires.
Données :
Constante de gravitation universelle G = 6,67 10-11 N.m² kg-²
Rayon de l'orbite et période de révolution :
satellite
Rayon de
l'orbite (m)
Période de
révolution (s)
Jupiter (soleil)
rJ = 7,78×1011
TJ = 3,74×108
Io ( Jupiter)
rIo = 4,22×108
TIo = 1,53×105
Lune (Terre)
rL = 3,84×108
TL = 2,36×106
Page 1 sur 3
TS1
Planètes et satellites
Étude préliminaire.
La valeur de la force gravitationnelle exercée par un astre de masse M à symétrie sphérique sur un corps
de masse m également à symétrie sphérique a pour expression :
f = G Mm
r²
Que représente r dans l'expression précédente ?
L'astre de masse M est-il soumis à une force ? Si oui, indiquer ses caractéristiques et faire un schéma.
Dans la suite de l'exercice, tous les corps étudiés seront à symétrie sphérique et pourront être assimilés à
des objets ponctuels.
On considère un satellite de masse m soumis à l'attraction gravitationnelle d'un astre de masse M. On
suppose que le mouvement de révolution du satellite est un mouvement circulaire uniforme de rayon r.
Préciser les caractéristiques du vecteur accélération du satellite dans le référentiel lié à l’astre. (on pourra
faire un schéma).
Montrer que le mouvement circulaire uniforme est solution de la deuxième loi de Newton appliquée au
satellite.
En déduire que la valeur de la vitesse constante du satellite a pour expression :
v=
GM
r
Dans l'hypothèse où la masse du satellite est différente de m, par exemple m' = 3m, indiquer, en le
justifiant, si la vitesse est modifiée ou non.
Montrer que la troisième loi de Kepler est bien vérifiée et donner l'expression de la constante à laquelle
l'auteur fait allusion dans le texte.
Applications de la troisième loi de Kepler.
En utilisant les données relatives au mouvement de la Lune par rapport à la Terre, calculer, à partir de la
troisième loi de Kepler, la valeur de la masse MT de la Terre.
Par analogie avec le calcul précédent, déterminer la valeur de la masse MJ de Jupiter.
Par analogie avec le calcul précédent, déterminer la valeur de la masse MS du Soleil.
Exercice 3 : Satellites de Jupiter.
Galilée commença à observer la planète Jupiter en janvier 1610 avec une lunette de sa fabrication.
Il découvrit qu’autour de Jupiter tournaient «quatre lunes», auxquelles il donna le nom d’astres médicéens ; ce
sont quatre satellites de Jupiter : Io, Europe, Ganymède et Callisto.
Partie I
1.
a) Représenter sur un schéma la force de gravitation FJ/E exercée par Jupiter sur Europe, et celle FE/J
exercée par Europe sur Jupiter.
b) Donner l’expression vectorielle de FJ/E, les centres des deux astres étant séparés d’une distance d.
2.
a) Le mouvement du satellite Europe (noté E) est étudié dans le référentiel «jupitocentrique». Par analogie
avec le référentiel géocentrique, donner les caractéristiques d’un référentiel « jupitocentrique ».
b) On modélise le mouvement du centre d’inertie du satellite Europe par un mouvement circulaire
uniforme.
E2
E1
J
Sens de
rotation
du satellite
sur son orbite
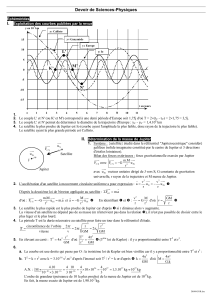
• Comparer les vecteurs vitesse V1 et V2 et accélération a 1 et a 2 du
satellite aux points E1 et E2.
• Reproduire le schéma ci-après et y tracer ces vecteurs (avec les
mêmes échelles en E1 et E2).
Page 2 sur 3
TS1
Planètes et satellites
Partie II.
1.
2.
3.
Établir que la valeur de la vitesse d’un satellite de Jupiter est telle que: V2 = GMJ où r désigne le rayon de
r
l’orbite du satellite.
En déduire l’expression de la période T de révolution du satellite en fonction de G, MJ et r.
2
a) Montrer que le rapport T3 est constant pour les différents satellites de Jupiter
r
b) La période de révolution de le autour de Jupiter est TIo = 1 j 18 h 18 min. Thébé, un autre satellite de
Jupiter, possède une orbite de rayon moitié de celui de l’orbite de Io. Déterminer la période de révolution
Tth de Thébé autour de Jupiter.
4. Thébé est-il un satellite « jupitostationnaire » ? Justifier sans calcul la réponse sachant que la période de
rotation propre de Jupiter est TJ = 9 h 55 min.
Page 3 sur 3