Leçon 30 : groupes du parallélogramme, du rectangle, etc.

Leçon 30 : groupes du parallélogramme,
du rectangle, etc.
Université Claude Bernard–Lyon I
CAPES de Mathématiques : Oral
Année 2005–2006
Difficultés de la leçon
• D’abord, donner une définition opérationnelle d’un parallélogramme, d’un rectangle, etc. :
ensemble de 4 points, ensemble de 4 segments, réunion de 4 segments (i.e. un seul ensemble de points), ou enveloppe convexe des sommets ? Quelle que soit la définition, il
faut savoir qu’une isométrie préserve les sommets, le centre de gravité, les côtés et les
diagonales.
• D’autre part, il faut une démarche pour déterminer le groupe des isométries.
– Pour rechercher les isométries positives, on cherche des contraintes.
– On n’oublie pas de vérifier que les isométries candidates conviennent.
– Le lemme 2◦ (a) est bien utile pour limiter les études de cas.
0◦ Prérequis
On fixe un plan affine euclidien. On suppose connaı̂tre :
• quelques notions de base sur les groupes,
• quelques notions de base sur les plans affines euclidiens,
• en particulier, ses isométries (classification des isométries ayant un point fixe).
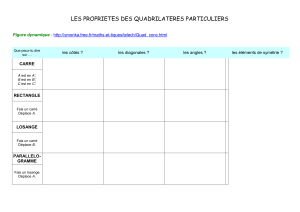
1◦ Parallélogrammes
(a) Stratégie recommandée
Il faut donner une définition des parallélogrammes et s’y tenir : si on définit un parallélogramme
comme un ensemble formé de quatre segments (voir la leçon “polygones réguliers”), il faut
alors démontrer qu’une isométrie qui conserve le parallélogramme conserve l’ensemble de ses
sommets.
Dans cette leçon-ci, je conseille de définir un parallélogramme comme un ensemble non ordonné
de quatre points. Concrètement, je conseille de dire les choses suivantes :
1. On définit un parallélogramme par [définition ci-dessous].
2. On peut alors définir les diagonales comme les segments qui contiennent le centre de
gravité, et les côtés.
3. Une isométrie f conserve un parallélogramme P si f (P) = P. Les isométries qui conservent P forment un groupe.
4. Comme une isométrie est affine, si f (P) = P, alors f fixe le centre de gravité de P. Par
la même propriété, elle envoie une diagonale sur une diagonale, et, par complément, un
côté sur un côté.
Les détails, fort pesants, suivent. Savoir répondre à une question du jury là-dessus...
(b) Parallélogrammes
Définition On appelle parallélogramme non plat une partie P du plan formée de quatre points,
telle qu’il existe une bijection
φ : {1, 2, 3, 4} −→ P
i
7−→ Ai
−→
−→
−→
−→
satisfaisant : A1 A2 =A4 A3 et A1 A2 , A1 A3 non colinéaires.
1
Attention ! Avec des polygones moins réguliers que les parallélogrammes, cette définition
n’est pas opérationnelle. Voir la “flèche”, le quadrilatère non convexe de G. Chevalier.
Convention Si P est un parallélogramme non aplati et si φ est comme dans la définition,
−→
−→
i.e. P = {A3 , A4 , A2 , A1 } et A1 A2 =A4 A3 , on notera P = A1 A2 A3 A4 .
Remarque Si P est un parallélogramme non aplati, il y a 8 applications φ comme dans la
définition. Si on représente φ par la suite ordonnée (A1 , A2 , A3 , A4 ), ou plus simplement, 1234,
les autres sont 2341, 3412, 4123, 4321, 3214, 2143, 1432.
Il y a donc 8 façons de noter un parallélogramme {A3 , A4 , A2 , A1 } selon la convention.
(c) Côtés et diagonales
Lemme Si P est un parallélogramme non aplati, le centre de gravité de P est le milieu
d’exactement deux segments ayant pour extrêmités des éléments de P.
Définition On appelle segment porté par une partie, tout segment dont les extrêmités appartiennent à la partie. Parmi les segments portés par un parallélogramme, les deux segments du
lemme sont appelés diagonales, les autres sont appelés côtés.
−→
−→
−→
Démonstration. Soit φ comme dans la définition. L’égalité A1 A2 =A4 A3 = − A3 A4 permet
de montrer que les milieux O de [A1 A3 ] et O0 de [A2 A4 ] coı̈ncident.1 Par associativité du
barycentre, le point O = O0 est le centre de gravité de P.
Pour montrer la deuxième partie, il suffit de vérifier que les 4 segments portés par P autres
que [A1 A3 ] et [A2 A4 ] ne contiennent pas O. Ici, on utilise le fait que P n’est pas aplati.
(d) Conservation d’un parallélogramme - propriétés de base
Définition Pour P une partie du plan, on dit qu’une application f conserve P si f (P) ⊂ P .
Lemme L’ensemble des isométries qui conservent une partie P est un sous-groupe du groupe
des isométries. Si f est une isométrie qui conserve P et P est fini, on a : f (P) = P.
Démonstration. Test du sous-groupe, injectivité des isométries, bijectivité d’une injection
d’un ensemble fini dans lui-même.
Proposition Soit P un parallélogramme non aplati et f une application affine bijective qui
conserve P. Alors f fixe le centre de gravité de P, envoie une diagonale de P sur une diagonale
et un côté sur un côté.
Démonstration. Par hypothèse, f induit une bijection sur l’ensemble fini P. Puisque f est
affine, elle préserve le barycentre. En particulier, O est fixé par f et l’image d’un segment porté
par P est porté par P. Le milieu de l’image d’une diagonale est l’image du milieu, donc c’est
O, donc l’image d’une diagonale est une diagonale. Par suite, l’image d’un côté est un côté.
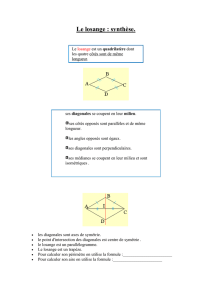
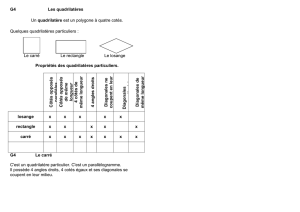
(e) Parallélogrammes particuliers
Définition Un parallélogramme non aplati est un rectangle (resp. un losange) si ses côtés
consécutifs (ayant un point commun) sont perpendiculaires (resp. isométriques). C’est un carré
si c’est un rectangle et un losange.
Proposition Un parallélogramme non aplati est
(i) un rectangle si et seulement si ses diagonales sont isométriques.
(ii) un losange si et seulement si ses diagonales sont perpendiculaires.
1
−→
−→
−→
−→
−→
−→
A1 A4 =A1 A2 + A2 A3 + A3 A4 =A2 A3 , puis, A1 O=
1
2
2
−→
A1 A3 =
1
2
−→
−→
A1 A4 + 21 A4 A3 =
1
2
−→
−→
−→
A1 A4 + 12 A1 A2 =A1 O0 .
Démonstration. (i) Un triangle est rectangle SSI il est inscrit dans un demi-cercle.
(ii) La médiatrice d’un segment est d’une part l’ensemble des points équidistants des extrêmités
du segment, d’autre part la droite perpendiculaire au segment qui contient son milieu.
Remarque Il y a une dualité entre “le” rectangle et “le” losange, qu’on utilisera plus tard :
segments
rectangle
losange
côtés
perpendiculaires
isométriques
diagonales
isométriques
perpendiculaires
2◦ Deux lemmes triviaux mais utiles (le premier plus que l’autre)
(a) Isométries directes et indirectes
Lemme Soit G un sous-groupe du groupe des isométries du plan, G+ le sous-groupe de G
formé des isométries de déterminant 1. Si G \ G+ contient un élément s, les applications
f 7→ s ◦ f et f 7→ s−1 ◦ f sont des bijections réciproques entre G+ et G \ G+ .
Utilisation : si on connaı̂t G+ et card(G+ ) éléments de G \ G+ , on connaı̂t donc G entier.
(b) Cas de figures semblables
Lemme Soit P et P 0 deux parties finies du plan, et h une similitude qui envoie bijectivement
P sur P 0 . Alors l’application
f 7→ hf h−1
est un isomorphisme du groupe des isométries de P sur celui de P 0 .
3◦ Groupe des isométries d’un parallélogramme
(a) Soit P = ABCD un parallélogramme non aplati qui n’est ni un losange, ni un rectangle.
Une isométrie qui conserve P fixe le centre de gravité O de P. C’est donc une rotation de
centre O ou une réflexion d’axe contenant O.
(b) Une isométrie qui fixe O envoie A sur A0 ∈ {A, B, C, D} tel que OA = OA0 . Or, puisque
P n’est pas un rectangle, OA 6= OB et OA 6= OD. Donc A0 est A ou C.
(c) Comme une rotation est déterminée par son centre et l’image d’un point, une rotation qui
conserve P est l’identité ou la symétrie de centre O.
Inversement, comme les diagonales de P se coupent en O, la symétrie de centre O conserve P.
(d) Supposons qu’il existe une réflexion qui conserve P. Si A est fixe, l’axe de la réflexion est
(OA) = (AC), donc C est fixe. Par complément, B et D sont permutés. Comme B et D ne
sont pas sur (AC), c’est que (BD) est perpendiculaire à l’axe de la réflexion, donc que P est
un losange. Contradiction.
(e) Ainsi, le groupe d’un parallélogramme qui n’est ni rectangle ni un losange contient l’identité
et la symétrie centrée au centre de gravité. Il est isomorphe à Z/2Z.
4◦ Groupe des isométries d’un losange et d’un rectangle
(a) Soit L = ABCD un losange qui n’est pas un rectangle. Les arguments de (a), (b) et (c)
ci-dessus s’appliquent encore, donc le groupe des rotations qui conservent L le groupe formé
par l’identité et la symétrie sO de centre O.
(b) La caractérisation de la médiatrice permet de vérifier que les deux réflexions s1 et s2 d’axes
les diagonales conservent le losange.
(c) Par le lemme utile 2◦ (a), le groupe des isométries qui conservent L est de cardinal 4.
(d) On constate que les trois éléments non triviaux de ce groupe sont d’ordre 2, ce qui permet
d’affirmer qu’il est isomorphe à Z/2Z×Z/2Z. On peut aussi donner un isomorphisme explicite :
s1 7→ (1, 0), s2 7→ (0, 1), sO 7→ (1, 1).
3
(e) Soit à présent R = IJKL un rectangle qui n’est pas un losange. On pourrait s’en tirer
avec des arguments analogues à ceux qui précèdent, mais on va procéder différemment.
Soit A, B, C, D les milieux de [IJ], [JK], [KL], [LI]. Avec 1◦ (e), on vérifie que ABCD est
un losange. Par conservation du milieu, si une isométrie conserve R, elle conserve ABCD.
A présent, soit I 0 , J 0 , K 0 , L0 les milieux de [AB], [BC], [CD], [DA]. Comme ci-dessus, si une
isométrie conserve ABCD, elle conserve I 0 J 0 K 0 L0 .
(f ) Or, on vérifie sans peine que l’homothétie h de centre O, centre de gravité de R, et de
rapport 1/2, envoie R sur R0 = I 0 J 0 K 0 L0 . Comme h commute à toute isométrie du plan qui fixe
O, l’isomorphisme de 2◦ (b) est l’identité : les groupes de R et de R0 coı̈ncident. Les inclusions
de (e) montrent que c’est aussi celui de L.
Au bilan, le groupe des isométries de R est le groupe d’ordre 4 engendré par les réflexions
d’axes les médiatrices des côtés, qui sont les diagonales de L.
(g) Je ne sais pas expliquer a priori que tous les rectangles ont le même groupe de symétrie.
5◦ Groupe des isométries d’un carré
(a) Soit C = ABCD un carré, O son centre de gravité. Une isométrie directe qui conserve C est
une rotation de centre O. Elle est parfaitement déterminée par l’image d’un point, par exemple
A, laquelle peut prendre 4 valeurs possibles. Il y a donc au plus 4 rotations qui conservent C.
Or, les rotations d’angles 0, ±π/2 et π conservent C, car les diagonales de C sont orthogonales
et de même longueur. Par suite, il y a exactement 4 rotations qui conservent C.
(b) Les 4 réflexions d’axes les diagonales et les médiatrices des côtés conservent C, car C est
un losange et un rectangle. Par le lemme utile de 2◦ (a), on a fait le tour de ces choses.
(c) Le groupe des isométries qui conservent C est donc d’ordre 8. On l’appelle groupe diédral.
On montre qu’il est engendré par une rotation r d’angle ±π/2 et une réflexion s. On vérifie
qu’il n’est pas commutatif : srs−1 = r −1 . Il contient un sous-groupe distingué, isomorphe à
Z/4Z (les rotations) et le quotient est isomorphe à Z/2Z.
(d) Le lemme 2◦ (b) donne une bonne raison a priori pour laquelle tous les carrés ont le même
groupe d’isométries, car tous les carrés sont semblables.
6◦ Compléments
(a) On peut savoir qu’il y a un seul autre groupe non abélien de cardinal 8, qu’on décrit par :
Q = {±1, ±i, ±j, ±k}, où le produit est déterminé par : 1 est neutre, (−1) commute à tout le
monde ((−1)i = i(−1) = −i, etc.), i2 = j 2 = k2 = −1, ij = −ji = k.
Le groupe du carré et le groupe Q ne sont pas isomorphes, car le groupe du carré contient 2
éléments d’ordre 4 (r et r 3 ), alors que Q en contient 6 (±i, ±j et ±k).
(b) Montrons a priori que le groupe de n’importe quel rectangle s’injecte dans celui du carré.
Fixons une affinité a de rapport convenable qui transforme notre rectangle ABCD en un carré
A0 B 0 C 0 D 0 . Considérons alors l’application f 7→ af a−1 définie sur l’ensemble des applications
affines du plan. Si f conserve le rectangle, alors af a−1 préserve les sommets du carré, comme
dans le lemme 2◦ (b).
Or, toute application affine bijective qui préserve le carré est une isométrie, ce que l’on peut
−→
−→
vérifier par exemple en considérant l’image du repère (O0 , O0 A0 , O0 B 0 ) (où, bien sûr, O0 est le
centre du carré A0 B 0 C 0 D 0 ). L’application f 7→ af a−1 induit donc une injection des applications
affines qui préservent un rectangle dans le groupe des isométries du carré.
(c) L’intérêt du point (b), c’est de fournir un traitement de la leçon en sens inverse : du carré
vers les parallélogrammes plus généraux.
En effet, connaissant le groupe du carré, il est facile de tester, pour g isométrie du carré, si
a−1 ga est une isométrie du rectangle. Plus généralement, cette méthode marche pour n’importe
quel parallélogramme.
(d) Noter que le groupe du carré décrit aussi les façons de numéroter les parallélogrammes
(voir 1◦ (b)). Pouvez-vous l’expliquer à l’aide de (b) ?
4
C
K
L
B
D
I
A
J