FLMA O99 - Fiche de cours numéro 1: Logique et Ensembles

FLMA O99 - Fiche de cours num´ero 1: Logique et
Ensembles
Laurent Guieu
5 F´evrier 2008
Contents
1 Quelques ´el´ements de logique math´ematique 2
1.1 Propositionslogiques........................... 2
1.2 Exemples ................................. 2
1.3 Connecteurslogiques ........................... 3
1.4 Fauximpliquevrai? ........................... 5
1.5 Formes propositionnelles tautologiques . . . . . . . . . . . . . . . . . 5
1.6 Propositions quantifi´ees . . . . . . . . . . . . . . . . . . . . . . . . . 6
2 Ensembles : Vocabulaire et technologie 7
2.1 Notionsprimitives ............................ 7
2.2 D´efinitions fondamentales . . . . . . . . . . . . . . . . . . . . . . . . 7
2.3 Propri´et´es ................................. 10
1

1 Quelques ´el´ements de logique math´ematique
1.1 Propositions logiques
Une proposition logique est un ´enon¸c´e, not´e par exemple P, auquel il est possible
d’attribuer :
1. soit la valeur “vrai” : on notera alors ν(P) = V;
2. soit la valeur “faux” : on notera alors ν(P) = F.
En logique math´ematique classique, on exige qu’il n’y ait pas de troisi`eme possiblit´e
: c’est le principe du tiers exclus1. La notation ν(P) se lit : “valeur de v´erit´e de P”.
Une proposition logique d´ependant d’un param`etre est une expression du type P(x),
o`u xest une variable, v´erifiant : pour tout x, soit ν(P(x)) = V, soit ν(P(x)) = F.
1.2 Exemples
Consid´erons les ´enonc´es suivants :
•P= ’425 est un nombre pair’
•P0= ’3 divise 99’
•P00 = ’πest peut-ˆetre un nombre rationnel’
•Si nest un entier naturel, P(n)=’nest un multiple de 3’
Alors:
•Pest une proposition logique et a comme valeur de v´erit´e F.
•P0est une proposition logique et a comme valeur de v´erit´e V.
•Pn’est pas une proposition logique.
•P(n) est une proposition logique d´ependant du param`etre entier n. Par ex-
emple P(15) a la valeur V, et P(8) a la valeur F.
1Il existe d’autres types de logiques, non-classiques, comme la logique `a trois ´etats, ou bien
encore la logique floue (“fuzzy logic”); cette derni`ere a des applications tr`es concr`etes dans la vie
de tous les jours.
2

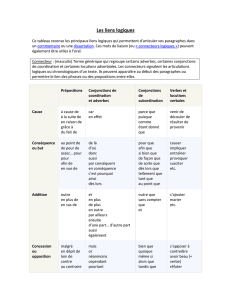
1.3 Connecteurs logiques
On dispose de cinq connecteurs fondamentaux :
non, et, ou, ⇔,⇒,
Soient Pet Qdeux propositions logiques,
•non(P) est la n´egation de la proposition P
•P et Q est une proposition logique vraie seulement si Pet Qsont simul-
tan´ement vraies.
•P ou Q est une proposition logique vraie quand au-moins une des deux est
vraie.
•P⇔Qse lit “P´equivaut `a Q” ou bien “Psi et seulement si Q” (´equivalence
logique); elle est vraie seulement quand les deux propositions Pet Qont des
valeurs de v´erit´e identiques.
•P⇒Qse lit “Pimplique Q” (implication logique). Il s’agit l`a de l’´etape
´el´ementaire dans tout raisonnement logique et, paradoxalement, c’est le con-
necteur qui est le moins ´evident `a d´efinir... (voir plus loin). Si P⇒Qest
vraie, on dira que Qest une condition n´ecessaire pour Pet que Pest une
condition suffisante pour Q.
Plus g´en´eralement, un connecteur logique C`a narguments (n´etant un entier na-
turel) est une correspondance :
(P1, . . . , Pn)7−→ C(P1, . . . , Pn)
associant `a tout n-uplet de propositions logiques (P1, . . . , Pn) une nouvelle proposi-
tion logique Q:= C(P1, . . . , Pn). Autrement dit, les connecteurs logiques permettent
de fabriquer de nouvelles propositions logiques `a partir de propositions existantes,
un peu comme un jeu de Lego.
Par exemple, non est un connecteur `a un argument; et,ou,⇒et ⇔sont des
connecteurs `a deux arguments.
Un connecteur se d´efinit par la donn´ee de sa table de v´erit´e : il s’agit d’un tableau
`a 2ncolonnes et n+1 lignes donnant la valeur de v´erit´e de C(P1, . . . , Pn) pour chaque
configuration possible (ν(P1), . . . , ν(Pn)) (il y a autant de configurations possibles
que d’applications {1, . . . , n}→{V, F }).
Donnons donc les tables de v´erit´e de nos trois premiers connecteurs fondamen-
taux :
PV F
non(P) F V
3

PV V F F
QV F V F
P et Q V F F F
PV V F F
QV F V F
P ou Q V V V F
L’implication et l’´equivalence logiques sont ensuite d´efinies comme sous-produits de
ces trois premiers connecteurs :
D´efinition 1.3.1
[P⇒Q] := non(P)ou Q. (1)
[P⇔Q] := [P⇒Q]et [Q⇒P].(2)
Le Lecteur aura soin de v´erifier que les deux d´efinitions (1) et (2) donnent nais-
sance aux deux tables de v´erit´e suivantes :
PV V F F
QV F V F
P⇒QV F V V
PV V F F
QV F V F
P⇔QV F F V
Un bon moyen mn´emotechnique pour m´emoriser ces tables consiste `a se rappeler
les relations suivantes :
ν(P etQ) = Vssi ν(P) = ν(Q) = V(3)
ν(P ouQ) = Fssi ν(P) = ν(Q) = F(4)
ν(P⇒Q) = Fssi ν(P) = Vet ν(Q) = F(5)
ν(P⇔Q) = Vssi ν(P) = ν(Q) (6)
Exercice 1.3.1 V´erifier que le ’et’, le ’ou’ et l’´equivalence logique sont des ’lois’
commutatives et associatives.
4

1.4 Faux implique vrai ?
Que ce soit par sa table de v´erit´e ou par sa d´efinition, l’implication logique pose
toujours quelques petits probl`emes de compr´ehension2. Voici un moyen de se con-
vaincre que “Faux implique vrai” n’est pas une vue de l’esprit : ´etant donn´ees deux
variables r´eelles xet y, notons P(x, y) la proposition x=yet Q(x, y) la proposition
x2=y2. Il est clair que la proposition P(x, y)⇒Q(x, y) est toujours vraie (ie:
quelles que soient les valeurs de nos deux variables); elle est donc en particulier
vraie si on prend (x, y) = (−3,3)...
1.5 Formes propositionnelles tautologiques
On appellera forme propositonnelle tautologique une proposition A(P1, . . . , Pn) qui
est toujours vraie quelles que soient les valeurs de v´erit´e des propositions com-
posantes P1, . . . , Pn; une forme propositionnelle tautologique peut-ˆetre consid´er´ee
comme un th´eor`eme du calcul propositionnel. On d´emontre (exercice !) que l’on a
les formes propositionnelles tautologiques suivantes :
1. P ou non(P) (principe du tiers-exclus).
2. non(P et non(P)) (principe de non-contradiction).
3. non(non(P)) ⇔P(involutivit´e).
4. non(P et Q)⇔non(P)ou non(Q) (Loi de De Morgan - I).
5. non(P ou Q)⇔non(P)et non(Q) (Loi de De Morgan - II).
6. (P⇒Q)⇔(non(Q)⇒non(P)) (contraposition).
7. (P⇒Q et P )⇒Q(principe du syllogisme).
8. (P⇒Q et non(Q)) ⇒non(P) (raisonnement par l’absurde).
9. (P⇒Q et Q ⇒R)⇒(P⇒R) (enchanement logique).
10. P et (Q ou R)⇔(P et Q)ou (P et R) (distributivit´e - I - et/ou).
11. P ou (Q et R)⇔(P ou Q)et (P ou R) (distributivit´e - II - ou/et).
2et ceci, bien que ce soit le raisonnement logique de base !
5