quadrilateres particuliers

QUADRILATERES PARTICULIERS
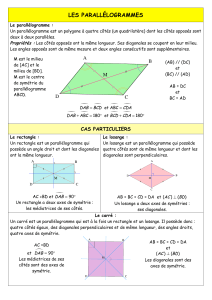
Parallélogramme
Définition :
Un parallélogramme est un quadrilatère dont les côtés opposés
sont parallèles.
Propriétés :
• Les côtés opposés d’un parallélogramme sont de même
longueur.
• Les diagonales d’un parallélogramme ABCD se coupent en
leur milieu. Dit autrement :
• I, le point d’intersection des diagonales, est le milieu de
[AC] et de [BD].
Figure
:
•
I, le point d’intersection des diagonales, est le centre de symétrie du parallélogramme.
• Les angles opposés d’un parallélogramme ont la même mesure.
• Deux angles consécutifs d’un parallélogramme sont supplémentaires : La somme de leur mesure est
180°.
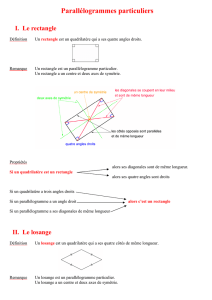
Rectangle
Définition :
Un rectangle est un quadrilatère ayant 4 angles droits.
Propriétés :
• Le rectangle est un parallélogramme particulier : il en possède
donc toutes les propriétés. De plus :
• Les diagonales d’un rectangle ont la même longueur.
• On peut tracer le cercle circonscrit de tout rectangle.
• Un rectangle a deux axes de symétrie : les médiatrices de ses
côtés.
Losange
Définition :
Un losange est un quadrilatère ayant ses 4 côtés de la même
longueur.
Propriétés :
• Un losange est un parallélogramme particulier : il en possède
donc toutes les propriétés. De plus :
• Les diagonales d’un losange sont perpendiculaires.
• Un losange a deux axes de symétrie : ses diagonales.
(BD) est la médiatrice de [AC].
(AC) est la médiatrice de [BD].
Carré
Définition :
Un carré est un quadrilatère ayant 4 angles droits et ses 4 côtés de
la même longueur.
Dit autrement : Un carré est à la fois un rectangle et un losange.
Propriétés :
• Le carré possède toutes les propriétés du parallélogramme, du
rectangle et du losange. En conséquence :
• Un carré possède 4 axes de symétrie.