Le parallélogramme (Chap7)

Parallélogrammes particuliers (18)
I. Les parallélogrammes particuliers
RECTANGLE
LOSANGE
CARRE

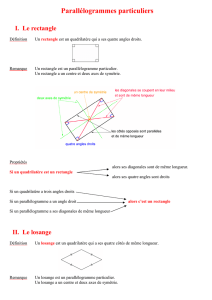
Propriétés
Si un quadrilatère est un rectangle, alors :
•il a quatre angles droits ;
• c’est un parallélogramme ;
•ses diagonales ont la même longueur ( et le même
milieu ) ;
•il a un centre de symétrie et deux axes de symétrie
(médiatrices des côtés).
II. Le rectangle

Comment reconnaître ou construire un rectangle ?
Si un parallélogramme a un angle droit, alors c’est
un rectangle.

Si un parallélogramme a ses diagonales
de même longueur, alors c’est un rectangle.

Propriétés
Si un quadrilatère est un losange, alors :
•il a 4 côtés de même longueur ;
• c’est un parallélogramme ;
•ses diagonales sont perpendiculaires ( et ont le même
milieu ) ;
•il a un centre de symétrie et deux axes de symétrie
(ses diagonales).
III. Le losange