2nde Jeudi 24 mars 2016 DST de MATHEMATIQUES 2h sans

2nde Jeudi 24 mars 2016
DST de MATHEMATIQUES
2h sans document. Calculatrice autorisée.
Le barème est approximatif.
Exercice 1 (4 points):
1) Déterminer, sans justifier, encadrer
x
1
lorsque
x
] ;
5
7
[.
2) Résoudre dans ℝ l’équation et l’inéquation suivantes :
a)
0
10020100
2
2
xx x
; b)
62 14 12484 x
x
xx
.
Exercice 2 (9 points):
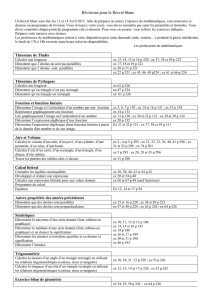
Le schéma suivant explique le fonctionnement de l’œil. Le segment [AB] représente un
objet. Ce dernier est vu par une personne car son image se projette au fond de l’œil sur la
rétine. Pour construire géométriquement l’image de [AB], on considère deux rayons
lumineux particuliers qui partent du point B : celui qui passe par le centre de la lentille O,
qui n’est pas dévié, et celui qui est parallèle à l’axe, qui passe par le point donné F, le
foyer de la lentille.
Les points A, O et F appartiennent à la droite (xx’) appelée axe focal.
La droite  (représentant le cristallin) est la droite perpendiculaire à (xx’) passant par O.
Le segment [AB] (représentant l’objet vu) est perpendiculaire à (xx’).
La droite parallèle à (xx’) passant par B coupe  en C ; la droite (CF) coupe (BO) en B’.
La droite perpendiculaire à (xx’) passant par B’ coupe (xx’) en A’.
La question 3) peut être traitée même si les questions 1) et 2) ne l’ont pas été.
1) Démontrer que :
OF
FA
OA
OA '' 
.

2) a) Dans cette construction, on admet que :
OFOAFA  ''
.
Montrer que :
'
111 OAOFOA 
.
b) Pour la suite, on note :
xOA 
, et on pose :
8OF
.
Montrer que :
8
8
' xx OA
.
3) Soit
f
la fonction définie par
8
8
)(  xx xf
, où
xOA 
.
a) Déterminer l’ensemble de définition de la fonction
f
, noté
f
D
.
b) Quelle est la nature de la fonction
f
? Justifier.
c) Montrer que pour tout x appartenant à
f
D
,
8
64
8)(   x xf
puis étudier le sens de variation de la fonction
f
sur l’intervalle ] 8 ; [ par
inégalités successives.
d) On admet que f est strictement décroissante sur l’intervalle [ 0 ; 8[. Dresser le tableau
de variations de la fonction
f
sur [ 0 ; 8[∪] 8 ; [.
e) Résoudre algébriquement dans ℝ l’inéquation
10)( xf
.
4) On donne l'algorithme suivant :
Variables: X, Y: nombres réels
Initialisation: X prend la valeur 35
Y prend la valeur f(X)
Traitement: Tant que Y > 10 faire
X prend la valeur X + 1
Y prend la valeur f(X)
Fin tant que
Sortie : Afficher X
a) Le faire fonctionner en complétant le tableau ci-dessous après l'avoir recopié
(rajouter si besoin des lignes)
X
Y
Condition Y>10
Avant le début de la boucle
Après le 1er passage dans la boucle
Après le 2ème passage dans la boucle
.................................................................
...............................................................

b) Que fait cet algorithme? Qu’affiche-t-il ? Est-ce cohérent avec les résultats des
questions précédentes?
Exercice 3 (4 points)
ABC est un triangle rectangle en A.
C1 est le cercle de centre B et de rayon BA ; C2 est le cercle de centre C et de rayon CA.
Une droite (D) passant par A coupe C1 en L et C2 en M. On note O le point d’intersection
des droites (LB) et (MC).
Le but de l’exercice est de démontrer que les droites (OL) et (OM) sont perpendiculaires.
1) Déterminer la nature des triangles LBA et ACM.
2) Que peut-on dire des angles 𝐿𝐴𝐵
̂ et 𝐶𝐴𝑀 ̂ ?
3) Déterminer la nature du triangle LOM puis conclure.
Exercice 4 (3 points)
Soit ABC un triangle. Les points K, L et M sont les milieux respectifs des segments [BC],
[ AC] et [ AB], et H est le pied de la hauteur issue de A.
Démontrer que le quadrilatère MHKL est un trapèze tel que MH = KL..