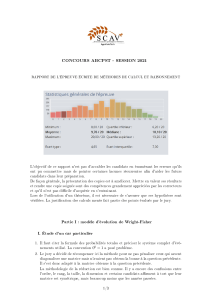
Regression linéaire non gausienne

n(xi, yi), i = 1 . . . n
yi=β0+β1xi,1+·+βpxi,p +i, i = 1, . . . n,
= (1, . . . , n)T
1, . . . , n
E1= 0
E2
1=σ2
ˆ
β β
PXX hn
PX
hn→0n→+∞ˆ β
1
nαXTX→Q Q α > 0
hn→0⇒nα/2(ˆ β−β)L −−−−→
n→∞ N(0, σ2Q−1).
H0:KTβ= 0 H1:KTβ6= 0” KT
k×(p+ 1) Rg(K)≤p+ 1
hn→0 =⇒ˆ F=(KTˆ
β)T[KT(XTX)−1K]−1KTˆ β
Rg(K)s2
L
−−−−→
n→∞
1
Rg(K)χ2(Rg(K)).
ˆ
F∼ F[k, n −p]
ˆ
FL −−−−→
n→∞
1
kχ2(k).
n

p= 3 xi= (xi,1, xi,2, xi,3)T
[a, b]
a, b xi
 1, . . . , n
λ= 1
[−A, A]
n
α= 1 xi
[a, b]
ˆ
β s2F=MCR
MCres
m= 100
λ A > 0