Feuille d`exercices No 3 Bis - Récursivité

F0= 0 F1= 1 Fn=Fn−1+Fn−2
n≥2n
FnF20
.
Fn
x
xnn
xn=(xn
2.xn 2, si n
xn−1
2.xn−1 2.x si n .
xn
xn
a b
d d a b u a b u d
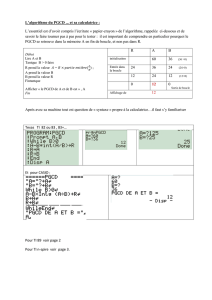
a b P GCD 60 45 15
P GCD a 0
b r a b
P GCD(a, b) = P GCD(b, r)|r|<|b|
P GCD a b
d P GCD
a b (u, v)
d=u×a+v×b, .
[u, v]
3 = P GCD(9,15) [u, v] 3 =
u×9 + v×15

b
a=q×b+r
d=u×a+v×b=u×(q×b+r) + v×b= (u×q+v)×b+u×r.