Correction de cet exercice.

Correction des exercices de physique d’AP.
Exercice 1 : accélération du motard.
Rappels : sur l’annexe 1cm représente 3m dans la réalité. L’échelle pour les vitesses sera 1cm représente 4m.s-1.
1) Pour représenter ces vecteurs, il faut d’abord calculer leurs normes puis en déduire grâce à l’échelle leur
longueur. Pour ⃗⃗⃗⃗
𝑣2 , on mesure G1G3, on trouve 4,5cm ce qui fait en réalité 13,5m d’où on a v 2=
4,5×3
=8,4m.s-1.
2×0.8
Avec l’échelle 1cm pour 4m.s-1, on doit tracer un vecteur de 2,1cm. Voir construction ci-dessous.
8,9×3
Pour ⃗⃗⃗
𝑣4 , on mesure G3G5, on trouve 8,9cm d’où on a v4= 2×0.8=16,7m.s-1. Avec l’échelle 1cm pour 4m.s-1, on doit
tracer un vecteur de 4,2cm. Voir construction ci-dessous.
2) On a ⃗⃗⃗⃗
𝑎3 =
⃗⃗⃗⃗3
∆𝑣
2∆𝑡
=
⃗⃗⃗⃗
⃗⃗⃗⃗2
𝑣4 −𝑣
.
2∆𝑡
3) Première méthode : on construit le vecteur ∆𝑣
⃗⃗⃗⃗3 en translatant le vecteur ⃗⃗⃗
𝑣4 au point 3 puis le vecteur –𝑣
⃗⃗⃗⃗2 à
l’extrémité du vecteur ⃗⃗⃗
𝑣4 . On trace alors ∆𝑣
⃗⃗⃗⃗3 , on mesure sa longueur et on déduit sa valeur. Voir construction ci8,4
dessous. On trouve 2,1cm soit Δv3=8,4m.s-1. Il ne reste plus qu’à calculer a3=1,6 = 5,3𝑚. 𝑠 −2 .
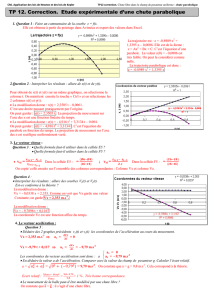
Deuxième méthode : On sait que l’accélération est la dérivée de la vitesse. Nous avons la courbe représentant
la vitesse en fonction du temps. La dérivée correspond au coefficient directeur de cette droite soit 5m.s-2.
4) On cherche grâce au premier graphique la durée nécessaire pour atteindre 90km/h soit 25m.s-1. On trouve 5s.
On regarde sur la courbe 2 la distance parcourue au bout de 5s soit 60m.
Exercice 2 :
L’équation horaire du mouvement d’un point sur un axe ox est x(t)=6t+2 où x s’exprime en m et t en
secondes.
1) Déterminer, en les justifiant, les unités des coefficients 6 et 2 dans l’équation horaire.
Chaque terme de l’équation s’exprime en m donc [6t]=m or [t]=s donc [6]=m.s -1 de plus, on doit avoir
[2]=m.
2) Donner la définition de la vitesse vx du point en fonction de x et retrouver sa valeur numérique.
On a 𝑣𝑥 =
𝑑𝑥
𝑑𝑡
donc vx=6m.s-1.
3) En déduire la nature de son mouvement.
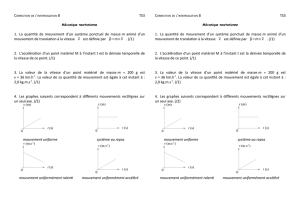
Le mouvement est rectiligne (mouvement sur un axe) et uniforme.