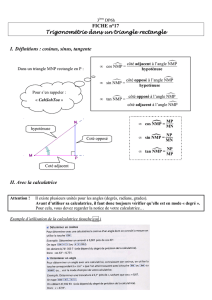
diviser et conquérir - Université de Genève

Algorithmique
Diviser et conquérir
Mauvaise nouvelle : il n’existe pas d’algorithme pour trouver un algorithme
Diviser un problème en sous-problèmes
Mais, il existe des techniques de conception des algorithmes :
Résoudre séparément les sous-problèmes
Combiner les solutions partielles
• diviser et conquérir
• la programmation dynamique
• les algorithmes récursifs et le retour arrière (backtracking)
• les algorithmes gloutons
G. Falquet, CUI, Université de Genève
1 de 22
Exemple – MINIMAX
G. Falquet, CUI, Université de Genève
2 de 22
Approche “diviser et conquérir”
• diviser S en deux ensembles S1 et S2 de même taille,
Trouver le plus petit et le plus grand élément d’un ensemble S de taille n = 2k .
• chercher le min et le max dans S1 et S2,
• combiner les résultats en prenant le min des min et le max des max.
Algorithme itératif :
MAX ← un élément quelconque y de S
MIN ← y
pour chaque élément x de S – {y} {
si (x > MAX) MAX ← x
si (x < MIN) MIN ← x
}
procédure MAXMIN(ensemble(T) S) retourne (T, T)
si (card(S)) = 2 et S = {x1, x2}
si (x1 < x2) retourne (x1, x2) sinon retourne (x2, x1)
sinon {
diviser S en S1 et S2 de même taille
(a1, b1) ← MAXMIN(S1)
(a2, b2) ← MAXMIN(S2)
retourne (min(a1, a2), max(b1, b2))
}
Complexité en temps :
2(n-1) comparaisons.
G. Falquet, CUI, Université de Genève
3 de 22
G. Falquet, CUI, Université de Genève
4 de 22
Complexité
Exemple-2 : SOUS-SUITES MAXIMALES
Nombre de comparaison en fonction de la taille n de S
T(n)
= 1
= 2T(n/2) + 2
Etant donné une suite de nombres positifs, nuls ou négatifs
S = <s1 , s2 , …, sn >
si n = 2
si n > 2
trouver i et j (i≤j) tels que si + s i+1 +s i+2 + … + sj soit la plus grande possible.
S = <1, -2, 5, -3, -1, 2, -1, 9, -8, 7, 1>
Cette équation a pour solution la fonction
T: n → 3n/2 - 2
sous-suite max :
Algorithme exhaustif
Algorithme est 25% meilleur que le précédent.
essayer toutes les valeurs possibles de i et j,
donc n + (n-1) + (n-2) + … + 2 + 1 = (n (n+1))/2 sommes à calculer.
Chaque somme peut se calculer en une opération à partir de la somme précédente.
Donc effectuer (n (n+1))/2 additions et comparaisons.
G. Falquet, CUI, Université de Genève
5 de 22
G. Falquet, CUI, Université de Genève
Diviser
Algorithme
On divise S en deux parties S1 = <s1 , …, sn/2> et S2 = <s n/2+1, …, s n>
procedure MAXSOM(a, b)
si (a = b) retourne s[a]
sinon {
d = (a+b)/2; max1 ← MAXSOM(a, d); max2 ← MAXSOM(d+1, b)
// la plus grande somme qui commence en S1 et finit à d
m1 ← s[d]; somme ← s[d];
pour i de d-1 à a {
somme ← somme + s[i]
si (somme > m1) m1 ← somme}
//. la plus grande somme qui commence en d+1 et finit dans S2
m2 ← s[d+1]; somme ← s[d+1];
pour i de d+1 à b {
somme ← somme + s[i]
si (somme > m2) m2 ← somme }
retourner max(max1, max2, m1+m2)
Trois cas possibles
• la sous-suite max. se trouve entièrement dans S1;
• elle se trouve entièrement dans S2;
• elle commence dans S1 et finit dans S2.
Dans ce dernier cas les éléments sn/2 et sn/2+1 appartiennent à la sous-suite.
< s1 ……………………………sn >
G. Falquet, CUI, Université de Genève
6 de 22
7 de 22
G. Falquet, CUI, Université de Genève
8 de 22
Complexité
Equilibrage des partitions
Le nombre de sommes et comparaisons est
T(n)
=1
= 2T(n/2) + 2n
Tri de n nombres par recherche du plus petit
• trouver le plus petit élément du tableau
si n = 1
si n>1
• échanger le 1er avec le plus petit
• trier les n-1 éléments restants
Calcul
k
Complexité O(n2 )
k-1
T(2 ) = 2T(2
k+1
)+2
= 2(2T(2k-2 )+2k)+2k+1 = 22T(2 k-2) + 2 k+1 + 2k+1
= 2 2T(2T(2k-3 )+2k-1) + 2k+1 + 2k+1 = 23 T(2k-3 )+2k+1 + 2k+1 + 2 k+1
1
=…
n–1
= 2 kT(1) + k(2k+1) = 2 k + 2k2 k = n + 2log(n) n ∈ O(n log n)
G. Falquet, CUI, Université de Genève
9 de 22
G. Falquet, CUI, Université de Genève
Technique équilibrée : tri-fusion
10 de 22
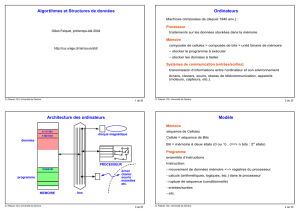
Programmation dynamique
Le tri-fusion est une méthode par division équilibrée
• trier les éléments de 0 à n/2-1
• trier les éléments de n/2 à n
• fusionner les deux parties triées dans un nouveau tableau
Dans certains cas les algorithmes récursifs descendants sont inneficaces car ils
recalculent plusieurs fois la même chose.
Exemple. Etant donné une monnaie qui possède des pièces de valeur v1 , v2 , …, vk et
une somme s, quel est le nombre minimum de pièces pour obtenir cette somme ?
Un algorithme récursif descendant peut s’écrire comme
NMP(s) =
si s = 0 retourne 0
sinon retourne 1 + min{ NMP(s – vi) | 1 ≤ i ≤ k et s – vi ≥ 0 }
Temps d’exécution:
T(n)
=0
si n = 1
= 2T(n/2) + n si n>1
Complexité: O(n log n)
G. Falquet, CUI, Université de Genève
11 de 22
G. Falquet, CUI, Université de Genève
12 de 22
Exemple
Programmation dynamique
s = 15 et v1 = 1, v 2 = 2, v 3 = 7, v 4 = 10
Idée : stocker les résultats partiels déjà obtenus.
NMP(15)
v1 --> NMP(14)
v1 --> NMP(13) …
v2 --> NMP(12) …
v3 --> NMP(7) …
v4 --> NMP(4) …
v2 --> NMP(13) -- déjà calculé une fois
v1 --> NMP(12) … déjà calculé une fois
v2 --> NMP(11) …
…
v3 --> NMP(8)
v1 --> NMP(7) -- déjà calculé…
v2 --> NMP(6)
Calcul “bottom-up”, on commence par calculer les résultats pour les cas les plus
simples :
NMP(0) = 0 -- cas trivial
NMP(1) = 1 + NMP(0) = 1
NMP(2) = 1 + min{NMP(1), NMP(0)} = 1
NMP(3) = 1 + min{NMP(2), NMP(1)} = 2
NMP(4) = 1 + min{NMP(3), NMP(2)} = 2
NMP(5) = 1 + min{NMP(4), NMP(3)} = 3
NMP(6) = 1 + min{NMP(5), NMP(4)} = 3
NMP(7) = 1 + min{NMP(6), NMP(5), NMP(0)} = 1
NMP(8) = 1 + min{NMP(7), NMP(6), NMP(1)} = 2
NMP(9) = 1 + min{NMP(8), NMP(7), NMP(2)} = 2
Complexité en temps : O(sk)
Complexité exponentielle (k s/c)
G. Falquet, CUI, Université de Genève
13 de 22
Retour arrière (backtracking)
G. Falquet, CUI, Université de Genève
14 de 22
Exemple. Le problème des huit reines
Explorer "intelligemment un espace de solutions potentielles".
Un échiquier de n × n cases
=> s’arrêter dès qu’il n’y a plus d’espoir
on veut disposer n reines sans qu’elles se menacent mutuellement.
conditions à satisfaire:
• deux reines ne peuvent se trouver sur la même ligne
• deux reines ne peuvent se trouver sur la même colonne
• deux reines ne peuvent se trouver sur la même diagonale
X
X
Solutions partielles : 1 reine placée, 2 reines, 3 , …
X
OK
G. Falquet, CUI, Université de Genève
15 de 22
G. Falquet, CUI, Université de Genève
16 de 22
Exemple
Programmation
sur un échiquier 4 × 4:
classe Solution
// variable mémorisant la solution (partielle) actuelle
Description_solution s
méthode essayer()
si (s est une solution complète) { afficher s }
sinon {
pour toute solution partielle s’ constructible à partir de s {
si (s’ peut éventuellement mener à
une solution correcte) {
memoS ← s; s ← s’; essayer();
s ← memoS
}
}
}
X
X
G. Falquet, CUI, Université de Genève
17 de 22
classe SolutionNReines
18 de 22
placer_reine(i, j)
colonne[j] ← i; rangée[i] ← vrai;
diagonale1[i+j] ← vrai; diagonale2[N+i–j] ← vrai
}
case_non_menacée(i, j)
retourne non rangee[i] et non diagonale1[i+j]
et non diagonale2[N+i–j]
[]
// mémorisation de la solution
int colonne[N] // ligne de chaque reine dans chaque colonne
// uniquement pour accélérer les tests
booléen rangee[N], diagonale1[2*N–1] , diagonale2[2*N–1]
essayer_colonne(j)
i←N
tant que (i > 0) {
si (case_non_menacée(i, j)) {
placer_reine(i, j)
si (j>1) essayer_colonne(j–1)
sinon afficher_échiquier
enlever_reine(i, j)
}
}
G. Falquet, CUI, Université de Genève
G. Falquet, CUI, Université de Genève
19 de 22
G. Falquet, CUI, Université de Genève
20 de 22
Algorithmes gloutons
Gloutons (conception)
Un algorithme glouton construit une solution à un problème en faisant à chaque étape
le choix le plus “facile”.
Les algorithmes gloutons sont en général faciles à inventer, car ils correspondent à
l’intuition.
Exemple 1. Min. de pièces de monnaie
Mais l’intuition peut se révéler fausse, il faut donc démontrer formellement que
l’algorithme est correct.
S : la somme à atteindre
A ←0
NP ← 0
tant que (A < S) {
choisir la pièce v i de plus grand valeur telle que A+vi ≤ S
A ← A + vi; NP ← NP + 1
}
p.ex. l’algorithme de Kruskal est un algorithme glouton.
Il n’est pas simple de montrer qu’il est correct.
Si l’on ne recherche pas la meilleure solution mais une solution “acceptable” on peut
employer un algorithme glouton non optimal.
Un algorithme glouton peut également ser vir à produire une première solution, non
optimale, que l’on peut ensuite améliorer par des techniques telles que TABOU ou le
“recuit simulé”.
OK dans le cas où v1 = 1, v2 = 2, v3 = 5 et v4 = 10.
Ne marche pas si v1 = 1, v 2 = 4, v 3 = 6 et S = 8..
G. Falquet, CUI, Université de Genève
21 de 22
G. Falquet, CUI, Université de Genève
22 de 22