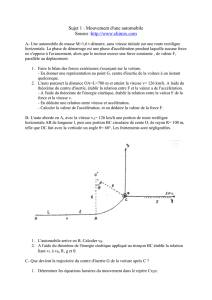
TD: Cinématique du point matériel xy OCM θ R r

TD: Cinématique du point matériel
Exercice 1 : mouvement d’un point matériel sur un cercle
Dans le référentiel terrestre R, un point M décrit une trajectoire circulaire de centre C et de
rayon R dans le plan de la figure (Oxy). Il est repéré en coordonnées polaires comme l’indique la
figure ci-dessous et se déplace avec une vitesse angulaire
1. Déterminer l’équation en polaire de la trajectoire de M en coordonnées polaires.
2. Exprimer, dans la base (er, eθ,ez) , les vecteurs vitesse et accélération de ce point par
rapport au référentiel R. Quelles sont leurs normes respectives ?
3. Montrer que le vecteur accélération de ce point peut s’exprimer simplement en fonction de
ω0 et du vecteur CM ? En déduire que le mouvement de M est circulaire uniforme et qu’il
s’effectue avec une vitesse angulaire que vous préciserez.
Exercice 2 : Trois chiens se poursuivent
A l’instant t=0, trois chiens A, B, C sont situés aux trois sommets d’un triangle équilatérale de
côté a et se mettent en mouvement. Le module de leur vitesse, identique pour les trois, est v
. Le chien A se dirige constamment vers B, qui se dirige constamment vers C, qui, lui-même, se
dirige constamment vers C, qui, lui-même, se dirige constamment vers A.
1. Quelle figure forment les trois chiens à chaque instant t ?
2. Déterminer la trajectoire suivie par chaque chien ainsi que les lois horaires définissant le
mouvement sur ces trajectoires. On utilisera les coordonnées polaires. Déterminer r(t)
et θ(t) et r=f(θ).
3. A quel instant les trois chiens se rencontrent-ils ? Quelle distance auront-ils parcouru ?
Exercice 3: Mouvement circulaire
Un point M se déplace sur un cercle de rayon R. A t=0 M est en O. Son accélération radiale est à
tout instant égale à -3t. Déterminer à l'instant t la position, la vitesse et l'accélération.
Exercice 4: Accélération dépendant de la position
Une particule, initialement au repos en x0, se déplace rectilignement avec une accélération
. Calculer la vitesse de la particule au point d’abscisse x.
x
y
O
C
M
θ
er
eθ
R
+
r

Exercice 5: Etude d'un mouvement sur une cycloïde
Une roue de rayon R roule sans glisser sur un rail rectiligne Ox. Un point M à la périphérie de la
roue coïncide à la date t=0 avec l’origine O du repère, le centre C de la roue a une vitesse V0
positive, constante, parallèle à Ox, dans le plan xOz. Roulement sans glissement : Le point de
contact I de la roue avec le rail a une vitesse nulle.
1. Déterminer les coordonnées x et z du point M : on introduira l’angle θ(t), angle dont la
roue a tourné depuis la date t=0. Déterminer la vitesse du point M (dθ/dt=ω vitesse
angulaire). Exprimer la condition de roulement sans glissement et en déduire θ(t) en
fonction du temps t. Déterminer l’accélération du point M.
2. Représenter la trajectoire z=f(x) en notant sur ce schéma quelques points
caractéristiques (points de vitesse nulle et points de vitesse maximale).
3. Déterminer la longueur L d’un arc de cycloïde.
Exercice 6: Mouvement d’un point matériel sur une conique. Hodographe
Dans le plan orthonormé (OXY) de vecteurs unitaires , on considère une particule M telle que
les composantes de son vecteur vitesse suivant OY et suivant la perpendiculaire à OM sont valent
respectivement a et b; avec a et b des constantes au cours du mouvement. On utilisera les
coordonnées polaires
1. Déterminer la trajectoire de M dans le cas général où a≠0 et b≠0.
Etudier les 3 cas particuliers: a=0, b=0 et a=b≠0.
2. Déterminer l’hodographe du mouvement.
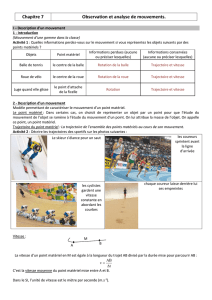
Exercice 7: Un promeneur et son chien
Un promeneur A suit son chemin rectiligne avec une vitesse constante V0. A l'instant initial, son
chien M se trouve à une distance d sur la même perpendiculaire au chemin. Puis il court vers son
maitre à la vitesse v (v=cte). On cherche à déterminer la durée de la poursuite. Soit x et y les
coordonnées de M, r=AM et θ défini sur le schéma.
1. Exprimer dx/dt et dy/dt en fonction de v et de θ, puis x et y en fonction de v0, r, θ et t. En
déduire deux équations différentielles en r(t) et θ(t).
x
z
O
θ
C
M

2. En déduire une équation différentielle en r(θ). Vérifier que est la
solution qui tient compte des conditions initiales.
3. Quelle condition v et v0 doivent-elles vérifier pour que le problème ait une solution? Quelle
est la valeur finale de θ? Ecrire l'équation différentielle de θ(t).
4. Sachant que , déterminer la durée t de la poursuite en
fonction de d, v et v0.
Eléments de réponse :
Ex.1 :
Ex.2 :Les trois chiens forment un triangle équilatéral à chaque instant t.
Ex.3 :
Ex.4 :
Ex.5 :
Ex.6 :
Ex.7 :