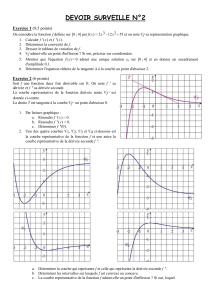
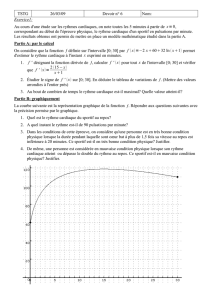
dh - WebCampus

Quelques notions de base
1. Mesure des angles
On peut mesurer les angles en degrés, en grades, en tours ou en radians, la conversion se
faisant selon le barème suivant :
360 degrés = 400 grades = 1 tour = 2π radians.
Le radian vient naturellement lorsqu'on considère que la longueur d'un arc de cercle est
proportionnelle à l'angle au centre qui le sous-tend : si l'angle au centre a une mesure ϑ , selon
l'unité choisie, on trouvera pour la longueur de l'arc sous-tendu (le rayon étant de longueur
R) :
L = 2π R
L = 2π R
ϑ
360
ϑ
400
L = 2π Rϑ
L = Rϑ
La dernière expression étant manifestement la plus condensée / la plus simple. De cette
définition, il résulte qu'un angle au centre d'un radian sous-tend un arc de longueur R, soit un
peu moins du sixième de la circonférence ; il correspond donc à un peu moins de 60°, plus
exactement 57° 17' 44".
Voici la table de conversion pour quelques angles courants :
30°
60°
120°
150°
210°
240°
300°
330°
π/6
π/3
2π / 3
5π / 6
7π / 6
4π / 3
5π / 3
11π / 6
π/4
π/2
3π / 4
π
5π / 4
3π / 2
7π / 4
2π
45°
90°
135°
180°
225°
270°
315°
360°
La plupart des calculatrices, y compris celle figurant dans les programmes accessoires de
Windows, permettent de choisir l'unité employée pour exprimer les angles. Le tableur Excel
fonctionne aussi en radians.
Si on exprime les fonctions trigonométriques par un développement en série du type :
sin ϑ = ϑ −
cos ϑ = 1 −
ϑ3
3!
ϑ
2
2!
+
+
ϑ5
5!
ϑ
4
4!
−
−
ϑ7
7!
ϑ
6
6!
∞
+ … = ∑ ( −1)
n
n=0
∞
+ … = ∑ ( −1)
n =0
n
ϑ 2 n +1
( 2n + 1)!
ϑ 2n
( 2n ) !
l'expression ainsi écrite ne vaut que si l'angle est exprimé en radians.
Finalement, on peut encore relever que, tout comme les expressions x2 et x3 qui désignent au
départ respectivement l'aire d'un carré de côté x et le volume d'un cube d'arête x peuvent être
calculées hors de ce contexte, rien ne s'oppose à calculer le sinus ou le cosinus d'un nombre
quelconque. Ces fonctions sont omniprésentes dans la description de phénomènes oscillatoires
ou ondulatoires.
2. Dérivées
On ne donnera ici que des indications pratiques, sans démonstration.
2.1. Qu'est-ce que c'est ?
La dérivée d'une fonction f(x) est donnée par :
f ( x + δ x) − f ( x)
df
δf
= lim
=
lim
dx δ x→0
δx
déf δ x →0 δ x
df
d
ou
f , le choix s'effectuant le plus souvent sur des
dx
dx
critères de clarté typographique.
On peut écrire indifféremment
Par exemple, si f(x) = x3 :
f ( x ) = x3
f ( x + δ x) = ( x + δ x)
3

2
2
3
 ⇒ δ f = 3 x δ x + 3 xδ x + δ x
3
2
2
3
= x + 3 x δ x + 3 xδ x + δ x 
δf
= 3 x 2 + 3 xδ x + δ x 2
δx
δf
= 3x 2
lim
δ
x
δ x →0
Il résulte de cette définition que la dérivée d'une fonction constante est nulle.
2.2. Quelques dérivées typiques
d m
x = mx m −1
dx
d
sin x = cos x
dx
d
cos x = − sin x
dx
d x
e = ex
dx
d
1
ln x =
dx
x
L'expression donnée pour les dérivées de fonctions trigonométriques ne vaut que lorsque leur
argument est exprimé en radians.
Lorsqu'une fonction résulte de la somme de plusieurs fonctions, sa dérivée est la somme des
dérivées de chaque terme :
F ( x ) = f1 ( x ) + f 2 ( x ) ⇒
dF ( x )
dx
=
df1 ( x )
dx
+
df 2 ( x )
dx
Pour les produits et les quotients, c'est un peu plus compliqué. On a :
F ( x ) = f1 ( x ) f 2 ( x ) ⇒
et :
dF ( x )
dx
=
df1 ( x )
dx
f 2 ( x ) + f1 ( x )
df 2 ( x )
dx
f1 ( x )
F ( x) =
⇒
f2 ( x )
df1 ( x )
df 2 ( x )
f
x
−
f
x
(
)
(
)
2
1
dF ( x )
dx
= dx
2
dx
 f 2 ( x ) 
On peut considérer un exemple pour lequel la vérification est aisée. Si on prend :
f1 ( x ) = x 2 
⇒ F ( x ) = f1 ( x ) f 2 ( x ) = x 7
5
f 2 ( x ) = x 
on peut calculer directement :
dF ( x )
dx
dx 7
=
= 7 x6
dx
on peut aussi calculer :
df1 ( x )

dx 2
=
= 2x 

dx
dx
 ⇒
5
df 2 ( x ) dx
4
=
= 5x

dx
dx
dF ( x )
dx
=
df1 ( x )
df ( x )
f 2 ( x ) + f1 ( x ) 2
= 2 x6 + 5x6 = 7 x6
dx
dx
5
2
2x
x
x
5 x4
et vérifier la cohérence des deux modes de calcul.
On vérifie à partir de ce qui précède que si C est une constante et F(x) = C f(x), alors
dF ( x )
dx
=
df ( x )
df ( x )
dC
f ( x) + C
=C
dx
dx
dx
0
Un dernier cas est à considérer, celui où une fonction résulte de l'application successive de
deux fonctions :
F ( x ) = f  g ( x )  ⇒
dF ( x )
dx
=
df ( u )
du
dg ( x )
u= g ( x)
dx
Exemple :
F ( x ) = e− x
2
qui correspond à :
f ( x ) = ex
g ( x ) = − x2
L'application de la recette donnée ci-dessus conduit à :
df ( u )
du
dg ( x )
dx
=
u = g( x)
=
(
deu
du
d − x2
dx
= eu
u=g( x)
) = −2 x
u = g( x)
2 
= e− x 

 ⇒



dF ( x )
dx
= e − x ( −2 x ) = −2 xe − x
2
2
On peut éventuellement dériver à nouveau la dérivée d'une fonction, et répéter l'opération
(pourvu que ce soit possible, toutes les fonctions ne sont pas dérivables). On notera dans ce
cas :
n
d  d  d  d
 d
  ⋯ ( f ( x ) )    = n f ( x )
dx  dx  dx  dx
   dx
n fois
et on parlera de la dérivée énième de f ou encore de sa dérivée d'ordre n.
2.3. À quoi cela sert-il ?
Relevons que pour une fonction croissante, les variations δx et δf sont toujours de même signe
et ont donc un quotient positif, alors que pour une fonction décroissante, ces variations sont
toujours de signes opposés et ont donc un quotient négatif. Le signe du quotient est conservé
lors du passage à la limite. On déduit de ceci que le signe de la dérivée d'une fonction indique
si elle est croissante ou décroissante.
Par exemple, la dérivée de x2 vaut 2x et est positive lorsque x est positif, négative lorsque x est
négatif, ce qui correspond bien au fait que x2 croît pour les valeurs positives de x et décroit
pour les valeurs négatives.
L'annulation de la dérivée correspond à un point stationnaire, qui peut être :
•
•
•
un minimum, c'est le cas de la fonction x2 ;
un maximum, c'est le cas de la fonction –x2 ;
un point d'inflexion horizontale, c'est le cas de la fonction x3.
Lorsqu'on identifie un zéro de la dérivée d'une fonction, il faut donc encore en départager les
trois interprétations possibles.
Dans une première approche, on peut considérer les valeurs que prend la dérivée au voisinage
de son point d'annulation. Pour les exemples ci-dessus on voit que :
•
•
•
la dérivée de x2 vaut 2x et est négative pour x < 0 et positive pour x > 0 ;
la dérivée de –x2 vaut –2x et est positive pour x < 0 et négative pour x > 0 ;
la dérivée de x3 vaut x2 et est positive tant pour x < 0 que pour x > 0.
On en déduit que :
•
•
•
la succession – 0 + indique un minimum ;
la succession + 0 – indique un maximum ;
la succession + 0 + (ou – 0 –) indique un point d'inflexion horizontale d'une fonction
croissante (décroissante).
Une autre approche consiste à calculer la valeur de la dérivée seconde au point considéré.
Pour nos trois exemples, la dérivée seconde vaut, pour x = 0,
•
•
•
2 et est donc positive ;
–2 et est donc négative ;
2x et est donc nulle pour x = 0.
On déduit donc qu'un point stationnaire (une valeur de la variable pour laquelle la dérivée
première s'annule) est un minimum lorsque la valeur de la dérivée seconde, calculée en ce
point est positive, un maximum si elle est négative et un point d'inflexion horizontale si elle
est nulle. Cette première conclusion mène cependant à un résultat erroné si on considère la
fonction x4, qui a un minimum en 0 et dont les deux premières dérivées s'annulent en ce point.
La règle est que la nature d'un point stationnaire dépend de l'ordre de la première dérivée non
nulle en ce point. Si la première dérivée non nulle est d'ordre
•
•
•
•
pair et si sa valeur est positive, on est en présence d'un minimum ;
pair et si sa valeur est négative, on est en présence d'un maximum ;
impair et si sa valeur est positive, on est en présence d'un point d'inflexion horizontale
d'une fonction croissante ;
impair et si sa valeur est négative, on est en présence d'un point d'inflexion horizontale
d'une fonction décroissante.
On peut, à titre d'exercice, vérifier l'exactitude de la méthode pour des fonctions de type xm.
Attention, cette méthode ne permet pas de trouver les extrema si ceux-ci se situent à la
frontière de l'ensemble de définition de la fonction. Ainsi la fonction f(x) = x, définie sur
l'intervalle [0,1] atteint son maximum pour x = 1 et son minimum pour x = 0, sans qu'aucun de
ces points ne soit un point d'annulation de sa dérivée.
3. Fonctions de plusieurs variables
Si une fonction dépend de plusieurs variables, x1, x2… xi… xn, on appelle dérivée partielle par
rapport à la variable xi la fonction obtenue comme suit :
f ( x1 ,… , xi + δ xi ,… , xn ) − f ( x1 ,… , xi ,… , xn )
∂f
= lim
δ xi
∂xi δ xi →0
La notation à l'aide d'un d rond (∂) permet d'attirer l'attention sur le fait que la fonction dépend
d'autres variables en sus de celle par rapport à laquelle on dérive.
3.1. Points stationaires
Les points stationnaires d'une fonction de plusieurs variables sont ceux où toutes les dérivées
partielles s'annulent.
Pour être complet, signalons encore sans entrer dans les détails que la nature du point
stationnaire est en général déterminée par l'étude de la matrice des dérivées secondes (matrice
hessienne), c'est-à-dire du tableau carré dont les éléments sont donnés par :
hi , j =
∂2 f
∂xi ∂x j
3.2. Différentielle
Pour exprimer que fi(x1,…,xn) (i = 1,…,n) est la dérivée par rapport à xi d'une fonction
F(x1,…,xn) on note :
n
dF = f1 ( x ) dx1 + … + fi ( x ) dxi + … + f n ( x ) dxn = ∑ fi ( x ) dxi
i =1
où x représente (x1,…,xn).
Donc, si on rencontre dans le cours de thermodynamique une expression telle que
dU = ncɶv dT − pdv
cela signifie
U = U (T , v )
∂U
= ncɶv
∂T
∂U
= −p
∂v
4. Accroissements finis
Qu'il s'agisse d'une fonction d'une (n = 1) ou de plusieurs (n > 1) variables, on peut toujours
écrire de façon approchée, pour des accroissements petits, mais pas infinitésimaux
n
δ F ≈ f1 ( x ) δ x1 + … + f i ( x ) δ xi + … + f n ( x ) δ xn = ∑ fi ( x ) δ xi
i =1
5. Primitives et intégrales
Comme pour ce qui concerne les dérivées, on envisagera les choses d'un point de vue
pratique, sans chercher à atteindre la généralité ou la rigueur réservée à un cours d'analyse.
5.1. Primitives
Le pendant du problème consistant à trouver la (les) dérivée(s) d'une fonction est de trouver
une fonction inconnue dont on connaît la (les) dérivée(s). Nous ne considérerons ce problème
que dans le cas des fonctions d'une variable. La fonction F(x) dont la dérivée est une fonction
donnée f(x) est appelée sa primitive (on dit aussi : intégrale indéfinie). On note :
F ( x ) = ∫ f ( x ) dx
Cette fonction n'est définie qu'à une constante additive près, car on a toujours
d
d
 F ( x ) + C 
F ( x) =
dx
dx 
5.2. Intégrale
L'intégrale (on dit aussi : intégrale définie) d'une fonction f(x), prise sur un intervalle [a,b]
représente l'aire comprise entre le tracé de cette fonction et l'axe horizontal, comptée
positivement là où la fonction est positive et négativement là où elle est négative. Elle est
égale à la variation de la primitive de f entre les points a et b, ce que l'on notera :
b
∫
f ( x ) dx = F ( x ) ä = F ( b ) − F ( a )
b
a
La valeur de cette expression est indépendante de la constante arbitraire figurant dans la
définition de la primitive puisque
F ( b ) − F ( a ) =  F ( b ) + C  −  F ( a ) + C 
5.3. Quelques primitives typiques
x m+1
∫ x dx = m + 1 m ≠ −1
1
∫ x dx = ln x
m
∫ sin x dx = − cos x
∫ cos x dx = sin x
∫ e dx = e
∫ ln x dx = x ln x − x
x
x
Toutes ces relations sont vraies à une constante additive près.
5.4. Dérivée et intégrale
La relation entre dérivée d'une part et primitive ou intégrale d'autre part s'exprime par :
x
d
f ( x′ ) dx′ = f ( x )
dx ∫a
x
d
∫ dx′ f ( x′) dx′ = f ( x ) − f ( a )
a
où on prend soin d'utiliser des symboles différents pour la variable d'intégration (ci-dessus :
x') et pour les bornes de l'intervalle d'intégration (ci-dessus : a et x).
5.5. Exemple
Pour un corps lâché1 en chute libre au voisinage de la surface terrestre, l'équation de
mouvement s'écrit (on néglige la résistance de l'air) :
d
( mV ) = −mg
dt
où m est la masse du corps, V sa vitesse et g l'accélération (constante) de la pesanteur, les
positions étant rapportées à un axe vertical orienté positivement vers le haut dont l'origine est
prise au point de départ de la chute ; on compte le temps à partir de l'instant initial de la chute.
La masse étant constante on commence par réécrire le membre de gauche
m
d
V = −mg
dt
On peut dès lors simplifier par la masse (différente de zéro)
d
V = −g
dt
Le membre de droite est une constante, c'est-à-dire une puissance nulle de la variable
indépendante t. On peut donc intégrer directement
V ( t ) = − gt + C
où C représente une constante arbitraire dont on détermine la valeur à partir des conditions
initiales du problème. Ici, il convient d'exprimer l'annulation de la vitesse initiale, soit
0 = 0+C
La première constante d'intégration est donc nulle et on a
V ( t ) = − gt
Pour trouver la trajectoire, il faut se souvenir que
V (t ) =
dh
dt
où h représente la hauteur à laquelle se trouve le corps dans le repère défini précédemment.
1
Le corps est « lâché », c'est à-dire que sa vitesse de départ est nulle. Dans le cas contraire il serait « lancé ».
On doit donc encore résoudre
dh
= − gt
dt
qui s'intègre en
gt 2
h (t ) = −
+ C′
2
À nouveau, les conditions initiales permettent de déterminer la valeur de la constante C' : au
départ, le corps se trouve à l'origine et donc
0 = 0 + C′
La solution de l'équation de mouvement s'écrit donc
gt 2
h (t ) = −
2
5.6. Une relation d'ordre
Si f1, f2 et f3 sont intégrables sur l'intervalle ]a,b[, avec éventuellement a = –∝ ou b = ∝ ou les
deux, et liés par la relation
f1 ( x ) ≤ f 2 ( x ) ≤ f 3 ( x )
alors
b
∫
a
b
b
a
a
f1 ( x ) dx ≤ ∫ f 2 ( x ) dx ≤ ∫ f 3 ( x ) dx