Chapitre 2 Arithmétique et congruences

Chapitre 2
Arithmétique et congruences
L’arithmétique est la branche des mathématiques qui étudie les différentes questions
relatives à l’ensemble des nombres entiers (l’ensemble Z = {. . . ; −2; −1; 0; 1; 2; . . .}), notamment la problématique de la divisibilité. Elle est un des domaines scientifiques les
plus anciens. Ses problèmes internes ont motivé durant des siècles des développements
fondamentaux dans diverses parties des mathématiques. Plus récemment, des problèmes
concrets liés à l’informatique, l’électronique ainsi qu’à la représentation, la compression,
l’intégrité et la confidentialité des données, ont été résolus dans le cadre de l’arithmétique.
2.1
Division euclidienne
Le théorème suivant, sur lequel repose une partie de l’arithmétique, reprend la notion
de division euclidienne (c’est-à-dire avec quotient et reste) telle qu’on l’apprend à l’école
primaire.
Théorème 2.1 (Division euclidienne)
Soient a, b ∈ N avec b > 0. Il existe q, r ∈ N tels que l’on ait :
1. a = b · q + r,
2. 0 6 r < b.
De plus, q et r sont uniques pour cette propriété.
Définition 2.1
L’opération qui à a et b associe q et r vérifiant a = bq + r et 0 6 r < b s’appelle la
division euclidienne (ou division entière) de a par b. Dans cette opération, on dit que
a est le dividende, b le diviseur, q le quotient et r le reste.
Si on prend a, b, c et d appartenant à Z, on doit modifier un peu le théorème 2.1.
Théorème 2.2
Soient a, b ∈ Z avec b 6= 0. Il existe q, r ∈ Z tels que l’on ait :
1. a = b · q + r,
2. 0 6 r < |b|.
De plus, q et r sont uniques pour cette propriété.
1
App. des mathématiques, SAM
1ère année
2.2. Multiple et diviseur
Exemples
a) A l’école primaire, on pratique la division euclidienne selon le schéma suivant :
1 6 3
− 1 4
2 3
− 2 1
2
7
2 3
On dit alors que 163 ÷ 7 = 23 Reste : 2. Ceci s’écrit plus proprement sous la
forme donnée par le théorème : 163 = 7 · 23 + 2.
b) 17 = 5 · 3 + 2.
Ici : a = 17 (le dividende), b = 5 (le diviseur), q = 3 (le
quotient) et r = 2 (le reste).
2.2
c) −17 = (−5) · 4 + 3.
Ici : a = −17, b = −5, q = 4 et r = 3.
d) 17 = (−5) · (−3) + 2.
Ici : a = 17, b = −5, q = −3 et r = 2.
e) −17 = 5 · (−4) + 3.
Ici : a = −17, b = 5, q = −4 et r = 3.
Multiple et diviseur
Définition 2.2 (Rappel)
Soient a et b deux nombres entiers non nuls (a, b ∈ Z), alors :
1. a est un multiple de b s’il existe un nombre entier q tel que a = b · q.
2. b est un diviseur de a s’il existe un nombre entier q tel que a = b · q.
On note b|a.
Exemples
a) 32 est un multiple de 8, car 32 = 4 · 8.
b) 7 est un diviseur de 21, car 21 = 7 · 3.
Remarques
a) Il est équivalent de dire que a est un multiple de b ou b est un diviseur de a.
b) Si b 6= 0, dire que b divise a signifie que, dans la division euclidienne de a par b, le
reste est nul.
c) On notera que tout entier n ∈ Z divise 0, que 0 ne divise que lui-même et que les
nombre 1 et −1 divisent tous les entiers.
d) Le signe des nombres n’a pas d’importance pour la relation de divisibilité. On a effet
les équivalences :
b|a ⇐⇒ −b|a ⇐⇒ b| − a ⇐⇒ −b| − a
e) Si a et b sont > 0, on note que b|a implique b 6 a.
Proposition 2.3
Soit n ∈ Z. On a les propriétés suivantes :
page 2
1ère année
App. des mathématiques, SAM
2.3. PPMC, PGDC et nombres premiers
1. Si n divise a et b, alors n divise a + b et a − b.
2. Si n divise a et si λ est un entier quelconque, alors n divise λa.
Ceci revient à dire que, si n divise a et b, alors n divise toute combinaison linéaire ua + vb
de a et b, avec u, v ∈ Z.
Démonstration. On démontre ici la première partie de la proposition. Les deux autres
parties de la proposition se démontrent de manière analogue.
Si n divise a et b, il existe qa et qb tels que :
a = n · qa
et
b = n · qb
Or, on peut écrire la somme de a et b comme :
a + b = n · qa + n · qb = n · (qa + qb )
comme qa + qb ∈ Z, n divise a + b.
2.3
PPMC, PGDC et nombres premiers
Définition 2.3 (Rappel)
1. Un multiple commun de plusieurs nombres entiers est un nombre entier qui est
multiple de chacun d’eux. Le plus petit multiple commun (positif) de plusieurs
nombres est appelé le ppmc de ces nombres. Pour deux nombres a et b, on le note
P P MC(a, b).
2. Un diviseur commun de plusieurs nombres entiers est un nombre entier qui est
diviseur de chacun d’eux. Le plus grand diviseur commun (positif) de plusieurs
nombres est appelé le pgdc de ces nombres. Pour deux nombres a et b, on le note
P GDC(a, b).
Exemples
a) 36 est le ppmc de 3, 9 et 12.
b) 8 est le pgdc de 16, 24 et 40.
Définition 2.4
Un nombre entier naturel p est premier s’il admet exactement deux diviseurs, 1 et luimême.
Remarques
1. Convention : on déclare que le nombre 1 n’est pas un nombre premier.
2. Voici les 18 premiers éléments de l’ensemble des nombres premiers :
P = {2; 3; 5; 7; 11; 13; 17; 19; 23; 29; 31; 37; 41; 47; 53; 59; 61; . . .}
page 3
App. des mathématiques, SAM
1ère année
2.3. PPMC, PGDC et nombres premiers
Propriétés
1. Tout entier naturel n supérieur ou égal à 2 admet au moins un diviseur premier. De
plus, le plus petit diviseur de n différent de 1 est un nombre premier.
2. Il existe une infinité de nombres premiers.
Démonstration. Nous allons démontrer les 2 propriétés ci-dessus. On doit la deuxième
partie de la démonstration à Euclide.
1. Soit n un nombre naturel. Par l’absurde, supposons que le plus petit diviseur de n
différent de 1, noté d, n’est pas premier. Ainsi, n ne pourrait pas être premier non
plus (car si n est premier, alors son plus petit diviseur différent de 1 est lui-même) et
le fait que d divise n se traduirait par
n=d·q
avec 1 < d 6 q < n. En effet, d étant le plus petit diviseur de n différent de 1, on a
bien d 6 q. De plus, puisque d n’est pas premier, on a
d=a·b
avec 1 < a, b < d. Ainsi, on aurait
n=a·b·q
avec 1 < a, b < d 6 q. Ce qui montre que a et b seraient des diviseurs de n différents de
1 plus petits que d. C’est une contradiction avec le fait que d est le plus petit diviseur
de n différent de 1.
Ainsi, soit n est un nombre premier et son plus petit diviseur différent de 1 est luimême, soit n n’est pas premier et admet au moins un diviseur premier (au moins le
plus petit des diviseurs) différent de 1 et de lui-même.
2. Supposons que l’ensemble des nombres premiers soit fini. Il contient n nombres premiers p1 , p2 , . . . , pn .
Posons N = p1 · p2 · . . . · pn + 1. N n’est pas premier par hypothèse. N admet donc au
moins un diviseur premier pi qui doit être p1 , p2 , . . . ou pn : N = q · pi . Ainsi,
1 = N − p1 · p2 · . . . · pn = q · pi − p1 · p2 · . . . · pn
1 = pi (q − p1 · p2 · . . . · pi−1 · pi+1 · . . . · pn )
De 1 = pi (q −p1 · p2 · . . .· pi−1 · pi+1 · . . .· pn ), on tire que pi divise 1, ce qui est impossible.
Théorème 2.4 (Théorème fondamental de l’arithmétique)
Tout nombre entier naturel supérieur ou égal à 2 peut s’écrire comme un produit de
nombres premiers. Cette décomposition est unique à l’ordre des facteurs près.
On appelle cette décomposition la décomposition en facteurs premiers du nombre.
Exemples
- La décomposition de 720 en facteurs premiers est : 720 = 24 · 32 · 5.
- La décomposition de 4200 en facteurs premiers est : 4200 = 23 · 3 · 52 · 7.
page 4
1ère année
App. des mathématiques, SAM
2.3. PPMC, PGDC et nombres premiers
Définition 2.5
Soient a, b ∈ Z. On dit que a et b sont premiers entre eux si l’unique diviseur commun
de a et b (dans N) est 1.
Exemple
12 et 25 sont premiers entre eux.
Proposition 2.5
Soient a, b ∈ Z avec b 6= 0 et effectuons la division euclidienne de a par b :
a = b · q + r, avec 0 6 r < |b|.
1) Les diviseurs communs de a et b sont les mêmes que ceux de b et r.
2) On a P GDC(a, b) = P GDC(b, r).
Démonstration. La deuxième assertion résulte évidemment de la première. Pour celle-ci,
on note que si d divise a et b, il divise b et r = a − bq. De même, si d divise b et r, il
divise b et a = bq + r.
2.3.1
Algorithme d’Euclide (recherche du PGDC)
Cet algorithme permet de déterminer le PGDC de deux nombres a et b en effectuant
plusieurs divisions euclidiennes où à chaque étape le diviseur est remplacé par le reste
et le dividende par le diviseur. On arrête les divisions quand le reste est nul, le dernier
diviseur est le PGDC.
Algorithme d’Euclide
Données : Deux entiers a et b non nuls (a, b ∈ Z), avec |a| > |b|.
Résultat : Le plus grand diviseur commun de a et b : d = P GDC(a, b).
(1) Initialisation : On effectue la division de a par b : a = bq0 + r avec 0 6 r < |b|.
On pose r0 := b et r1 := r.
On pose également i := 1.
(2) Tant que ri 6= 0 faire :
(2.1) Effectuer la division euclidienne ri−1 = ri qi + ri+1 avec 0 6 ri+1 < ri .
(2.2) Poser i := i + 1.
(3) Retourner d = |ri−1 | comme résultat.
Cet algorithme est correct car d = P GDC(a, b) = P GDC(r0 , r1 ) = P GDC(r1, r2 ) =
P GDC(r2, r3 ) = . . .. De plus, comme 0 6 ri+1 < ri < . . . < r2 < r1 < r0 , on voit que l’on
obtient nécessairement un reste nul au bout d’au plus r0 opérations. Si on désigne par rn le
dernier reste non nul, on a donc rn−1 = rn qn . Ainsi rn |rn−1 et d = P GDC(rn−1, rn ) = rn .
page 5
1ère année
2.4. Identité de Bézout, algorithme d’Euclide étendu
App. des mathématiques, SAM
Exemple
On cherche à déterminer le PGDC de 8′ 172 et
on trouve :
a
b
q
8172 = 1650 · 4
1650 = 1572 · 1
1572 = 78 · 20
78 = 12 · 6
12 =
6
· 2
1′ 650. En appliquant l’algorithme,
r
+ 1572
+ 78
+ 12
+
6
+
0
Ainsi, P GDC(8′172, 1′650) = 6.
Comme 8′ 172 · 1′ 650 = 13′ 483′ 800, on a P P MC(8′ 172, 1′650) = 2′ 247′ 300.
2.4
Identité de Bézout, algorithme d’Euclide étendu
2.4.1
Identité de Bézout
Théorème 2.6
Soient a et b deux entiers relatifs non nuls et P GDC(a, b) leur PGDC.
Il existe deux entiers u et v tels que
u · a + v · b = P GDC(a, b)
(P GDC(a, b) est une combinaison linéaire de a et b, à coefficients entiers).
Démonstration. Par l’algorithme d’Euclide, on a que :
r1 = a − b · q0
r2 = b − r1 · q1
r3 = r1 − r2 · q2
...
rn−1 = rn−3 − rn−2 · qn−2
P GDC(a, b) = rn−2 − rn−1 · qn−1
Dans cette dernière relation, il suffit de substituer à rn−1 sa valeur dans l’avant-dernière
relation et de procéder de façon analogue avec rn−2 , rn−3 , . . .
2.4.2
Algorithme d’Euclide étendu
Définition 2.6
On appelle algorithme d’Euclide étendu la recherche de u et v.
Exemple
En reprenant les nombres 8172 et 1650 :
a
8172
1650
1572
78
12
=
=
=
=
=
b
1650
1572
78
12
6
·
·
·
·
·
q
4
1
20
6
2
page 6
+
+
+
+
+
r
1572
78
12
6
0
(1)
(2)
(3)
(4)
App. des mathématiques, SAM
1ère année
2.4. Identité de Bézout, algorithme d’Euclide étendu
De (4), on tire que 6 = 78 − 12 · 6.
De (3), on tire que 6 = 78 − (1572 − 78 · 20) · 6 = (−6) · 1572 + 121 · 78.
De (2), on tire que 6 = (−6) · 1572 + 121 · (1650 − 1572) = 121 · 1650 − 127 · 1572.
De (1), on tire que 6 = 121·1650−127·(8172−1650·4) = (−127)·8172+629·1650.
On a finalement u = −127 et v = 629.
On peut également écrire cet algorithme sous la forme d’un tableau à quatre colonnes : la
première colonne correspond aux restes obtenus par l’algorithme d’Euclide ; la dernière
colonne est celle des quotients. Dans les deux colonnes du milieu, on place (de gauche à
droite et de haut en bas) les nombres 1, 0, 0, 1. On peut choisir de remplir le tableau
colonne par colonne en commençant par la première et la dernière colonne, on peut aussi
remplir le tableau ligne par ligne. Les trois premières colonnes se construisent de manière
similaire : on calcule le nombre suivant à l’aide des deux nombres qui se trouvent juste
au-dessus et le quotient comme montré ci-dessous. L’algorithme est terminé lorsqu’on a
rempli la ligne du reste nul.
restes
a· ...
b· ...
quotients
a
1
0
b
0
1
q1
···
···
···
···
ri−1
si
ti
qi
ri
ui
vi
qi+1
ri+1 = ri−1 − ri qi+1 si − ui qi+1 ti − vi qi+1
qi+2
···
···
···
···
rn−1 = P GDC(a, b)
sn
tn
qn
rn = 0
un
vn
On peut associer les trois premières colonnes de chaque ligne de la manière suivante :
première colonne = a · deuxième colonne + b · troisième colonne
On trouve ainsi à l’avant-dernière ligne la combinaison de Bézout cherchée et un ”bonus”
à la dernière ligne.
P GDC(a, b) = sn · a + tn · b
et
0 = un · a + vn · b
Exemple
En reprenant à nouveau les nombres 8172 et 1650, on a :
restes 8172 · . . . 1650 · . . . quotients
8172
1
0
1650
0
1
4
1572
1
−4
1
78
−1
5
20
12
21
−104
6
6
−127
629
2
0
275
−1362
Par les deux dernières lignes, on obtient les deux identités :
P GDC(8172, 1650) = 6 = (−127) · 8172 + 629 · 1650
0 = 275 · 8172 + (−1362) · 1650
page 7
1ère année
App. des mathématiques, SAM
2.4.3
2.5. Equations diophantiennes
Lemme de Gauss
Théorème 2.7
Soient a et b deux nombres entiers.
Si c est un nombre tel que P GDC(c, a) = 1 et tel que c divise ab, alors c divise b.
Démonstration. Par le théorème de Bézout, il existe deux nombres entiers x et y tels que
x·c+y·a=1
En multipliant cette équation par b, on obtient :
x
c · }b + y · a · b = b
| ·{z
| {z }
divisible par c
Donc b est divisible par c.
2.5
divisible par c
Equations diophantiennes
Nous connaissons des méthodes qui permettent de résoudre des équations avec des solutions réelles. Or, parfois, nous avons besoin de résoudre des problèmes qui ne peuvent
admettre que des solutions à valeur entière, comme le problème suivant.
Exemple
Un cinéma vend deux sortes de ticket : ceux à 12 CHF et ceux à 17 CHF.
Un soir la caissière constate qu’elle a encaissé 285 CHF, mais elle ne se souvient
pas du nombre de billets de chaque sorte qu’elle a vendus.
Est-il possible de le lui dire ? Et si le ticket le plus cher valait 18 CHF ?
Définition 2.7
Soit a, b et c trois nombres entiers.
L’équation a · x + b · y = c est une équation diophantienne si les solutions cherchées
x et y sont des nombres entiers.
Résultat d’existence d’une solution
Soient a et b deux nombres entiers. On a l’équivalence :
a · x + b · y = c admet (au moins) une solution entière ⇐⇒ P GDC(a, b) divise c
Démonstration. On démontre chaque sens de l’équivalence.
“⇒” Il est évident que P GDC(a, b) divise a · x et b · y. Il divise donc leur somme qui
vaut c (car x et y sont solutions entières de l’équation ax + by = c).
“⇐” Par le théorème de Bézout, il existe deux nombres entiers m et n tels que :
a · m + b · n = P GDC(a, b)
Ces deux nombres entiers m et n se trouvent grâce à l’algorithme d’Euclide étendu.
page 8
1ère année
App. des mathématiques, SAM
2.5. Equations diophantiennes
Par hypothèse, il existe p ∈ Z tel que P GDC(a, b) · p = c (⇔ p =
en multipliant l’équation ci-dessus par p, on obtient :
c
).
P GDC(a,b)
Ainsi
a · (m · p) + b · (n · p) = pgcd(a, b) · p = c
On a donc trouvé une solution entière pour x et pour y.
x=m·p =
m·c
P GDC(a, b)
et
y =n·p=
n·c
P GDC(a, b)
Remarque
Avant de résoudre une équation diophantienne, on vérifie toujours si elle admet une
solution en utilisant ce résultat d’existence. En effet, si l’équation n’admet pas de solution,
le problème est alors terminé.
Solution particulière d’une équation diophantienne
Dans le cas où l’existence d’une solution est vérifiée, on peut commencer à chercher les
solutions de l’équation diophantienne.
La méthode de recherche d’une solution particulière se trouve dans la preuve du résultat
de l’existence d’une solution de l’équation diophantienne.
1. Grâce à l’algorithme d’Euclide étendu, on trouve une solution particulière (m; n) de
l’équation a · x + b · y = P GDC(a, b).
2. Pour trouver une solution particulière (x0 ; y0) de l’équation a·x+b·y = c, on multiplie
c
. Ainsi
m et n par P GDC(a,b)
(x0 ; y0) =
c
c
m·
;n·
P GDC(a, b)
P GDC(a, b)
Solution générale d’une équation diophantienne
Lorsque P GDC(a, b) divise c, les solutions de l’équation diophantienne a · x + b · y = c
sont

b


 x = x0 − P GDC(a, b) · k
a


 y = y0 +
·k
P GDC(a, b)
où k ∈ Z et (x0 ; y0 ) est une solution particulière de l’équation diophantienne.
Remarques
1. A chaque solution correspond un unique k (le même pour les deux équations).
A chaque nombre k correspond une unique solution.
page 9
App. des mathématiques, SAM
1ère année
2.6. Systèmes de numération
2. Les deux dernières lignes de l’algorithme d’Euclide étendu sous forme de tableau sont
très intéressantes pour la résolution d’une équation diophantienne.
restes
a· ...
b· ...
quotients
a
1
0
b
0
1
q1
···
···
···
···
P GDC(a, b)
m
n
qn
b
a
0
± P GDC(a,b)
± P GDC(a,b)
En effet, à l’avant-dernière ligne, on trouve une solution (m; n) de l’équation ax +
c
, on obtient une solution
by = P GDC(a, b). En multipliant cette solution par P GDC(a,b)
particulière de l’équation diophantienne ax + by = c.
A la dernière ligne, on trouve (au signe près) les coefficients de k de la solution générale
de l’équation diophantienne.
3. Ces résultats sont donnés sans preuve.
Exemple
On désire résoudre l’équation diophantienne 40 · x + 24 · y = 16.
1. On commence par vérifier si l’équation admet au moins une solution.
C’est bien le cas car P GDC(40, 24) = 8 divise 16.
2. Pour trouver la solution générale, on commence par appliquer l’algorithme d’Euclide étendu.
restes 40 · . . . 24 · . . . quotients
40
1
0
24
0
1
1
16
1
−1
1
8
−1
2
2
0
3
−5
Ainsi, d’après l’avant-dernière ligne, (−1; 2) est une solution particulière de
l’équation 40x + 24y = 8 = P GDC(40, 24) (en effet : 40 · (−1) + 24 · 2 = 8).
(−2; 4) est une solution particulière de 40x + 24y = 16. En effet, on trouve cette
16
= 2 la solution ci-dessus.
solution en multipliant par P GDC(40,24)
En utilisant la dernière ligne, on peut directement donner la solution générale
de l’équation diophantienne 40x + 24y = 16, qui est
x = −2 − 3 · k
y = 4 + 5·k
avec k ∈ Z. (On a bien :
2.6
b
P GDC(a,b)
=
24
8
= 3 et
a
P GDC(a,b)
=
40
8
= 5.)
Systèmes de numération
1, 2, 3, 4, 5, 6, 7, 8, 9 . . . comment en est-on arrivé là ? Pas si simple ! . . . et pour répondre
en quelques mots à cette question, nous allons devoir voyager de la Mésopotamie (actuel
Irak) à l’Afrique du Nord en passant par l’Egypte, l’Inde et la Grèce.
page 10
App. des mathématiques, SAM
2.6.1
1ère année
2.6. Systèmes de numération
Du sens du nombre à la numération
Pour commencer, il faut distinguer deux notions :
Le sens du nombre : faculté de remarquer, dans un ensemble d’objets identiques, que
l’un de ceux-ci a été enlevé ou ajouté. Cette faculté a été trouvée chez certains
animaux et chez certaines tribus primitives ne sachant pas compter à proprement
parler. Par exemple, les corbeaux et les pies sont capables de remarquer qu’un ou
des oeufs ont été enlevés de leur nid, si au départ il n’y avait pas plus de 4 oeufs. On
dit que ces oiseaux ont un sens du nombre de 4. Chez l’homme (tribus primitives),
il se situe entre 4 et 7.
La numération : faculté intellectuelle qui exige le passage par plusieurs degrés d’abstraction. Elle n’est observée que chez l’homme.
Le passage du sens du nombre à la numération demande, en théorie, le passage par 4
étapes d’abstraction successives :
Etape 1 : Il faut pouvoir comparer deux ensembles d’objets par une bijection (correspondance un à un). Il faut ensuite pouvoir faire abstraction de la nature des objets.
On peut alors faire le choix d’un système de référence. Par exemple, une petite
légende autour du mot ”calcul” (qui vient de ”calculus”, en latin, caillou), nous raconte que le berger déposait dans un panier autant de cailloux que de moutons qui
quittaient la bergerie. En rentrant des prés, le berger sortait les cailloux du panier
afin de vérifier le compte de moutons. Cette association est la base de tout système
de numération et permet en particulier de comparer la taille des ensembles.
Etape 2 : Ensuite, on passe à un groupement d’unités, puis à un groupement de groupements, pour limiter la grandeur du système de référence. Avec ce procédé, on
introduit une base du système. Par exemple, notre berger pourrait choisir de ranger les cailloux dans des paniers plus grands et ne plus compter tous les cailloux
mais uniquement les paquets de cailloux. C’est ce que nous faisons pour compter
de la monnaie : on construit des piles de dix pièces puis on compte uniquement le
nombre de piles. Les bases les plus fréquemment utilisées sont : 2, 5, 10, 20 et 60.
Etape 3 : Avec l’apparition de la base et de l’écriture, on peut transcrire les nombres.
Il faut introduire des symboles pour les écrire. On peut ici mettre en évidence 3
stades d’évolution :
1. On associe à chaque puissance de la base un symbole différent. Un nombre est
formé par la juxtaposition de symboles répétés autant de fois qu’il le faut et sa
valeur est alors égale à la somme des symboles qui le composent. Ce système
porte le nom de système de numération additif. Pour noter le chiffre 9 par
exemple, les égyptiens répètent neuf fois le symbole de l’unité.
Ce système a deux inconvénients majeurs :
– la longueur de la transcription du nombre,
– pour chaque nouvelle puissance de la base, il faut trouver un nouveau symbole.
2. On introduit des nouveaux symboles pour compter les différentes puissance
de la base. Pour comprendre, le nombre 932 représenté dans un tel type de
numération s’écrirait : 9100 310 21. On fait intervenir simultanément le multiplication et l’addition dans ce principe.
3. On supprime le symbole pour la puissance de la base. La place d’un symbole par rapport aux autres détermine sa valeur. On obtient un système de
page 11
App. des mathématiques, SAM
1ère année
2.6. Systèmes de numération
numération de position. C’est un système de ce type que nous utilisons
actuellement.
Etape 4 : Pour qu’un système de numération de position soit complet, il faut introduire
un nouveau symbole pour désigner une place vide lorsqu’on supprime les symboles
des puissances de la base. On voit ainsi apparaı̂tre le ”zéro”. On peut suivre son
évolution à travers les langues. Les Hindous (sanscrit) l’ont désigné par le mot
”sunya” qui signifie : vide ou nul. Les Arabes l’ont repris en le transformant quelque
peu pour donner ”sifr”. Enfin, les Européens (en latin) ont transformé ”sifr” en
”zephirum” qui donnera zéro et en ”cifra” qui donnera chiffre. Par l’évolution des
mots, on suit également le parcours du système décimal jusqu’à nos jours.
L’évolution dans la pratique n’a pas toujours suivi ce chemin. Elle peut être bien différente. Elle dépend :
– de la langue (structure, évolution),
– de la présence d’anciennes bases,
– du matériau d’écriture (pierre, argile, papyrus),
– d’événements politiques.
Remarques
1. On donne en annexe à ce chapitre quelques exemples de systèmes de numération.
2. Quelques dates comme repères :
30’000 av. J.C. : os de loup entaillé avec 55 incisions, retrouvé en Slovaquie.
-5’000 à -3’000 : numération orale dépassant le millier.
-3’000 av. J.C. : premières numérations écrites.
Vers 600 : premier système de position.
2.6.2
Ecriture d’un entier en base b
Définition 2.8
Une base de numération est un entier supérieur ou égal 2. Soit b une base de numération, le système de numération est doté de b chiffres allant de 0 à b − 1.
Le système de numération le plus couramment utilisé est le système décimal (b = 10),
fondé sur les mathématiques indiennes. Un autre système très important est le système
binaire (b = 2) qui est utilisé par les ordinateurs (car ceux-ci ne travaillent qu’avec deux
chiffres : 0 et 1). En informatique, on se sert parfois également du système octal (b = 8)
ou du système hexadécimal (b = 16). Dans ce dernier cas, les chiffres supérieurs à 9 sont
représentés par les lettres de A à F.
Les Babyloniens utilisaient le système sexagésimal (b = 60), ainsi que les Indiens et les
Arabes en trigonométrie. Nous utilisons encore ce système aujourd’hui dans la mesure
du temps et des angles. Le système vigésimal (b = 20) a été utilisé par les Basques, les
Mayas, et peut-être les Gaulois (il s’agit là d’une simple hypothèse). Certains historiens
estiment que la civilisation de la vallée de l’Indus utilisait initialement un système octal
(b = 8).
Théorème 2.8 (Ecriture d’un entier dans une base b)
Soit b ∈ N, b > 2. Tout entier a > 0 s’écrit de manière unique sous la forme
a = an bn + · · · + a2 b2 + a1 b + a0
page 12
1ère année
App. des mathématiques, SAM
2.6. Systèmes de numération
avec n > 0, ai ∈ N, 0 6 ai < b et an 6= 0.
L’unicité signifie que si on a
a = an bn + · · · + a2 b2 + a1 b + a0 = a′m bm + · · · + a′2 b2 + a′1 b + a′0
alors on a m = n et ai = a′i pour tout i = 0, 1, . . . , n.
Cette écriture s’appelle l’écriture en base b de a et les ai sont les chiffres. La place de
ces symboles indique le poids qui leur est affecté (poids 1, poids b, poids b2 , . . . ).
Nous utiliserons la convention d’écriture suivante.
Lorsque la base est 10, nous noterons, comme il est d’usage, a = an . . . a1 a0 .
Lorsque la base est différente de 10 nous noterons a = an . . . a1 a0 . Dans certains livres,
on trouve également la notation a = (an . . . a1 a0 )b qui permet d’expliciter directement la
base dans laquelle on travaille.
Exemple
D’après ce théorème, le nombre 6754 exprimé en base 8 représente l’entier (en base
10) :
6754 = 6 × 83 + 7 × 82 + 5 × 8 + 4 = 3564
De même, le nombre 10001001 exprimé en base 2 représente l’entier (en base 10) :
1001001 = 1 × 27 + 1 × 23 + 1 = 137
Démonstration. Nous allons utiliser le principe de récurrence pour démontrer l’existence
de l’écriture. Plus précisément, on considère la propriété E(N) suivante, pour N > 0 :
Tout entier vérifiant 0 < a 6 N s’écrit sous la forme
a = an bn + · · · + a2 b2 + a1 b1 + a0
(2.1)
avec les conditions du théorème 2.8 : n > 0, 0 6 ai < b et an 6= 0.
La propriété est évidente pour tous les entiers N < b. En effet, si on a 0 < a 6 N < b,
on écrit a sous la forme (2.1) en prenant n = 0 et a0 = a. On a effectué ici l’ancrage de
notre preuve par récurrence.
Supposons que E(N) soit vraie (avec N > b − 1) et montrons que E(N + 1) l’est aussi.
Grâce à l’hypothèse que E(N) est vraie, il ne reste plus qu’à écrire N + 1 sous la forme
(2.1).
Pour cela, on divise N + 1 par b (division euclidienne) ce qui donne N + 1 = bq + r avec
0 6 r < b. Comme N + 1 est > b, on a q > 0. On en déduit également que q < N + 1,
donc q 6 N. Comme E(N) est vraie, q s’écrit sous la forme (2.1) :
q = cm bm + · · · + c1 b + c0
avec m > 0 et 0 6 ci < b et cm 6= 0. On en déduit aussitôt qu’on a
N + 1 = bq + r = cm bm+1 + · · · + c1 b2 + c0 b + r
ce qui est une écriture de N + 1 sous la forme (2.1).
page 13
App. des mathématiques, SAM
1ère année
2.7. Congruences
Montrons maintenant l’unicité. On raisonne encore par récurrence en considérant la propriété U(N) suivante :
Si un entier a 6 N admet deux écritures :
a = an bn + · · · + a2 b2 + a1 b + a0 = a′m bm + · · · + a′2 b2 + a′1 b + a′0 ,
(2.2)
on a m = n et ai = a′i pour tout i = 0, 1, . . . , n.
La propriété est évidente pour N < b. En effet, si on a a 6 N < b avec deux écritures,
on a m = n = 0 (sinon a est > b) et a = a0 = a′0 , donc les écritures sont les mêmes.
Supposons que U(N) soit vraie (avec N > b − 1) et montrons que U(N + 1) l’est aussi. Il
reste juste à examiner le cas N + 1. Supposons donc qu’on ait deux écritures de a = N + 1
comme en (2.2) ci-dessus. L’écriture de N + 1 montre que a0 est le reste de la division de
N + 1 par b et il en est de même pour a′0 . Par unicité du reste, on a donc déjà a0 = a′0 .
En retranchant a0 ou a′0 et en divisant par b, on en déduit que l’entier
q = an bn−1 + · · · + a2 b + a0 = a′m bm−1 + · · · + a′2 b + a′1
(qui est le quotient de la division) admet deux écriture en base b. On montre, comme
dans la démonstration de l’existence, que cet entier q est 6 N. D’après l’hypothèse de
récurrence U(N), les deux écritures sont donc les mêmes et on a n = m et ai = a′i pour
tout i = 1, . . . , n, ce qui, avec a0 = a′0 , achève la démonstration.
2.7
Congruences
Définition 2.9
Soit n un nombre naturel strictement positif (n ∈ N∗ ). Si a et b sont deux nombres entiers
(a, b ∈ Z), on dit que a est congru à b modulo n si n divise la différence b − a. On note :
a ≡ b (mod n).
a ≡ b (mod n) se lit : ”a est congru à b modulo n”.
Remarque
Par définition, si a ≡ b (mod n), n divise la différence b − a. Il existe donc k ∈ Z tel que
b − a = n · k. On a donc l’égalité :
b=a+n·k
Exemple
a) 19 ≡ 7 (mod 12), car 19 − 7 = 12 = 12 · 1
b) 1 ≡ −11 (mod 12), car −11 − 1 = −12 = 12 · (−1)
c) 32 ≡ −1 (mod 5), car −1 − 32 = −10 = 5 · (−2)
d) un entier n est pair si et seulement si n ≡ 0 (mod 2), et n est impair si et
seulement si n ≡ 1 (mod 2).
page 14
1ère année
App. des mathématiques, SAM
2.7. Congruences
Proposition 2.9
Soient a ∈ Z et n ∈ N, avec n > 0. Effectuons la division euclidienne de a par n :
a = nq + r
avec 0 6 r < n
Alors, on a a ≡ r (mod n).
Remarque
Comme chaque entier a s’écrit de façon unique a = nq + r avec 0 6 r < n, deux entiers a
et a′ sont congrus modulo n si et seulement s’ils admettent le même reste r par division
euclidienne par n.
Proposition 2.10
Soit n > 2 un nombre entier et soient a, b, c, d ∈ Z. Les affirmations suivantes sont
correctes.
1. Compatibilité de la loi + avec la congruence modulo n :
a≡b
(mod n) et c ≡ d (mod n) =⇒ a + c ≡ b + d (mod n).
2. Compatibilité de la loi · avec la congruence modulo n :
a ≡ b (mod n) et c ≡ d
(mod n) =⇒ a · c ≡ b · d
(mod n).
De plus, si a ≡ b (mod n) et c ≡ d (mod n) alors ax + cy ≡ bx + dy (mod n) pour
tout x, y ∈ Z.
3. Pour tout entier strictement positif k (k ∈ N),
a ≡ b (mod n) =⇒ ak ≡ bk
(mod n).
4. Si f (x) = a0 + a1 x + a2 x2 + . . . + am xm est un polynôme de degré m avec a0 , a1 , . . . ,
am ∈ Z et si a ≡ b (mod n) alors f (a) ≡ f (b) (mod n).
Démonstration. Nous allons démontrer les propositions 1 et 2. Les propositions 3 et 4
découlent des deux premières.
Soit n > 2 un nombre entier et soient a, b, c, d ∈ Z tels que a ≡ b (mod n) et c ≡ d
(mod n). Par définition, il existe p ∈ Z et q ∈ Z tels que
b−a=n·p
et
d−c=n·q
1. Pour montrer que a + c ≡ b + d (mod n), on montre que (b + d) − (a + c) est divisible
par n :
(b + d) − (a + c) = (b − a) + (d − c) = n · p + n · q = n · (p + q)
Comme p + q ∈ Z, la congruence est démontrée.
page 15
1ère année
App. des mathématiques, SAM
2.7. Congruences
2. Pour montrer que a · c ≡ b · d (mod n), on montre que (b · d) − (a · c) est divisible par
n:
(b · d) − (a · c) = ((a + n · p) · (c + n · q)) − (a · c)
= a · c + a · n · q + n · p · c + n2 · p · q − a · c
= n · (a · q + c · p + n · p · q)
Comme a · q + c · p + n · p · q ∈ Z, la congruence est démontrée.
Exemple
On va montrer que 7|(3 · 2101 + 9).
En effet, on évite d’élever 2 à la puissance 101 en procédant comme suit. Comme
2101 = (23 )33 · 22 et 23 = 8 ≡ 1 (mod 7), on a, en utilisant les propriétés ci-dessus :
3 · 2101 + 9 ≡ 3(1)33 · 4 + 9 ≡ 12 + 9 ≡ 0
en travaillant modulo 7.
Proposition 2.11
Soit n > 2 un nombre entier et soient a, b, c ∈ Z. Les affirmations suivantes sont correctes
(toutes les congruences sont modulo n).
1. a ≡ a (relation réflexive).
2. a ≡ b ⇐⇒ b ≡ a (relation symétrique).
3. si a ≡ b et si b ≡ c =⇒ a ≡ c (relation transitive).
Ceci implique que le relation de congruence est une relation d’équivalence sur Z.
Définition 2.10
Soit n > 2 un nombre entier et soit a ∈ Z.
On appelle classe de a modulo n l’ensemble des entiers congrus à a modulo n.
Sachant que deux nombre a et b sont congrus modulo n si et seulement s’ils ont le même
reste dans la division par n, les n restes possibles permettent de définir n classes modulo
n. Ceci définit une partition de Z en n classes distinctes, les classes de 0, 1, 2, . . . , n − 1.
On désigne par Z/nZ ou Zn l’ensemble quotient formé par ces n classes.
Exemple
Pour n = 5, on peut classer les nombres entiers selon leurs congruences modulo 5 :
. . . ≡ −15 ≡ −10 ≡ −5 ≡ 0 ≡ 5 ≡ 10 ≡ 15 ≡ 20 ≡ 25 ≡ . . .
. . . ≡ −14 ≡ −9 ≡ −4 ≡ 1 ≡ 6 ≡ 11 ≡ 16 ≡ 21 ≡ 26 ≡ . . .
. . . ≡ −13 ≡ −8 ≡ −3 ≡ 2 ≡ 7 ≡ 12 ≡ 17 ≡ 22 ≡ 27 ≡ . . .
. . . ≡ −12 ≡ −7 ≡ −2 ≡ 3 ≡ 8 ≡ 13 ≡ 18 ≡ 23 ≡ 28 ≡ . . .
. . . ≡ −11 ≡ −6 ≡ −1 ≡ 4 ≡ 9 ≡ 14 ≡ 19 ≡ 24 ≡ 29 ≡ . . .
On a obtenu cinq classes notées 0̇, 1̇, 2̇, 3̇, 4̇. On a alors que Z5 = {0̇; 1̇; 2̇; 3̇; 4̇}
On notera abusivement que Z5 = {0; 1; 2; 3; 4}.
page 16
1ère année
App. des mathématiques, SAM
2.7. Congruences
Opérations dans Zn
Définition 2.11
On peut définir une addition et multiplication dans Zn .
Si on considère ȧ et ḃ deux classes d’équivalence de Zn , alors
˙ b).
ȧ + ḃ = (a +
1. l’addition est définie par :
ȧ · ḃ = (a ˙· b)
2. la multiplication est définie par :
Autrement dit, on définit la somme modulo n des classes de a et b comme étant la classe
˙ b) de la somme arithmétique de a et de b (donnée par a + b). On définit le produit
(a +
modulo n des classes de a et de b comme étant la classe (a ˙· b) du produit arithmétique
de a et de b (donnée par a · b).
Exemples
–
–
–
–
Modulo
Modulo
Modulo
Modulo
5, on a : 3̇ + 4̇ = 2̇.
13, on a : 7̇ + 9̇ = 3̇.
5, on a : 2̇ · 4̇ = 3̇.
6, on a : 3̇ · 4̇ = 0̇.
Les opérations définies ci-dessus dans Zn ont les propriétés suivantes.
Propriétés de l’addition
1) L’addition est commutative :
ȧ + ḃ = ḃ + ȧ
2) L’addition est associative :
ȧ + (ḃ + ċ) = (ȧ + ḃ) + ċ
3) La classe 0̇ est l’élément neutre :
˙ est l’élément opposé de ȧ :
4) La classe de −a, (−a),
ȧ + 0̇ = ȧ
˙ = 0̇
ȧ + (−a)
Propriétés de la multiplication
1) La multiplication est commutative :
ȧ · ḃ = ḃ · ȧ
2) La multiplication est associative :
ȧ · (ḃ · ċ) = (ȧ · ḃ) · ċ
3) 1̇ est l’élément neutre :
1̇ · ȧ = ȧ
La multiplication est distributive par rapport à l’addition
ȧ · (ḃ + ċ) = ȧ · ḃ + ȧ · ċ
Exemple
Dans Z5 , on a bien que
4̇ · (1̇ + 2̇) = 2̇ = 4̇ · 1̇ + 4̇ · 2̇
car
– 4 · (1 + 2) ≡ 2 (mod 5)
– 4 · 1 + 4 · 2 ≡ 2 (mod 5)
Ces propriétés découlent directement des propriétés de l’addition et de la multiplication
dans Z.
page 17
App. des mathématiques, SAM
2.8
1ère année
2.8. Critères de divisibilité
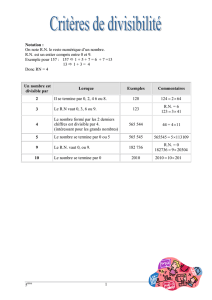
Critères de divisibilité
L’arithmétique modulaire offre un outil particulièrement efficace à l’établissement de
critères de divisibilité (déterminer si un entier a est divisible par un entier b revient en
effet à déterminer si a est congru à 0 modulo b).
Pour démontrer ces critères de divisibilité, il faut utiliser la representation d’un nombre
en base 10. Plus précisément, on va considérer a un nombre entier positif dont on écrit
la représentation en base 10 ainsi :
a = an 10n + . . . + a2 102 + a1 10 + a0
avec 0 < an 6 9 et 0 6 ak 6 9 pour k = 0, . . . , n − 1.
Divisibilité par 2
Un entier a est divisible par 2 si et seulement si son chiffre des unités est 0, 2, 4, 6 ou 8.
Divisibilité par 3
Un entier a est divisible par 3 si et seulement si la somme de ses chiffres est divisible par
3.
Démonstration. La représentation en base 10 de a est donnée par :
a = an 10n + . . . + a2 102 + a1 10 + a0
avec 0 < an 6 9 et 0 6 ak 6 9 pour k = 0, . . . , n − 1. Comme 10n ≡ 10n−1 ≡ . . . ≡ 10 ≡ 1
(mod 3) :
a ≡ an + an−1 + . . . + a1 + a0 (mod 3).
Ainsi, a ≡ 0 (mod 3) si et seulement si an + an−1 + . . . + a1 + a0 ≡ 0 (mod 3).
Divisibilité par 4
1) Un entier a est divisible par 4 si et seulement si le nombre formé par ses deux derniers
chiffres est divisible par 4.
2) Un entier a est divisible par 4 si et seulement si le chiffre obtenu en additionnant son
chiffre des unités au double de son chiffre des dizaines est divisible par 4.
Divisibilité par 5
Un entier a est divisible par 5 si et seulement si son chiffre des unités est 0 ou 5.
Divisibilité par 6
Un entier a est divisible par 6 si et seulement si la somme de ses chiffres est divisible par
3 et son chiffre des unités est pair.
page 18
App. des mathématiques, SAM
1ère année
2.8. Critères de divisibilité
Divisibilité par 7
1) Un entier a est divisible par 7 si et seulement si la somme de ses chiffres pris depuis
la droite et multipliés par 1,3,2,6,4,5,1,3,2,6,4,5,. . . est divisible par 7.
2) Un entier a est divisible par 7 si et seulement si le nombre obtenu en retranchant le
double de son chiffre des unités au nombre formé de ses autres chiffres est divisible
par 7.
Exemples
Soit a = 2′ 034.
1) 4 · 1 + 3 · 3 + 0 · 2 + 2 · 6 = 25. 2′ 034 n’est pas divisible par 7.
2) 203 − 8 = 195 ; 19 − 10 = 9. 2′ 034 n’est pas divisible par 7.
Soit a = 17′ 976.
1) 6 · 1 + 7 · 3 + 9 · 2 + 7 · 6 + 1 · 4 = 91 ; 91 : 1 · 1 + 9 · 3 = 28. 17′ 796 est divisible
par 7.
2) 1797 − 12 = 1785 ; 178 − 10 = 168 ; 16 − 16 = 0. 17′7961 est divisible par 7.
Divisibilité par 8
1) Un entier a est divisible par 8 si et seulement si le nombre formé de ses trois derniers
chiffres est divisible par 8.
2) Un entier a est divisible par 8 si et seulement si le nombre obtenu en additionnant son
chiffre des unités, le double de son chiffre des dizaines et le quadruple de son chiffre
des centaines est divisible par 8.
Exemple
Soit a = 17′ 976.
6 + 2 · 7 + 4 · 9 = 56. 17′ 976 est divisible par 8.
Divisibilité par 9
Un entier a est divisible par 9 si et seulement si la somme de ses chiffres est divisible par
9.
Divisibilité par 10
Un entier a est divisible par 10 si et seulement si son chiffre des unités est 0.
Divisibilité par 11
Un entier a est divisible par 11 si et seulement si la différence entre la somme de ses
chiffres de rang pairs et la somme de ses chiffres de rang impairs est divisible par 11.
Exemple
Soit a = 57′ 865′654.
4 − 5 + 6 − 5 + 6 − 8 + 7 − 5 = 0. 57′ 865′ 654 est donc divisible par 11.
page 19
1ère année
App. des mathématiques, SAM
2.9. Le jour de la semaine
Divisibilité par 12
Un entier a est divisible par 12 si et seulement si la somme de ses chiffres est divisible
par 3 et le nombre formé de ses deux derniers chiffres est divisible par 4.
Divisibilité par 13
Un entier a est divisible par 13 si et seulement si le nombre obtenu en additionnant le
quadruple de son chiffre des unités au nombre formé des autres chiffres est divisible par
13.
Exemples
Soit a = 2′ 114.
211 + 4 · 4 = 277 ; 22 + 4 · 7 = 40 qui n’est pas divisible par 13. 2′ 114 n’est donc pas
divisible par 13.
Soit a = 3′ 276.
327 + 4 · 6 = 351 ;35 + 4 · 1 = 39. 3′ 276 est donc divisible par 13.
2.9
Le jour de la semaine
Nous allons, dans cette partie, rechercher le jour de la semaine d’une date donnée. Cette
activité a comme fondement mathématique la congruence. Les problèmes relatifs au jour
de la semaine peuvent être résolus au moyen de claculs, de formules ou d’un ensemble de
tableaux appelé calendrier perpétuel.
Par la suite, on va considérer qu’une date est donnée sous la forme j/m/a avec j pour le
jour, m pour le mois et a pour l’année.
2.9.1
Formule de Zeller
L’algorithme établi par l’allemand Christian Zeller en 1885 permet de trouver le jour de
la semaine d’une date donnée.
Théorème 2.12 (Formule de Zeller)
Le jour J (un nombre entier entre 0 et 6 avec dimanche codé par 0, . . . ) correspondant à
la date j/m/a est donné par :
′
J ≡ j + [2.6m − 0.2] + e +
hei
4
+
hsi
4
− 2s (mod 7)
où :
– [·] désigne la partie entière,
(m − 2, a)
si m > 2
– (m′ , a′ ) =
(m + 10, a − 1) si m 6 2
– a′ = 100s + e, 0 6 e < 100.
Définition 2.12 (Rappel)
La partie entière de x est le plus grand entier inférieur ou égal à x, noté E(x) ou [x].
La partie fractionnaire de x est donnée par x − [x], noté {x}.
page 20
App. des mathématiques, SAM
1ère année
2.9. Le jour de la semaine
Exemple
– [3.4578] = 3 et {3.4578} = 0.4578.
– [0.0987] = 0 et {0.0987} = 0.0987.
– [−2.234] = −3 et {−2.234} = 0.766.
Plus simplement, la partie fractionnaire d’un nombre positif a est ce qui se trouve à droite
de la virgule.
Exemple
Le 20 août 1976 était un jeudi, car J est égal à 4. Voici le détail des calculs.
On a que : j = 20, m′ = 6, a′ = 1976, s = 19 et e = 76. On doit donc calculer :
76
19
20 + [2.6 · 6 − 0.2] + 76 +
+
− 2 · 19
4
4
Ce qui donne :
20 + 15 + 76 + 19 + 4 − 38 = 88
Or J ≡ 88 (mod 7) et 0 6 J < 7. Ainsi J = 4 (équivaut au reste de la division
euclidienne de 88 par 7). Et donc le 20 août 1970 était un jeudi.
Nous allons démontrer la formule de Zeller. Commençons par rappeler les propriétés du
calendrier grégorien, qui a été mis en place en 1582 par le pape Grégoire XIII : l’année
est de 365 jours, sauf quand elle est bissextile, c’est-à-dire quand l’année est divisible par
4, sauf les années séculaires (divisibles par 100), qui ne sont bissextiles que si divisibles
par 400.
Si j et m sont fixés, et comme 365 = 7 · 52 + 1, la quantité J avance de 1 d’année en
année, sauf quand la nouvelle année est bissextile, auquel cas, J progresse de 2. Il faut
donc déterminer le nombre d’années bissextiles inférieures à a.
Détermination du nombre d’années bissextiles
Proposition 2.13
Le nombre d’entiers de [1; N] qui sont divisibles par k est donné par ρ(N, k) = [ Nk ].
Démonstration. Les entiers m de l’intervalle [1, N] divisibles par k sont de la forme m =
kr avec 1 6 kr 6 N et donc k1 6 r 6 Nk . Comme r doit être entier, on a en fait
1 6 r 6 [ Nk ].
Proposition 2.14
Le nombre d’années bissextiles dans ]1600, a] est :
T (a) = ρ(a − 1600, 4) − ρ(a − 1600, 100) + ρ(a − 1600, 400)
h i h
h
a
1600
a i
1600
a i
1600
=
−
−
−
+
−
4
4
100
100
400
400
hai h a i h a i
=
−
+
− 388
4
100
400
Démonstration. On applique la définition des années bissextiles : toutes les années bissextiles sont divisibles par 4, sauf celles divisibles par 100 à moins qu’elles ne soient multiples
de 400.
page 21
1ère année
App. des mathématiques, SAM
2.9. Le jour de la semaine
Pour simplifier, on écrit a = 100s + e avec 0 6 e < 100, ce qui donne :
hei
hsi
T (a) =
+ 25s − s +
− 388.
4
4
Comme le mois de février a un nombre de jours variables, on décale l’année : on suppose
qu’elle va de mars à février. On passe de l’année (m, a) à l’année-Zeller (m′ , a′ ) comme
indiqué ci-dessus.
Détermination du jour du 1er mars
On doit maintenant déterminer le jour du 1er mars. Ce jour est le premier jour de l’année
Zeller.
On appelle µ(x) la fonction qui associe au nombre x le reste de la division euclidienne
par 7 (ce qui est équivalent à travailler modulo 7).
Supposons que le 1er mars 1600 soit le jour n de la semaine, alors il est µ(n + 1) en 1601,
µ(n + 2) en 1602, µ(n + 3) en 1603 et µ(n + 5) en 1604. De proche en proche, le 1er mars
de l’année a′ est donc :
M(a′ ) = µ(n + (a′ − 1600) + T (a′ ))
Maintenant, on détermine n à rebours en utilisant le fait que le 1er mars 2011 était un
mardi :
M(2011) ≡ 2 ≡ n + 2011 − 1600 + T (2011)
20
11
+ 24 · 20 +
− 388
≡ n + 411 +
4
4
≡ n + 510 ≡ n + 6 (mod 7)
On trouve n = 3.
Le premier jour des autres mois
On peut précalculer le décalage entre le jour du mois de mars et ses suivants :
1er
1er
1er
1er
1er
1er
1er
1er
1er
1er
1er
avril
mai
juin
juillet
août
septembre
octobre
novembre
décembre
janvier
février
1er
1er
1er
1er
1er
1er
1er
1er
1er
1er
1er
mars + 3
avril + 2
mai + 3
juin + 2
juillet + 3
août + 3
septembre + 2
octobre + 3
novembre + 2
décembre + 3
janvier + 3
Ainsi, si le premier mars d’une année est un vendredi, alors le 1er avril est un lundi, et
ainsi de suite.
On peut résumer le décalage donné par ce tableau par la formule [2.6m′ − 0.2] − 2, d’où :
page 22
App. des mathématiques, SAM
1ère année
2.9. Le jour de la semaine
Proposition 2.15
Le 1er du mois m′ est congru à
M(a′ ) + [2.6m′ − 0.2] − 2 ≡ 3 + 100s + e − 1600 + T (100s + e) + [2.6m′ − 0.2] − 2
hei hsi
≡ −1987 + 124s + e +
+
4h i 4h i
s
e
≡ 1 + [2.6m′ − 0.2] + e +
+
− 2s
4
4
modulo 7.
Et le résultat final en découle.
2.9.2
Formule de Kraitchik
L’algorithme établi par Maurice Kraitchik permet de trouver, comme l’algorithme de
Zeller, le jour de la semaine d’une date donnée.
Théorème 2.16 (Formule de Kraitchik)
Le jour J (un nombre entier entre 0 et 6 avec samedi codé par 0, . . . ) correspondant à la
date j/m/a est donné par :
hai h a i h a i
3(m′ + 1)
+a+
J ≡ j + 2m +
−
+
+ 2 (mod 7)
5
4
100
400
′
où :
– [·] désigne
la partie entière,
m
si m > 2
– m′ =
m + 12 si m 6 2
Exemple
Le 6 juillet 1900 était un vendredi, car J est égal à 6. Voici le détail des calculs.
On a que : j = 20, m′ = 7 et a = 1900. On doit donc calculer :
3(7 + 1)
1900
1900
1900
20 + 2 · 7 +
+ 1900 +
−
+
+2
5
4
100
400
Ce qui donne :
20 + 14 + 4 + 1900 + 475 − 19 + 4 + 2 = 2400
Or J ≡ 2400 (mod 7) et 0 6 J < 7. Ainsi J = 6. Et donc le 20 juillet 1900 était
un vendredi.
page 23
App. des mathématiques, SAM
2.10
1ère année
2.10. Exercices
Exercices
1) Appliquer l’algorithme d’Euclide pour déterminer le PGDC et le PPMC des nombres
a et b :
a) a = 528 et b = 312
b) a = 4725 et b = 3792
c) a = 26 et b = 19
d) a = 4350 et b = 2456
2) Démontrer le théorème fondamental de l’arithmétique (existence et unicité).
3) Déterminer deux nombres u et v tels que 144u + 55v = 1.
4) Les équations suivantes admettent-elles au moins une solution à coordonnées entières ?
a) 5x + 2y = 2731
b) 4999x + 3771y = 1
c) 6x + 4y = 5
5) Résoudre les équations diophantiennes :
a) 7x + 2y = 5
b) 217x + 34y = 2
c) 544x − 944y = 160
d) 65x + 104y = 26
e) 56x − 21y = 105
f) 14x + 20y = 7
g) 168x + 255y = 3
h) 84x + 35y = 150
i) 12x + 17y = 285
j) 45x + 5y = 12
6) Un magicien présente un tour. Il affirme qu’il peut deviner la date de naissance d’un
spectateur. Il lui dit :
”Prenez votre jour de naissance. Multipliez le par 31. Prenez votre mois de naissance.
Multiplier le par 12. Ajoutez ces deux nombres. Combien trouvez-vous ? 811 vous me
dites ? Et bien vous êtes né un 25 mars !”
En plus, c’est vrai. Mais comment a-t-il fait ?
7) Un cinéma vend deux sortes de tickets, ceux à 12 CHF et ceux à 17 CHF.
Un soir la caissière constate qu’elle a encaissé 285 CHF, mais elle ne se souvient pas
du nombre de billets de chaque sorte qu’elle a vendus.
a) Est-il possible de le lui dire ?
b) Qu’aurait-on pu lui dire si le prix des billets est de 12 CHF et de 18 CHF ?
8) Déterminer les points à coordonnées entières des droites suivantes :
a) 3x − 5y = 12
b) 39x + 91y = 113
page 24
App. des mathématiques, SAM
1ère année
2.10. Exercices
c) ax + by = c, a, b, c ∈ Z et c 6= 0
9) Transformer les entiers suivants, exprimés dans la base 10, en la base demandée :
a) 345
en base 4.
b) 782
en base 5.
c) 1234
en base 9.
d) 2765
en base 3.
e) 3452
en base 2.
f) 4567
en base 6.
g) 3245
en base 7.
h) 16324
en base 8.
10) Transformer les entiers suivants, exprimés dans la base b, en base 10 :
a) 1001001001
b = 2.
b) 8234
b = 9.
c) 12345
b = 6.
d) 61245
b = 8.
e) 126435
b = 7.
f) 444444
b = 5.
g) 2121210021
b = 3.
h) 123123123
b = 4.
11) Calculer :
a) 4 · 7 (mod 9)
b) 14 + 71 (mod 83)
c) 44 (mod 12)
d) 3 · 9 − 7 · 8 (mod 11)
e) 247349 (mod 7)
12) Calculer le reste de la division de :
a) 22148 + 1
par 33
b) 97108 − 12598
c) 2
1147
par 7
par 17
13) Montrer que :
a) 3457 − 1
b) 951842 − 4
est un multiple de 11.
est divisible par 5.
14) Démontrer les affirmations suivantes :
a) Le produit de 4 entiers consécutifs est toujours divisible par 24.
b) Quel que soit l’entier naturel n, n3 − n est divisible par 6.
c) Si n est impair alors n2 − 1 est divisible par 8.
d) Si m et n sont impairs, alors m2 + n2 est pair, mais non divisible par 4.
e) Quel que soit l’entier naturel n, 52n − 7n est divisible par 18.
f) Quel que soit l’entier naturel n, 32n+1 + 2n+2 est divisible par 7.
page 25
1ère année
App. des mathématiques, SAM
2.10. Exercices
15) Soit m ≥ 2 un entier et soient a, b, c, d ∈ Z. Démontrer les affirmations suivantes
(toutes les congruences sont modulo m) :
a) a ≡ a ;
b) a ≡ b si et seulement si b ≡ a ;
c) si a ≡ b et si b ≡ c alors a ≡ c.
16) Répondre aux questions suivantes.
a) Quel est le reste de la division par 5 de 4 · 11532 + 17 ?
b) Soit n un entier positif. Montrer que le chiffre des unités de n2 est l’un des nombres
suivants : 0, 1, 4, 5, 6 ou 9.
c) Quelles sont les valeurs possibles du chiffre des unités de 4m (où m ∈ N∗ ) ?
d) Soit n un entier ; démontrer que (n+1)3 −n3 n’est jamais divisible par 3. (Travailler
modulo 3.)
17) a) Réaliser les tables d’additions et de multiplications de Z2 , Z3 , Z4 , Z5 et Z6 .
b) Quels sont les éléments inversibles de Z2 , de Z3 , de Z4 , de Z5 et de Z6 ?
c) Trouver les éléments x de Z4 différents de 0̇ tels qu’il existe un élément y de Z4
différent de 0̇ où
x · y = 0̇
d) Même question que c) pour Z5 .
e) Même question que c) pour Z6 .
18) Résoudre les équations suivantes.
a) x2 + x + 1 = 0 dans Z4
b) x3 + 2x = 0 dans Z6
19) Montrer les critères de divisibilité par :
a) 4
b) 5
c) 8
d) 9
e) 11
20) Dans cet exercice, la somme des chiffres d’un nombre naturel non nul n est la somme
des chiffres de sa représentation décimale.
Un magicien présente un tour. Il invite un spectateur à faire les opérations suivantes
de tête :
(a) Le spectateur choisit un nombre entier strictement positif
(b) Il le multiplie par 9
(c) Il forme récursivement la somme des chiffres de ce produit jusqu’à n’avoir qu’un
seul chiffre
(d) Il retranche 5 à ce résultat
(e) Il code le résultat final par une lettre selon la règle 1 ↔ A, 2 ↔ B, 3 ↔ C, etc.
Là-dessus le spectateur écrit sur un morceau de papier, sans le montrer au magicien,
le nom d’un pays européen commençant par cette lettre. Maintenant le magicien
triomphe en devinant le nom écrit sur le papier. Expliquer comment cela est possible.
page 26
App. des mathématiques, SAM
1ère année
2.10. Exercices
21) Calculer les restes des divisions par 37 de 1, 10, 100, 1′ 000, 10′ 000 et 100′ 000.
a) En déduire le reste de la division de 1085 par 37
b) Déterminer si le nombre 205′ 390′475′ 218 est divisible par 37.
22) Petit théorème de Fermat
Soit p un nombre premier.
Alors :
a) ap ≡ a (mod p) pour tout a ∈ Zp (ou, de manière équivalente, pour tout a ∈ Z).
b) ap−1 ≡ 1 (mod p) pour tout a ∈ Zp \ {0̇} (ou, de manière équivalente, avec a et p
premiers entre eux).
Montrer le petit théorème de Fermat.
Pour la première partie, effectuer une preuve par récurrence sur a ∈ Z.
23) Quel est le jour de la semaine des dates suivantes :
a) votre naissance.
b) votre vingtième anniversaire.
c) 20 août 1601, naissance de Pierre de Fermat.
d) 4 janvier 1643, naissance d’Isaac Newton.
e) 15 avril 1707, naissance de Leonhard Euler.
f) 14 novembre 1716, mort de Gottfried Wilhem von Leibnitz.
g) 27 septembre 1783, mort d’Etienne Bézout.
h) 23 février 1855, mort de Carl Friedrich Gauss.
i) 21 juillet 1969, premiers pas sur la Lune.
j) 23 juin 1974, plébiscite jurassien.
24) Toutes les publications en série, comme les journaux et les périodiques, sont identifiées
par un numéro ISSN (International Standard Serial Number). L’ISSN comporte huit
caractères répartis en deux groupes de quatre, ces groupes étant séparés par un tiret.
Par exemple, l’ISSN 1423 - 1778
est associé au titre ”Le Quotidien Jurassien”.
Les sept premiers caractères sont des chiffres qui caractérisent la publication. Le dernier caractère, situé en 8e position, sert de clé de contrôle et est pris dans la liste 0,
1, 2, 3, 4, 5, 6, 7, 8, 9, X (qui représente 10). Ce dernier chiffre dépend de ceux qui
précèdent. Ainsi, si le code ISSN est a1 a2 a3 a4 − a5 a6 a7 a8 , a8 est déterminé de manière
à ce que :
a8 ≡ 11 − 8a1 − 7a2 − 6a3 − 5a4 − 4a5 − 3a6 − 2a7
(mod 11)
a) Combien peut-on référencer de journaux ou de périodiques avec ce système ?
b) Calculer la clé de contrôle du numéro ISSN 1032 - 105 et celle du numéro ISSN
0358 - 210
c) Le troisième chiffre du numéro ISSN d’un journal est illisible. On le note a3 . Le
numéro se présente sous la forme ISSN 24a3 6 − 3014. Quel est le chiffre manquant
a3 ?
d) Montrer que si on permute deux chiffres juxtaposés (différents), la clé de contrôle
est modifiée et l’erreur est détectée.
Indication : calculer la différence des deux clés de contrôle.
page 27
1ère année
App. des mathématiques, SAM
2.11
2.11. Solutions des exercices
Solutions des exercices
1) a) 24
b) 3
c) 1
d) 2
3) (u; v) = (−21; 55)
4) a) oui
x
5) a)
y
x
c)
y
x
e)
y
x
g)
y
x
i)
y
b) oui
=
=
=
=
=
=
=
=
=
=
c) non
5 − 2k
−15 + 7k
−260 − 59k
−150 − 34k
−15 − 3k
−45 − 8k
41 − 85k
−27 + 56k
−1995 − 17k
1425 + 12k
x
y
x
d)
y
b)
= −26 − 34k
= 166 + 217k
= −6 − 8k
=
4 + 5k
f) S = ∅
h) S = ∅
j) S = ∅
7) a) 11 billets à 12 CHF et 9 billets à 17 CHF
b) Il y a eu une erreur dans l’encaissement des billets.
x = 24 + 5k
8) a)
b) S = ∅
y = 12 + 3k
9) a) 11121
b) 11112
c) 1621
d) 10210102
e) 110101111100
f) 33051
g) 12314
h) 37704
b) 6′ 025
10) a) 585
c) 1′ 865
d) 26′ 149
e) 23′ 889
f) 15′ 624
g) 51′ 604
h) 112′ 347
11) a) 1
b) 2
d) 4
e) 2
12) a) 9
b) 6
c) 4
c) 8
16) a) 1
c) 4 ou 6
17) b) 1) Z2 : 1̇
4) Z5 : 1̇, 2̇, 3̇, 4̇
2) Z3 : 1̇, 2̇
2) Z6 : 1̇, 5̇
c) 2̇
d) ∅
page 28
3) Z4 : 1̇, 3̇
1ère année
App. des mathématiques, SAM
2.11. Solutions des exercices
e) 2̇, 3̇, 4̇
18) a) S = ∅
b) S = {0̇; 2̇; 4̇}
21) a) Reste : 10
b) Reste : 30
23) c) lundi
d) dimanche
e) vendredi
f) samedi
g) mercredi
h) vendredi
i) lundi
j) dimanche
24) a) 107 références possibles
b) 1032 - 1051 et 0358 - 2108
c) a3 = 2
page 29