Régimes transitoires du premier ordre

Sup PCSI1 - Exercices de physique Régimes transitoires du premier ordre
1
Régimes transitoires du premier ordre
Un peu de méthode !
La procédure usuelle de résolution d’un exercice sur le régime transitoire peut se décomposer en trois phases :
1- Mise en équation du circuit, et mise sous forme canonique de la (des) équation(s) différentielle(s) ;
2- Résolution mathématique de l’ (des) équations différentielle(s) ;
3- Détermination des constantes d’intégration, à partir des conditions de continuités portant sur les
grandeurs du circuit, et des valeurs initiales de ces grandeurs.
La prise en compte de ces conditions initiales, associée aux considérations concernant les comportements des
composants en régime permanent (atteint au bout d’un temps « infini ») permet de prévoir sans calcul
différentiel l’allure des solutions, ou de valider a postériori les résultats obtenus par ce calcul.
La mise en équation, évidente dans le cas de circuits à une maille, peut demander parfois la combinaison entre
plusieurs équations (différentielles ou non). Il est parfois utile de dériver par rapport au temps une équation
différentielle (ainsi, les termes de charges deviennent des intensités).
La résolution mathématique des équations différentielles linéaires à coefficients constants est algorithmique.
Elle ne doit pas poser de difficultés.
Dans le cas le plus général (équations différentielles avec second membre), on aura : SEC = SGESSM + SPEC
La dernière phase, déterminant les constantes d’intégration à partir des conditions initiales portera sur la
solution de l’équation complète SEC (attention aux confusions avec SGESSM !).
Rappelons les conditions de continuité : l’intensité i(t) traversant une bobine est une fonction continue du
temps t ; la tension u(t) aux bornes d’un condensateur (ou la charge q(t) qu’il porte) est une fonction continue
du temps t. Les relations u = L.(di/dt) et i = C.(du/dt) permettent de tirer des conditions initiales sur les
valeurs des dérivées des fonctions i(t) ou u(t).
Exemple :
Supposons qu’à t = 0
_
: i = 0. On ferme K à t = 0.
En écrivant la loi de maille sur (E, R, L) à t = 0
+
, et tenant compte de i(0
+
) = i
L
(0_) = 0,
on tire E + u
R
(0) = u
L
(0) = u(0).
Ainsi L(di
L
/dt)(0) = u(0) = E donne accès à : (di
L
/dt)(0) = E/L.
1. Réponse d'un circuit R-C série à un échelon de tension :
A) Un dipôle R-C série est placé en série avec une source de tension
de f.e.m. E constante et de résistance interne r. Le condensateur est
initialement déchargé. A t = 0, on ferme l'interrupteur K.
a) Quel est le dipôle de Thévenin vu des bornes du condensateur C ?
b) Déterminer i (t) et tracer son graphe.
c) Exprimer les tensions u
c
(t), u
R
(t) et représenter leur graphe.
Préciser le temps caractéristique τ et la valeur finale u
c-rp
de u
c
(t).
B) L’observation expérimentale de u
c
(t) au moyen d’une carte
d’acquisition de résistance d’entrée R
e
revient à brancher cette
résistance en dérivation sur le dipôle R-C.
E
r
i
R
K
générateur
u
R
(t)
u
C
(t)
C
E
r
K
R
e
R
C
u
c
(t)
R
E
K u
i
L

Sup PCSI1 - Exercices de physique Régimes transitoires du premier ordre
2
0
1
2
3
0 0,01 0,02 0,03 0,04
u (V)
t(ms)
u(t)
-300
-200
-100
0
100
200
300
-0,15 -0,1 -0,05 0 0,05 0,1 0,15
di/dt (A/s)
intensité (A)
portrait de phase
Le condensateur étant initialement non chargé, on ferme K à t = 0. La résistance r est négligeable.
a) Etablir l’équation différentielle régissant u
c
(t).
b) Calculer u
c
(t). Quelles sont les modifications apportées par la présence de la carte d’acquisition ?
AN : E = 5,0 V ; R = 10 kΩ ; R
e
= 40 kΩ ; C = 1,0 µF.
R : A) en écrivant la loi des mailles et en dérivant / t :
( )
C
i
dt
di
Rr ++
= 0, car i = dq/dt
d’où i(t) =
( ) +
−
+CRr
t
rR
Eexp
. Puis u
c
(t) = E - ( R + r).i (t).
B)
RC
E
u
dt
du
CC
=+
'
τ
avec τ’ =
RR
CRR
e
e
+
le temps caractéristique et la valeur finale de u
C
seront modifiés.
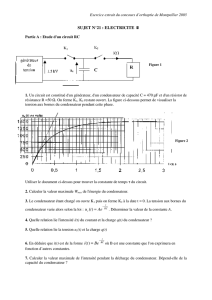
2. Exploitation d’un graphe :
On réalise la charge d’un condensateur à
travers un résistor de résistance R = 1,0 kΩ.
L’alimentation stabilisée utilisée est réglée à
une f.e.m. de 2,0 V, et a une résistance de
sortie de 5 Ω.
Déterminer le plus précisément possible la
capacité du condensateur à partir du graphe.
R : C = 9,0 nF.
3. Réponse d'un circuit inductif à un échelon de courant :
Un circuit inductif, constitué d'une résistance R' en parallèle avec une inductance L placée en série avec
une résistance R est soumis à un échelon de courant délivré par un générateur de courant idéal : I (t) = 0 pour t
≤ 0, et I (t) = I
o
= constante pour t > 0.
a) Déterminer l'intensité instantanée i (t) du courant traversant la bobine.
b) En déduire les expressions de i’(t), le courant traversant R', et u (t), la
tension aux bornes de la dérivation.
c) Tracer i (t) et u (t).
R : équation du circuit :
o
I
L
R
i
L
RR
dt
di '' =
+
+
4. Exploitation d’un portrait de phase.
Un générateur de basse fréquence (G.B.F.), de
résistance de sortie r
S
= 50 Ω, délivre une tension
créneau d’amplitude E = 6,0 V.
On branche ce générateur en série avec une
bobine d’inductance L et de résistance interne r.
La fréquence du G.B.F. est suffisamment basse
pour que le régime permanent soit pratiquement
atteint à chaque alternance.
Io
K
R'
R
L

Sup PCSI1 - Exercices de physique Régimes transitoires du premier ordre
3
A partir du portrait de phase fourni, déterminer les valeurs de l’intensité i(t) traversant la bobine et de sa
dérivée temporelle aux instants correspondant aux ruptures de régime du circuit.
Proposer une allure du signal i(t) sur deux périodes du G.B.F.
En s’appuyant sur l’équation différentielle du circuit, déduire du portrait de phase les valeurs de l’inductance L
et de la résistance interne r de la bobine.
R : r = 10 Ω et L = 60 mH.
5. Mouvement d’une particule avec frottement fluide :
Une particule de masse m est soumise à l'action de la pesanteur g. Elle subit durant son déplacement une
force de frottement de forme f = -kv, proportionnelle à sa vitesse. La trajectoire est supposée rectiligne.
Montrer que la vitesse de la particule va évoluer vers une vitesse limite. Au bout de combien de temps la
particule a-t-elle une vitesse égale à la moitié de sa vitesse limite ? à 99% de celle-ci ?
R : Par la R.F.D. dv/dt + (k/m)v(t) = g. Posons τ = m/k. ∆t
1/2
= τ.ln2 ;
∆t
99%
= τ.ln(100) ≈ 4,6.τ
6. Régime transitoire à deux phases d'un circuit R-C :
e1 = 10 V ; r1 = 20 Ω ; R = 80 Ω ; C = 11 µF
eo = 4,5 V ; ro = 10 Ω
On considère le circuit suivant :
On ferme l'interrupteur K en position "0" à l'instant t = 0, C étant
initialement déchargé. Puis, à l'instant t1 où la charge du
condensateur atteint la moitié de celle atteinte au bout d'un temps
infini, on commute K en position "1".
1) Calculer littéralement puis numériquement t1. On posera τ
o
= (r
o
+ R)C.
2) Ecrire la loi q (t) pour t ≤ t1 et t > t1. On posera τ
1
= (r
1
+ R)C
3) Représenter q(t) et i(t). Calculer l'instant t2 ≠ 0 où la charge q s'annule.
R : t
1
= τ
o
Ln2. q(t) = Ce
o
(1-exp(-t/ τ o)) ; q(t) = (Ce
1
+ Ce
o
/2) exp(-(t-t
1
)/ τ
1
)-Ce
1
. i = dq/dt.
7. Régime transitoire pour deux condensateurs en opposition :
On suppose qu'à l'instant initial t = 0 où l’on ferme l'interrupteur K, la charge
q1 du condensateur de la branche 1 vaut q
o
et que celle de l'autre
condensateur est nulle : q
2
= 0. On note i(t) l’intensité traversant
l’interrupteur, orientée de (2) vers (1). On pourra poser R= R
1
+ R
2
a) Montrer que les charges q
1
(t) et q
2
(t) sont liées par une relation faisant
intervenir q
o
. Prévoir sans calcul différentiel les valeurs initiale et finale de
l’intensité i(t). Déterminer q1(t), puis tracer l’allure des courbes solutions
q
1
(t), q
2
(t) et i(t). Commenter le comportement du circuit pour t tendant vers l'infini.
b) Déduire l’énergie W dissipée par effet Joule durant le processus à partir d’un bilan énergétique.
K
C
1
C
2
R
1
R
2
(1)
(2)
q
1
-q
1
-q
2
q
2
i(t) u
1
u
2
r
o
e
o
e
1
r
1
R C
K
1
0

Sup PCSI1 - Exercices de physique Régimes transitoires du premier ordre
4
R : a)
dt
dq
dt
dq
i
21
−== d’où q
1
+ q
2
= cste = q
o
. puis écrire la loi de maille et en tirer une équation en q
1
(t). La
résolution donne q
1
(t) . q
2
(t)= q
o
–q
1
(t) ; i(t) est la courbe dérivée de q
1
(t).
b)
( ) ²
2
1
²
2
1
)²(
21
01
∞
∞
+−==
∫
UCC
C
q
dttRiW
o
joule où U
∞
est la tension finale sur q
1
et q
2
.
8. Réponse à une tension en dent de scie :
On considère le circuit suivant :
A l'instant initial, les condensateurs C et C' sont déchargés.
On applique aux bornes d'entrée du circuit une tension variable Ve(t).
On appelle Vs(t) la tension de sortie, aux bornes de R ou C'.
1) Etablir l'équation différentielle reliant Vs(t), sa dérivée par rapport au
temps et la dérivée par rapport au temps de la tension d'entrée Ve(t).
2) La tension d'entrée est une impulsion de durée T décrite par :
pour t ≤ 0 : Ve(t) = 0 et t > T ; pour 0 < t ≤ T : Ve(t) = k.t
(où k est une constante).
Exprimer Vs(t) pour tout temps t et représenter les courbes Ve(t) et Vs(t) pour 0 < t < 2T.
On supposera T >> R.(C + C') = τ.
R : Par la loi de nœud :
dt
dV
CC
C
V
CCRdt
dV
e
s
s
')'(
1
+
=
+
+ ; V
s
(t) = kRC(1-exp(-t/ τ )) pour 0 < t < T et
V
s
(t)=kRC.exp(-(t-T)/ τ ) pour t > T.
9. Réponse d'un circuit RC à un générateur de courant :
1. On envisage le modèle suivant, où un générateur de courant de cém I
o
alimente,
à partir de t = 0, l'ensemble résistor et condensateur.
Calculer l'expression de la tension u(t) aux bornes du condensateur. Discuter de la
validité de ce modèle.
2. On prend en compte la conductance du générateur de courant selon le modèle dit « de Norton », en
considérant un résistor de résistance R
N
placé en dérivation sur la source de courant. On suppose R
N
grand
devant R. Expliciter maintenant q(t) en fonction de I
o
, R, C et R
N
.
A quelle condition sur t l'expression obtenue rejoint-elle le modèle précédent ?
R : 1. u(t) = I
o
.t /C, u(t) →∞ quand t →∞ .
2. u(t) = R
N
.I
o
(1 – exp(-t/ τ )) où τ = (R
N
+ R).C
faire un DL1 pour t << τ : on rappelle que exp(x) ≈ 1 + x pour x au voisinage de 0.
Ve(t)
Vs(t)
R
C
C'
Io
R
C
u(t)