ECN 6578 Module 4 : Temps Continu et des Options

ECN 6578 Module 4 : Temps Continu et des
Options
William McCausland
Départment de Sciences Économiques
Université de Montréal
13 novembre 2006
Une suite de processus en temps continu
◮
Un processus pk en temps discret (k ∈ {0, 1, . . .}):
p0 = 0,
où
pk = pk −1 + ǫk ,
(
∆
avec probabilité π
ǫk =
−∆ avec probabilité (1 − π)
et ∆ et π sont des paramètres.
◮
Une suite (n = 1, 2, . . .) des processus à temps continu
(t ∈ [0, T ]) :
pn (t) ≡ p⌊nt/T ⌋ = p⌊t/h⌋
t ∈ [0, T ]
où ⌊x⌋ est le plancher de x et h = T /n.
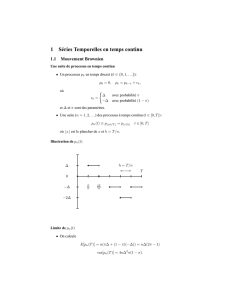
Illustration de pn (t)
h = T /n
∆
T
0
−∆
−2∆
T
n
2T
n
Limite de pn (t)
◮
On calcule
E [pn (T )] = n(π∆ + (1 − π)(−∆)) = n∆(2π − 1)
var[pn (T )] = 4n∆2 π(1 − π).
◮
Si on choisit ∆ et π en termes de n (ou h) afin que
◮
◮
E[pn (T )] = µT pour chaque n
var[pn (T )] = σ 2 T pour chaque n,
alors
1
π=
2
◮
√ !
µ h
1+
σ
√
∆ = σ h.
Avec ce choix de π(n) et ∆(n), p(t) = limn→∞ pn (t) est un
MB avec dérive µ et diffusion σ.
Propriétés des Mouvements Brownien
◮
3 propriétés de p(t):
1. Pour 0 ≤ t1 < t2 ≤ T
p(t2 ) − p(t1 ) ∼ N(µ(t2 − t1 ), σ 2 (t2 − t1 )).
2. Pour 0 ≤ t1 < t2 ≤ t3 < t4 ≤ T
p(t2 ) − p(t1 ) et p(t4 ) − p(t3 ) sont indépendants.
3. Tous les chemins échantillonaux (sample paths) sont
continus.
◮
Elles peuvent servir de la définition d’un MB.
◮
µ, σ et p(0) spécifie le processus.
◮
B(t) est un MB normalisé (ou standard): µ = 0, σ = 1.
Propriétés dérivés
◮
On peut dériver les propriétés suivantes à partir des
propriétés définitionnelles.
E [p(t2 )|p(t1 )] = p(t1 ) + µ(t2 − t1 )
var[p(t2 )|p(t1 )] = σ 2 (t2 − t1 )
cov[p(t1 ), p(t2 )|p(0) = 0] = σ 2 min(t1 , t2 ).
Le différentiel stochastique
◮
Le différentiel stochastique dB = B(t + dt) − B(t) a la loi
dB ∼ N(0, dt).
◮
Règles de multiplication :
dB dt = dt dB = (dt)2 = 0 dB dB = dt.
◮
Mouvement brownien p(t) avec drift µ et diffusion σ en
forme différentielle :
dp = dp(t) = µdt + σdB,
◮
Par exemple, calculer (dp)2 :
(dp)2 = (µdt + σdB)2
= µ2 (dt)2 + σ 2 (dB)2 + 2µ(dB)(dt)
= σ 2 dt.
Processus Itôs et la lemme d’Itô
◮
La classe des processus Itôs comprend le MB.
◮
Elle est fermé sous des transformations générales : si p
est un processus Itô, q = f (p, t) l’est aussi.
◮
La lemme de Itô donne l’EDS de f (p, t) à partir de celui de
p:
∂f
1 ∂2f
∂f
dp +
dt +
(dp)2
df =
∂p
∂t
2 ∂p 2
Exemple
◮
Trouver l’EDS de P(t) = ep(t) où dp = µdt + σdB(t) :
f (p, t) = ep
∂f
= ep
∂p
∂2f
= ep
∂p 2
∂f
=0
∂t
1
dP = ep dp + 0 + ep (dp)2
2
1
= P(µdt + σdB) + P(σ 2 dt)
2
1 2
= (µ + σ )P dt + σ P dB
2
◮
On appèle p un MB arithmétique; P, un MB géométrique.
◮
Trouver les dynamiques d’une fonction non-linéaire d’un
processus en temps discret est désespéré : un avantage
rélatif du temps continu.
Options
◮
Une option est un contrat entre un émetteur et un
détenteur concernant un actif sous-jacent.
◮
Une option d’achat (call option) donne l’option (pas
l’obligation) au détenteur d’acheter l’actif.
◮
Une option de vente (put option) donne l’option de vendre
l’actif.
◮
Une partie du contrat est le prix d’exercise (strike price) X ,
le prix auquel l’achat ou la vente a lieu.
◮
Une autre partie du contrat est la date d’échéance
(expiration date) T .
◮
L’option peut être européenne, auquel cas le détenteur a
l’option seulement à T ; ou américaine, auquel cas le
détenteur a l’option jusqu’à T .
Hypothèses Black Scholes
◮
On va calculer le prix G(t) de une option d’achat
européene à partir du prix P(t) de l’actif sous-jacent, sous
les hypothèses suivantes très fortes.
◮
◮
L’échange en temps continu, pas de friction (taxe, coût de
transaction, contraint).
P(t) est un MB géométrique :
dP = µPdt + σPdB
◮
Il y a un rendement constant r sans risque à prix D(t) :
dD = Drdt
◮
Pas d’arbitrage.
Dérivation du formule Black Scholes pour G(t)
◮
La lemme d’Itô avec G(t) = G(P(t), t) donne (9.2.4 est
fausse)
∂G
∂G
1 ∂2G
(dP)2
dP +
dt +
∂P
∂t
2 ∂P 2
∂G
∂G
σ2 ∂ 2 G
=
[µPdt + σPdB] +
dt + P 2
dt
∂P
∂t
2
∂P 2
∂G
∂G ∂G σ 2 2 ∂ 2 G
dt + σP
= µP
+
+ P
dB
∂P
∂t
2
∂P
∂P 2
≡ Gµg dt + Gσg dB,
dG =
où
∂G ∂G σ 2 2 ∂ 2 G
1
+
+ P
µP
,
µg ≡
G
∂P
∂t
2
∂P 2
1
∂G
σg ≡
σP
.
G
∂P
Un portefeuille autofinanceant
◮
On a les portefeuilles (Ip (t), Ig (t), Id (t)), où Ip (t) est la
somme en dollars investie en l’actif sous-jacent, etc.
◮
On suppose que le portefeuille est autofinanceant :
Ip (t) + Id (t) + Ig (t) = 0.
◮
Si dI(t) est le rendement en dollars à ce portefeuille,
dI =
◮
Ig
Ip
I
dP + d dD + dG.
P
D
G
Substituer dD, dP, dG et éliminer Id (t) par
autofinancement:
dI = [(µ − r )Ip + (µg − r )Ig ]dt + [σIp + σg Ig ]dB
Un portefeuille autofinanceant sans risque
◮
On rend dI non-aléatoire avec Ip = Ip∗ et Ig = Ig∗ tel que
σIp∗ + σg Ig∗ = 0 ∀t ∈ [0, T ].
◮
◮
Le portefeuille (Ip∗ , Ig∗ , −Ip∗ − Ig∗ ) est autofinanceant et sans
risque.
Par l’absence d’arbitrage, dI ≡ 0, et donc
(µ − r )Ip∗ (t) + (µg (t) − r )Ig∗ (t) = 0,
et
Ip∗
σg
P ∂G
=−
=
.
∗
Ig
σ
G ∂P
Une équation différentielle partielle
◮
Ça donne l’équation différentielle partielle
∂G ∂G
σ2 2 ∂ 2 G
+ rP
P
+
− rG = 0.
2
2
∂P
∂t
∂P
◮
Deux conditions limites:
G(P(T ), T ) = max[P(T ) − X , 0]
G(0, t) = 0
La formule Black Scholes
◮
La solution unique est la formule célèbre BS:
G(P(t), t) = P(t)Φ(d1 ) − Xe−r (T −t) Φ(d2 ),
où
d1 ≡
d2 ≡
log[P(t)/Xe−r (T −t) ] + 21 σ 2 (T − t)
√
,
σ T −t
log[P(t)/Xe−r (T −t) ] − 21 σ 2 (T − t)
√
.
σ T −t
Couverture Parfaite
◮
La relation
donne
Ip∗
σg
P ∂G
=
.
=−
∗
Ig
σ
G ∂P
np∗ (t)
∂G(t)
=−
∗
ng (t)
∂P
où np∗ ≡ Ip∗ /P, le nombre de l’actif tenu à t, ng∗ ≡ Ig∗ /G.
◮
Ce ratio est le rapport de couverture (hedge ratio).
◮
On fait les adjustements du portefeuille continuement afin
que le portefeuille reste sans risque : “couverture parfaite”
(perfect hedging).
◮
On ne peut le faire en temps discret.
Les Grecs
◮
Sensibilités suivantes des options sont utile pour les
praticiens:
∆≡
∂G
∂P
∂2G
∂P 2
Θ≡
∂G
∂t
∂G
∂G
V (Vega) ≡
∂r
∂σ
Avec la formule BS, on peut évaluer ces expression en
forme réduite.
R (Rho) ≡
◮
Γ≡
L’approche martingale
◮
L’approche qui nous a donné la formule Black-Scholes:
◮
◮
◮
Trouver un portefeuille dynamique, autofinanceant, sans
risque.
Imposer la condition de l’absence de l’arbitrage.
Résoudre l’équation partielle différentielle qu’on obtient
avec des conditions limites impliqué par les termes du
contrat.
ne dépend pas des détails des préférences, mais
seulement de l’absence de l’arbitrage.
◮
Donc, la formule tient pour toute préférence qui ne permet
pas de l’arbitrage.
◮
En particulier, une formule qui tient pour des agents
risque-neutres tient pour toute préférence sans arbitrage.
Valorisation risque-neutre
◮
Dans un monde risque-neutre, tout les actifs doivent avoir
le même rendement espéré:
µ=r
G(t) = e−r (T −t) Et [max(P ∗ (T ) − X , 0)],
où P ∗ (t) est la modification de P(t) pour tenir compte de la
risque-neutralité :
dP ∗ = rP ∗ dt + σP ∗ dB.
P ∗ (T ) est log-normal avec
E [log P ∗ (T )|P(t)] = log P(t) + (r − σ 2 /2)(T − t),
var[log P ∗ (T )|P(t)] = σ 2 (T − t).
Estimation par maximimum de vraisemblance
◮
Supposons qu’on a un processus P(t):
dP(t) = a(P, t; α)dt + b(P, t; β)dB(t)
◮
◮
t ∈ [0, T ]
où a est la (fonction de) derive, b est la diffusion et
θ = (α, β) le paramètre à estimer.
On n’observe pas P en temps continue, mais plutôt les
valeurs P0 , P1 , . . . , Pn au moments t0 < t1 < . . . < tn (pas
necessairement uniforme).
La densité conjointe des prix est (P(t) est Markov)
f (P0 , . . . , Pn ; θ) = f0 (P0 ; θ)
n
Y
k =1
f (Pk ; tk |Pk −1 ; tk −1 , θ) =
et la log-vraisemblance est
L(θ) =
n
X
k =0
log fk
n
Y
k =1
fk
Computation des fk
◮
On obtient les fk à partir de P. fk , une fonction de Pk et tk ,
est la solution de l’équation partielle différentielle
Fokker-Planck :
∂fk
∂(afk ) 1 ∂ 2 (b 2 fk )
=−
+
,
∂t
∂P
2 ∂P 2
avec la condition initiale
fk (P, tk −1 |Pk −1 , tk −1 ) = δ(P − Pk −1 ),
où δ(x) met une masse unitaire de probabilité à zéro.
◮
Avec les fk en terms de θ, on calcule
θ̂ = argmaxθ∈Θ L(θ).
Résultats
◮
Sous les conditions de régularité (y compris la stationarité),
p
θ̂ → θ
et
où
√
a
n(θ̂ − θ) ∼ N(0, I −1 (θ)),
1 ∂ 2 L(θ)
I(θ) = −E
n ∂θ∂θ ′
On peut estimer I(θ) comme
Î = −
◮
1 ∂ 2 L(θ̂)
.
n ∂θ∂θ ′
Sous les conditions de régularité, θ̂ est asymptotiquement
efficace dans la classe des estimateurs convergents et
asymptotiquement normaux.
Estimation d’autres quantités
◮
Si on a une formule G(P, t) pour le prix d’un option, le MLE
du prix est:
Ĝ = G(P(t; θ̂), t).
◮
Une approximation linéaire de G près de θ̂ (la méthode
Delta) donne sa variance approximative :
√
a
n(Ĝ − G) ∼ N(0, V (θ)),
où
V (θ) ≡
◮
∂G
∂θ
′
I
−1
(θ)
∂G
∂θ
.
On estime V (θ) par V (θ̂). On peut estimer les MLE est les
variances des grecs ∆, Γ, Θ, R et V de façon semblable.
Exemple : Mouvement Brownien I
◮
Pour le mouvement Brownien géométrique,
dP = µPdt + σPdB.
◮
◮
{Pk } n’est pas stationnaire, mais rk ≡ log(Pk /Pk −1 ) l’est.
Par la lemme d’Itô,
d log P = (µ − σ 2 /2)dt + σdB ≡ αdt + σdB.
◮
Les log-rendements rk (h) sont i.i.d. normal:
rk (h) = log(Pk /Pk −1 ) = log(Pk ) − log(Pk −1 ) ∼ N(αh, σ 2 h).
Exemple : Mouvement Brownien I
◮
La log-vraisemblance est
n
X
n
(rk (h) − αh)2
L(α, σ) = − log(2πσ 2 h) − (2σ 2 h)−1
2
k =1
et les MLE sont
n
α̂ =
1 X
rk (h)
nh
k =1
n
σ̂ 2 =
1 X
(rk (h) − α̂h)2 .
nh
k =1
Valorisation des options par simulation Monte Carlo I
◮
Souvent, les termes d’une option dépend pas seulement
du prix de l’actif sous-jacent à T, mais aussi du chemin
dans la période [0, T ].
◮
Une option “look-back” donne le droit de vendre une unitée
de l’actif sous-jacent en T au prix d’exercise
max P(t).
t∈[0,T ]
◮
Par la méthode martingale pour la valorisation des options,
la valeur initiale (t = 0) est
H(0) = e−rT E ∗ [ max P(t) − P(T )]
t∈[0,T ]
= e
−rT
∗
E [ max P(t)] − P(0)
t∈[0,T ]
où l’espérance E ∗ est par rapport à la loi risque neutre.
Valorisation des options par simulation Monte Carlo II
◮
Pour i = 1, . . . , m
◮
Pour j = 1, . . . , n
◮
◮
◮
Tirer P (m) (ih)|P (m) ((i − 1)h) selon la loi martingale, où
h = T /n.
H (m) = e−rT maxj∈{1,...,n} P(jh) − P(0)
Ĥ(0) =
1
m
Pm
i=1 H
(m)
Approximation des processus en temps continue I
◮
Soit P un processus en temps continu (P(0) donné) :
µ(P) dt + σ(P) dB
◮
Processus approximative Pδ constant sur [0, δ), [δ, 2δ), etc :
Pδ (t) = Pδ (δ⌊t/δ⌋)
◮
On cherche des approximations à la loi P(t)|P(0) afin de
◮
◮
◮
estimer les paramètres des fonctions µ, σ 2
faire des prévisions
évaluer les prix des options
Discretisation Euler
◮
Définition de Pδ pour la discretisation Euler :
Pδ (n) − Pδ (n − 1) = µ(Pδ (n − 1)) + σ(Pδ (n − 1))δ1/2 ǫn
ǫn ∼ N(0, 1)
◮
La loi Pδ (t)|P(0) converge à la loi P(t)|P(0) avec δ → 0.
Arbre Binomial
◮
Définition de Pδ pour l’arbre binomial :
Pδ (n) − Pδ (n − 1) = ǫn ,
où
(
uδ (Pδ (n − 1)) avec probabilité pδ (Pδ (n − 1))
ǫn =
dδ (Pδ (n − 1)) avec probabilité 1 − pδ (Pδ (n − 1))
◮
On obtient uδ , dδ et pδ avec les équations
1
E[(Pδ (n) − Pδ (n − 1))|Pδ (n − 1)] = µ(Pδ (n − 1))
δ
◮
1
var[(Pδ (n) − Pδ (n − 1))|Pδ (n − 1)] = σ 2 (Pδ (n − 1))
δ
1
E[(Pδ (n) − Pδ (n − 1))3 |Pδ (n − 1)] = 0.
δ
La loi Pδ (t)|P(0) converge à la loi P(t)|P(0) avec δ → 0.
Arbre binomial et la valorization des options
◮
Supposez que le prix Pn ≡ P(nδ) d’un actif suit le
processus suivant :
u(Pn ) = uPn
◮
d (Pn ) = dPn
p(Pn ) = p.
Autrement dit,
Pn+1
(
Pn (1 + u) avec probabilité p
=
Pn (1 + d ) avec probabilité (1 − p).
◮
Autrement dit, Pn+1 = Pn [1 + uǫn + d (1 − ǫn )], où ǫn et
Bernoulli avec probabilité p.
◮
C’est l’arbre binomial pour un mouvement brownien
géométrique.
Implications de l’absense d’arbitrage I
◮
Supposez qu’il existe un actif sans risque avec rendement
net r par période de durée δ.
◮
Absence d’arbitrage entraine d < r < u.
◮
Soit {n; ǫ01 , . . . , ǫ0n } l’actif Arrow Debreu qui paie un dollar à
n si ǫ1 = ǫ01 , ǫ2 = ǫ02 , etc.
◮
Soit C(n; ǫ01 , . . . , ǫ0n ) son prix à 0.
◮
À t = 0, il y a deux actifs pour l’horizon t = 1 : l’actif avec
risque et l’actif sans risque.
◮
Il y a aussi deux états à t = 1, alors le marché est complet.
Implications de l’absense d’arbitrage II
◮
Calculons le prix de l’actif A-D {1; 1}, qui paie un dollar si
le prix de l’actif risqué augmente.
◮
Soit un portefeuille avec α unitées de l’actif sans risque et
β unitées de l’actif risqué.
◮
Si le portefeuille donne les même paiements que {1; 1},
α(1 + r ) + βP0 (1 + u) = 1
α(1 + r ) + βP0 (1 + d ) = 0.
◮
La solution unique est
α=
−1 1 + d
u−d 1+r
β=
1 1
u − d P0
Implications de l’absense d’arbitrage III
◮
Sans abritrage, le prix de {1; 1} est
C(1; 1) = α + βP0 =
◮
Même démarche pour {1; 0} donne
C(1; 0) =
◮
1 u−r
.
1+r u−d
Si on défine π = (r − d )/(u − d ) on obtient
C(1; 1) =
◮
1 r −d
1+r u−d
1
π
1+r
C(1; 0) =
1
(1 − π)
1+r
Notez que d < r < u entraine π > 0 et 1 − π > 0.
Probabilité risque neutre
◮
π est la probabilité risque neutre (ou probabilité de
valorisation ou probabilité martingale)
◮
π n’est pas la même chose que p, la vraie probabilité (ou
probabilité historique ou probabilité physique)
◮
Notez que
1
1
Eπ [P1 ] =
[πP0 (1 + u) + (1 − π)P0 (1 + d )] = P0
1+r
1+r
1
Eπ [1 + r ] = 1
1+r
◮
Conclusion : Les prix sont des paiements espérés selon la
probabilité risque neutre.
◮
Attention : Les agents ne sont pas nécessairement risque
neutre, est la probabilité risque neutre n’égal pas la
probabilité physique.
Plusieurs périodes
◮
◮
Valorisons l’actif A-D {2; 1, 0}.
Si ǫ1 = 1, il faut pouvoir acheter à t un actif A-D {1; 0}.
1
1+r (1
− π).
◮
On sait déjà que son prix est C(1; 0) =
◮
Pour avoir C(1; 0) dollars à t = 1 si ǫ1 = 1, il faut acheter
une quantité C(1; 0) de l’actif {1; 1} à t = 0.
◮
Son prix est C(2; 1, 0) = C(1; 1)C(1; 0) =
◮
En générale,
C(n; ǫ1 , . . . , ǫn ) =
n
Y
j=1
C(1; ǫj ) =
1
π(1
(1+r )2
− π).
1
π Hn (1 − π)n−Hn .
(1 + r )n
où Hn est le nombre de sauts (ǫj = 1) pour j = 1, . . . , n.
Valorisation des actifs composés
◮
Considerons un actif qui paie gn (ǫ1 , . . . , ǫn ) à t = n.
◮
Absense d’arbitrage entraine
C(gn ) =
1
X
ǫ1 =0
=
...
1
X
gn (ǫ1 , . . . , ǫn )C(n; ǫ1 , . . . , ǫn )
ǫn =0
1
1
X
X
1
.
.
.
gn (ǫ1 , . . . , ǫn )π Hn (1 − π)n−Hn
(1 + r )n
ǫ1 =0
=
◮
ǫn =0
1
Eπ [gn ].
(1 + r )n
On peut montrer que Sm = (1+r1)n−m Eπ [Sn |Sm ] pour m < n,
où Sn est le prix de n’importe quel actif. C’est la propriété
martingale.
Exemple de la valorisation des options
◮
Exemple : option d’achat européene, date d’exercise 2,
prix d’exercise K .
◮
Mettons que P0 (1 + d )2 < K < P0 (1 + d )(1 + u).
C’est le portefeuille suivant des actifs A-D :
◮
◮
◮
◮
◮
(1 + u)2 P0 − K unitées de {2; 1, 1),
(1 + u)(1 + d)P0 − K unitées de {2; 1, 0),
(1 + d)(1 + u)P0 − K unitées de {2; 0, 1).
Le prix de l’option est alors
π 2 [(1 + u)2 P0 − K ] + 2π(1 − π)[(1 + u)(1 + d )P0 − K ]
Marchés incomplets
◮
Considérons le modèle suivant de volatilité stochastique :
dPt = µ Pt dt + σt Pt dBtP
d log σt = a0 (a1 − log σt )dt + b dBtσ
◮
Il y a trois chocs maintenant (dt, dBtP et dBtσ ) au lieu de
deux (dt, dB) mais toujours deux actifs (l’actif sans risque
et l’actif sous-jacent).
◮
Le marché n’est pas complet, et l’option sur Pt n’est pas
rédondante.
◮
Il y a plusieurs probabilités risque neutre cohérentes avec
le processus Pt et l’absence d’arbitrage.
◮
On peut spécifier le prix d’une option sur un actif avec
volatilité stochastique en termes de r , la loi de Pt et la loi
d’un processus qui donne la prime de volatilité (qui est un
degré de liberté).