05 Parallèles. Perpendiculaires 6èC

CH V Parallèles et perpendiculaires
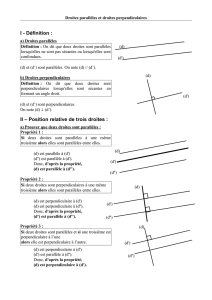
1. Droites perpendiculaires
A) Je trace trois droites perpendiculaires à la droite d
∆
1 ⊥ d
∆2 ⊥ d ∆ : lire delta ( lettre grecque )
∆
3 ⊥ d
Il existe une infinité de droites perpendiculaires à la droite d.
B) Je retiens
SI deux droites sont perpendiculaires à une même troisième droite
ALORS ces deux droites sont parallèles.
Cette phrase construite avec SI . . . ALORS . . . est appelée un théorème.
Dans un exercice, elle permet d'expliquer que deux droites sont parallèles.
SI je sais que ALORS je suis sûr que ∆ 1 // ∆ 2
Lorsqu'on explique, on dit qu'on démontre et les explications forment la démonstration.
!
2. Droites parallèles
A) Je trace UNE droite parallèle à une droite d ( avec règle et équerre )
Propriété : Il existe une infinité de droites parallèles à une droite d.
∆1∆2∆3
d
∆ 1 ⊥ d
∆ 2 ⊥ d
∆
d
1. Placer l’équerre le long de la droi# d.
2. Placer la règle le long de l’équerre.
3. Bien #nir la règle. Faire glisser l’équerre le long de la règle
4. Tracer la droi# para&èle le long de l’équerre

B) Je trace deux droites parallèles à une droite d
∆ 1 // d
!!!!!!!!!!∆
2 // d
Théorème 2
SI deux droites sont parallèles à une même troisième droite
ALORS ces deux droites sont parallèles entre elles.
C) Je trace une droite perpendiculaire à deux droites parallèles
Théorème 3
SI deux droites sont parallèles et SI une droite ∆ est perpendiculaire à l’une des parallèles
ALORS cette droite ∆ est perpendiculaire à l’autre parallèle.
3. Droites non parallèles
A) Droites sécantes
Deux droites qui ne sont pas parallèles
sont appelées droites sécantes.
Leur unique point de rencontre s’appelle leur point d’intersection.
On dit que les droites d et d ‘ sont sécantes en O
B) Droites concourantes
Plusieurs droites ( plus de deux ) qui passent par un même point
sont appelées droites concourantes.
On dit que les droites d1, d2, et d3 sont concourantes en O.
∆1
∆2
d
∆1
∆2
∆
O
d1
d3
d2
d
d ’
O

4. Trapèze
A) Définition
Un trapèze est un quadrilatère qui a deux côtés et deux seulement parallèles.
A
DC
B
[AB] // [CD]
B) Vocabulaire
Les deux côtés parallèles s’appellent les bases.
[AB] est la petite base et [DC] est la grande base.
5. Parallélogramme
A) Définition
Un parallélogramme est un quadrilatère qui a ses côtés parallèles 2 à 2.
A
DC
B
[AB] // [DC]
[AD] // [BC]
B) Notation
8 noms sont possibles pour ce parallélogramme :
ABCD BCDA CDAB DABC
ADCB BADC CBAD DCBA
6. Rectangle
A) Définition
Un rectangle est un parallélogramme qui a un angle droit
[AB] // [DC]
[AD] // [BC]
et
DAB
∑
= 90°
A
DC
B
B) Remarque
Si 1 angle est droit alors tous les autres angles du parallélogramme sont droits.
Explication sur le cahier d'exercices.

7. Losange
A) Définition
Un losange est un parallélogramme qui a deux côtés consécutifs égaux.
( côtés consécutifs = côtés qui se suivent )
[AB] // [DC]
[AD] // [BC]
et
AB = BC
//
//
A
D
C
B
B) Remarque
Si 2 côtés consécutifs sont égaux alors les 4 côtés sont égaux.
8. Carré
A) Définition
Un carré est parallélogramme qui a un angle droit et 2 côtés consécutifs égaux.
( c’est à la fois un rectangle et un losange )
[AB] // [DC]
[AD] // [BC]
AB = BC et
DAB
∑
= 90°
//
A
DC
B
//
B) Propriété
Tous les côtés sont égaux. Tous les angles sont droits.