Figures géométriques

Figures géométriques
I) Les triangles
1°) Triangles quelconques
ABC est un triangle; A, B et C sont les sommets; [AB], [BC] et [AC] sont les côtés.
2°) Triangles particuliers
DEF est un triangle isocèle
: il a 2 côtés
égaux GHI est un triangle équilatéral: il a 3 côtés égaux
JKL est un triangle rectangle en L: il
a 1 angle droit :
Ç
L ; le côté opposé à
l’angle droit s’appelle hypoténuse MNO est rectangle isocèle

II) Les quadrilatères
1°) Définition
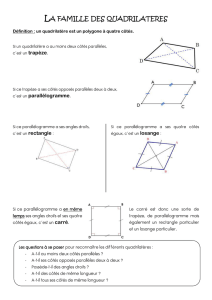
Un quadrilatère est une figure géométrique à 4 côtés.
2°) Quadrilatères particuliers
a) Le trapèze et cerf-volant:
• le trapèze est un quadrilatère ayant deux côtés
parallèles; par exemple (AB) // (DC)
On distingue des trapèzes particuliers:
trapèze isocèle trapèze rectangle
• le cerf-volant: MN = MP et NO= OP
On peut le construire à partir de deux triangles isocèles:
b) Le parallélogramme:
"Un parallélogramme est un quadrilatère dont
les côtés sont deux à deux parallèles"

Propriétés:
- Les côtés opposés d'un parallélogramme sont
égaux et parallèles
- Les diagonales d'un parallélogramme se coupent
en leur milieu
- Les angles opposés d'un parallélogramme sont
égaux.
Ceci permet de construire facilement un parallélogramme
au compas:
On prend un écartement de compas égal à AD et on place la pointe sur B: 1er arc de cercle.
On prend un écartement de compas égal à AB et on place la pointe sur D: 2ème arc de cercle.
A l'intersection de ces arcs de cercle, on trouve le point C tel que ABCD soit un parrallélogramme.
c) Le rectangle
Définition: "Un rectangle est un quadrilatère ayant 4 angles
droits"
Propriétés:
- Les côtés opposés d'un rectangle sont égaux et parallèles
- Les diagonales d'un rectangle sont égales et se coupent en
leur milieu
Remarque: un rectangle est inscriptible dans un cercle de centre
l'intersection de ses diagonales.
d) Le losange
Définition: "Un losange est un quadrilatère ayant ses quatre
côtés égaux"

Propriétés:
- "Les côtés d'un losange sont tous égaux et sont parallèles
deux à deux".
- "Les diagonales d'un losange sont perpendiculaires et se
coupent en leur milieu"
e) Le carré
Définition: Un carré est un parallélogramme ayant quatre
angles droits et quatre côtés égaux.
Propriétés:
- "Les côtés d'un carré
sont tous égaux et
parallèles deux à deux"
- "Les diagonales d'un carré sont égales,
perpendiculaires et se coupent en leur milieu"
Remarque: un carré est inscriptible dans un cercle de centre
l'intersection de ses diagonales
© J-P Diérick, professeur certifié de Mathématiques, collège du Triolo.