Diaporama sur la dérivation

Activité d’introduction
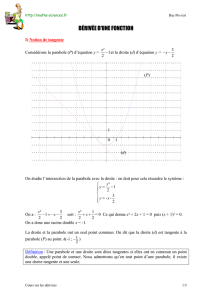
Nombre dérivé et tangente
Fonctions dérivées
[ Dérivation \
Partie 1
Lycée du golfe de Saint Tropez
Année 2015/2016
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
1 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
1
Activité d’introduction
2
Nombre dérivé et tangente
Nombre dérivé
Tangente à une courbe
3
Fonctions dérivées
Fonction dérivée
Dérivées des fonctions usuelles
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
2 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
I) Activité d’introduction
On s’intéresse à la courbe C f de la fonction f définie sur R par
f (x) = −x3 + 2x + 1
au voisinage du point A d’abscisse 1. Quel est l’ordonnée de A?
COURBE tangente_intro.ggb
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
3 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
I) Activité d’introduction
Cf
3
A
2
+
1
−3
−2
1
−1
2
−1
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
3 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
I) Activité d’introduction
On a agrandi le graphique 100 fois:
Cf
+
A
La courbe C f est très proche d’une droite D.
Quel est son coefficient directeur?
Quelle est son équation?
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
3 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
I) Activité d’introduction
Cf
3
A
2
+
1
D
−3
−2
1
−1
2
−1
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
3 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Coefficient directeur de la tangente
Coefficient directeur de D : −1
Coefficient directeur de (AM):
2
f (1 + h) − f (1)
h
A
+
M
+
1
Cf
D
+
−1
Première S ( Lycée du golfe de Saint Tropez)
+
11 + h
Dérivation
2
3
Année 2015/2016
4 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Coefficient directeur de la tangente
Coefficient directeur de D : −1
Coefficient directeur de (AM):
2
f (1 + h) − f (1)
h
A
+
M
+
1
C f approche de 0, la droite (AM) est approche de la tangente D.
Lorsque h est
D
Le coefficient directeur de la tangente est la «limite» du taux d’accroissement
+
−1
Première S ( Lycée du golfe de Saint Tropez)
+
11 + h
Dérivation
2
f (1 + h) − f (1)
.
h
3
Année 2015/2016
4 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Nombre dérivé
Tangente à une courbe
II) Nombre dérivé et tangente
a) Nombre dérivé
f étant une fonction définie sur un intervalle I, et a un réel appartenant à I
Définition
Le quotient
a + h.
f (a + h) − f (a)
s’appelle le taux de variation de la fonction f entre a et
h
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
5 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Nombre dérivé
Tangente à une courbe
II) Nombre dérivé et tangente
a) Nombre dérivé
f étant une fonction définie sur un intervalle I, et a un réel appartenant à I
Définition
Le quotient
a + h.
f (a + h) − f (a)
s’appelle le taux de variation de la fonction f entre a et
h
Définition
Dire que f est dérivable en a, c’est dire que lorsque h tend vers 0, le taux de
f (a + h) − f (a)
variation tend vers un réel ℓ, ce que l’on note lim
= ℓ.
h→0
h
Le réel ℓ se nomme le nombre dérivé de f en a et se note f ′ (a).
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
5 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Nombre dérivé
Tangente à une courbe
II) Nombre dérivé et tangente
a) Nombre dérivé
Définition
Dire que f est dérivable en a, c’est dire que lorsque h tend vers 0, le taux de
f (a + h) − f (a)
variation tend vers un réel ℓ, ce que l’on note lim
= ℓ.
h→0
h
Le réel ℓ se nomme le nombre dérivé de f en a et se note f ′ (a).
On considère la fonction f définie sur R par f (x) = x2 + 3.
Calculer f ′ (1) et contrôler avec votre calculatrice.
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
5 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Nombre dérivé
Tangente à une courbe
II) Nombre dérivé et tangente
a) Nombre dérivé
Définition
Dire que f est dérivable en a, c’est dire que lorsque h tend vers 0, le taux de
f (a + h) − f (a)
variation tend vers un réel ℓ, ce que l’on note lim
= ℓ.
h→0
h
Le réel ℓ se nomme le nombre dérivé de f en a et se note f ′ (a).
On considère la fonction f définie sur R par f (x) = x2 + 3.
Calculer f ′ (1) et contrôler avec votre calculatrice.
Calculatrice voir dans le livre p 83
Sur TI 83: math nbreDérivé ( nbreDérivé(X2 +3,X,1) )
Sur Casio dans OPTN choisir CALC puis d/dx
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
5 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Nombre dérivé
Tangente à une courbe
b) Tangente à une courbe
f étant une fonction définie sur un intervalle I et dérivable en a, a étant un réel
appartenant à I.
Définition
¡
¢
La¡tangente à une¢ courbe au point A a ; f (a) est la position limite des droites
M a + h ; f (a + h) lorsque h tend vers 0.
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
6 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Nombre dérivé
Tangente à une courbe
b) Tangente à une courbe
f étant une fonction définie sur un intervalle I et dérivable en a, a étant un réel
appartenant à I.
Définition
¡
¢
La¡tangente à une¢ courbe au point A a ; f (a) est la position limite des droites
M a + h ; f (a + h) lorsque h tend vers 0.
Propriétés
Le coefficient directeur de la tangente à la courbe C f au point d’abscisse a est
le nombre dérivé f ′ (a);
La tangente à la courbe C f au point d’abscisse a a pour équation :
y = f ′ (a)(x − a) + f (a)
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
6 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Nombre dérivé
Tangente à une courbe
Exemples
Faire les exercices 1, 2 et 3 page
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
7 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Fonction dérivée
Dérivées des fonctions usuelles
III) Fonctions dérivées
a) Fonction dérivée
Définition
f est une fonction définie sur un intervalle I.
On dit que f est dérivable sur I si f est dérivable en tout réel x de I.
Alors la fonction qui a x de I associe le nombre dérivé f ′ (x) s’appelle la fonction
dérivée de f et se note f ′ .
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
8 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Fonction dérivée
Dérivées des fonctions usuelles
b) Dérivées des fonctions usuelles
Théorème 1
Toute fonction affine f définie par f (x) = m x + p est dérivable sur R.
Sa fonction dérivée est définie sur R par f ′ (x) = m.
Démonstration:
Méthode
On calcule le taux d’accroissement
lorsque h tend vers 0.
Première S ( Lycée du golfe de Saint Tropez)
f (a + h) − f (a)
puis on détermine sa limite
h
Dérivation
Année 2015/2016
9 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Fonction dérivée
Dérivées des fonctions usuelles
Démonstration
Quels que soient les réels a et h, h 6= 0
f (a + h) − f (a) m(a + h) + p − (m a + b) m h
=
=
=m
h
h
h
donc le taux d’accroissement lorsque h tend vers 0 a pour limite m.
On a donc prouvé que quelque soit le nombre a, la fonction est dérivable en a et
f ′ (a) = m. Cela montre bien que la fonction dérivée est définie par f ′ (x) = m.
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
10 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Fonction dérivée
Dérivées des fonctions usuelles
Théorème 2
Toute fonction polynôme du second degré définie par f (x) = a x2 + b x + c est
dérivable sur R.
Sa fonction dérivée est définie sur R par f ′ (x) = 2a x + b.
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
11 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Fonction dérivée
Dérivées des fonctions usuelles
Démonstration
Quels que soient les réels α et h, h 6= 0
f (α + h) − f (α) a(α + h)2 + b(α + h) + c − (a α2 + b α + c)
=
h
h
a(α2 + 2α h + h2 ) + b(α + h) + c − (a α2 + b α + c)
=
h
a α2 + 2a α h + a h2 + b α + b h + c − a α2 − b α − c
=
h
2a α h + a h2 + b h
=
h
= 2a α + b + a h
donc le taux d’accroissement lorsque h tend vers 0 a pour limite 2a α + b.
On a donc prouvé que quelque soit le nombre α, la fonction est dérivable en α et
f ′ (α) = 2a α + b. Cela montre bien que la fonction dérivée est définie par
f ′ (x) = 2a x + b.
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
12 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Fonction dérivée
Dérivées des fonctions usuelles
Théorème 3
1
est dérivable sur R∗ .
x
1
Sa fonction dérivée est définie sur R∗ par f ′ (x) = − 2 .
x
La fonction inverse définie sur R∗ par f (x) =
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
13 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Fonction dérivée
Dérivées des fonctions usuelles
Démonstration
Quels que soient les réels α et h, α 6= 0 et h 6= 0
1
1
−α
f (α + h) − f (α)
= α+h
h
h
=
α+h
α
− α(α+h)
α(α+h)
h
α − (α + h) 1
×
=
α(α + h)
h
−h
1
=
×
α(α + h) h
−1
=
α(α + h)
−1
.
α2
On a donc prouvé que quelque soit le nombre α 6= 0, la fonction est dérivable en α et
1
1
f ′ (α) = − 2 . Cela montre bien que la fonction dérivée est définie par f ′ (x) = − 2 .
α
x
donc le taux d’accroissement lorsque h tend vers 0 a pour limite
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
14 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Fonction dérivée
Dérivées des fonctions usuelles
Théorème 4
La fonction racine carrée définie sur [0 ; + ∞[ par f (x) =
]0 ; + ∞[.
p
x est dérivable sur
1
Sa fonction dérivée est définie sur ]0 ; + ∞[ par f ′ (x) = p .
2 x
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
15 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Fonction dérivée
Dérivées des fonctions usuelles
Démonstration
Quels que soient les réels α > 0 et h 6= 0
f (α + h) − f (α)
=
h
=
=
=
=
p
p
α+h− α
h
p
p p
p
( α + h − α)( α + h + α)
p
p
h( α + h + α)
α+h−α
p
p
h( α + h + α)
h
p
p
h( α + h + α)
1
p
p
α+h+ α
1
donc le taux d’accroissement lorsque h tend vers 0 a pour limite p .
2 α
On a donc prouvé que quelque soit le nombre α > 0, la fonction est dérivable en α et
1
1
f ′ (α) = p . Cela montre que la fonction dérivée est définie sur ]0 ; + ∞[ par f ′ (x) = p .
2 α
2 x
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
16 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Fonction dérivée
Dérivées des fonctions usuelles
Théorème 5
n étant un entier naturel non nul.
La fonction définie sur R par f (x) = xn est dérivable sur R.
Sa fonction dérivée est définie sur R par f ′ (x) = n xn−1 .
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
17 / 17
Activité d’introduction
Nombre dérivé et tangente
Fonctions dérivées
Fonction dérivée
Dérivées des fonctions usuelles
Théorème 5
n étant un entier naturel non nul.
La fonction définie sur R par f (x) = xn est dérivable sur R.
Sa fonction dérivée est définie sur R par f ′ (x) = n xn−1 .
Cette propriété sera admise.
Première S ( Lycée du golfe de Saint Tropez)
Dérivation
Année 2015/2016
17 / 17