La mesure des angles

La mesure des angles
 Notion
1. Définition
Un angle est une partie du plan déterminée par deux demi-droites de même
origine.
Remarque : chaque paire de demi-droites définit deux angles.
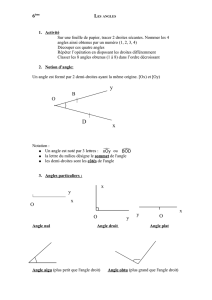
2. Notation et vocabulaire
 et  sont les côtés de l’angle
 est un angle de sommet A, on peut le noter aussi   ou  .
Remarque : par convention, celui que l’on désigne est toujours le plus petit des
deux angles. Si on veut parler du plus grand, il faut obligatoirement le montrer
sur le dessin.
 Classement
1. Amplitude
La mesure d’un angle est déterminée par son ouverture, elle est appelée
amplitude de cet angle.
Remarques :
- L’amplitude d’un angle ne dépend pas de la longueur des côtés.
- L’unité de mesure de l’amplitude d’un angle est le degré, représenté par le
symbole « ° ».
2. Notation
On note l’amplitude de 
 sous la forme  ° ou encore simplement  °

3. Classement
La dynamique de comparaison des angles peut être visualisée sur un schéma ou à
partir d’un éventail à 360°.
4. Définitions
- Un angle est saillant si son amplitude est inférieure à 180°.
- Un angle est rentrant si son amplitude est supérieur à 180°.
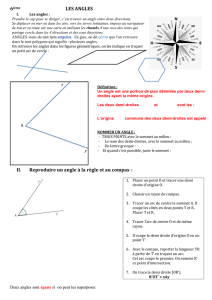
 Mesure, tracé et report d’angles
1. Description
Le rapporteur est l’instrument qui permet de mesurer les angles en degrés.
Certains ont la forme d’un disque, d’autres d’un demi-disque, d’autres sont
incorporés dans une équerre à parallèles.
2. Méthode pour mesurer un angle
Pour mesurer un angle, en utilisant une équerre à parallèles :
1) Placer le repère zéro sur le sommet de l’angle et aligner le grand côté de
l’équerre sur un côté de l’angle ;
2) En partant du zéro de la graduation (attention, choisir le bon !), lire la mesure
de l’angle jusqu’au deuxième côté de l’angle.
Il est parfois nécessaire de prolonger les côtés de l’angle pour lire la graduation.
Exemple :

3. Méthode pou tracer un angle
Pour tracer un angle d’amplitude donnée, il faut :
1) Tracer une demi-droite, qui formera le premier côté de l’angle ;
2) Placer le repère zéro de l’équerre sur l’origine de la demi-droite tracée et le
côté de l’équerre sur la demi-droite ;
3) En partant du zéro de la graduation, pointer la graduation correspondant à
l’amplitude voulue ;
4) Tracer le deuxième côté de l’angle, en joignant le sommet au point placé.
Exemple :
4. Méthode pour reporter un angle
Pour reporter un angle donné, avec le compas
1) En plaçant la pointe sèche du compas sur le sommet A de l’angle, tracer sur
l’angle à reporter un arc de cercle qui coupe les deux côtés de l’angle en deux
points notés B et C.
2) Sur une demi-droite d’origine O, tracer un arc de cercle de centre O, en
gardant la même ouverture de compas. Cet arc de cercle coupe la demi-droite
en Y.
3) Après avoir relevé au compas la longueur  en plaçant les deux pointes du
compas sur les points B et C, tracer un deuxième arc de cercle dont
l’ouverture vaut  et dont le centre est Y. Nommer X l’intersection entre les
deux arcs de cercle.

4) Tracer.
 Angles associés
1. Définitions
- Deux angles sont adjacents lorsque : - ils ont le même sommet ;
- ils ont un côté commun ;
- ils sont situés de part et d’autre de ce
côté commun.
- Deux angles sont complémentaires si la somme de leurs amplitudes vaut 90°.
- Deux angles sont supplémentaires si la somme de leurs amplitudes vaut 180°.
2. Exemples
Paires d’angles
complémentaires
Paires d’angles supplémentaires
Paires d’angles dont la somme
ne vaut ni 90°, ni 180°.
P
A
I
R
E A
S D
J
D’ A
A C
N E
G N
L T
E S
S

P
A
I
R
E
S A
D
D’ J
A A
N C
G E
L N
E T
S S
N
O
N
Angles non adjacents car ils
n’ont pas de côté commun.
Angles non adjacents car ils ne
sont pas situés de part et
d’autre du côté commun.
Angles non adjacents car ils
n’ont pas le même sommet.
 La bissectrice d’un angle
1. Définition
La bissectrice d’un angle est la demi-droite issue du sommet de cet angle et le
partageant en deux angles de la même amplitude.
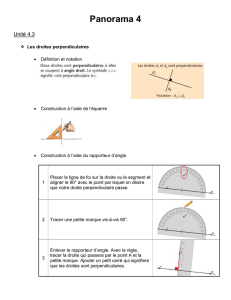
2. Méthode de construction à la règle et au rapporteur