Ae 13 application des lois de newton avec correction bis

Terminale S
AE 13_Application des lois de Newton
M.Meyniel 1/6
APPLICATION DES LOIS DE NEWTON
Objectifs : - Mettre en œuvre une démarche expérimentale pour étudier un mouvement.
- Modéliser/retrouver l’équation horaire paramétrique et l’équation de la trajectoire du mouvement
d’un solide lancé avec une vitesse initiale.
Document 1 : Enoncé des lois de Newton (1 666)
1ère loi : le principe d’inertie
Dans un référentiel galiléen, si le vecteur-vitesse du centre d’inertie G d’un système est un vecteur
constant «  », alors les forces qui s’exercent sur le système s’annulent et réciproquement :
2ème loi : Principe fondamental de la dynamique PFD
Dans un référentiel galiléen, la variation du vecteur-quantité de mouvement d’un système par
rapport au temps est égale à la somme des forces extérieures appliquées à ce système :
On peut également l’écrire :
avec la masse m du système constante.
3ème loi : principe d’action/réaction
Lorsque deux corps A et B sont en interaction, A exerce sur B la force  et B exerce sur A la force
telles que : 
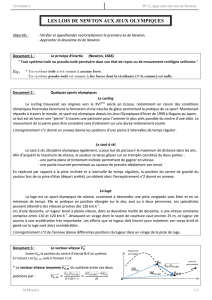
Document 2 : Champ de pesanteur Terrestre 
En première approximation, on peut définir le poids  comme l’action gravitationnelle de la Terre
sur un objet M de masse m, soit pour une altitude z et une latitude : 
Le champ de pesanteur local  est alors tel que :  = m
Avec RT : rayon de la Terre : 6378 km à l’équateur
z : altitude de l’objet M de masse m
: latitude de l’objet M de masse m.
MT : la masse de la Terre: 5,97.1024 kg.
G : constante universelle de gravitation:6,67.10-11 kg-1.m3.s-2
Document 3 : Matériel à disposition
- Logiciel et notice d’utilisation LatisPro® ;
- Video « TP1Schuteparabolique.avi » disponible dans les fichiers LatisPro®.

Terminale S
AE 13_Application des lois de Newton
M.Meyniel 2/6
Travail à faire :
1. Questions préliminaires :
A l’aide des données du document 2 :
a) Donner l’expression vectorielle du champ de pesanteur 
 au niveau du sol. Préciser ses
caractéristiques : direction, sens et intensité. Ce champ est aussi appelé « accélération de pesanteur ».
b) En-dessous de quelle altitude ce champ de gravitation peut-il être considéré comme
uniforme ? Information : On considèrera le critère suivant : le champ est considéré
comme uniforme si sa norme ne varie pas de plus de 1 %.
2)
a) Proposer un protocole expérimental utilisant les logiciels mis à disposition pour obtenir les
équations horaires numériques des coordonnées : - x
y du vecteur-position OG
;
- vx
vy du vecteur-vitesse v ;
- ax
ay du vecteur-accélération a
.
Faire vérifier votre protocole par le professeur.
b) Réaliser ce protocole sur la vidéo citée dans le document 3, en utilisant le logiciel LatisPro®
ainsi que la notice d’utilisation associée.
Sur votre feuille, représenter l’allure des graphiques obtenus ainsi que les expressions des
fonctions modélisées.
Faire vérifier vos résultats par le professeur.
c) A l’aide l’ensemble de vos résultats, déterminer :
- les coordonnées du vecteur-vitesse initial  de la balle ainsi que sa norme ;
- l’angle α formé par le vecteur-vitesse initial et l'horizontale ;
- la valeur moyenne du champ de pesanteur terrestre  .
Faire vérifier vos résultats par le professeur.
d) A partir d’un bilan des forces et de la deuxième loi de Newton appliquée sur le système balle,
vérifier les relations modélisées.
Faire vérifier vos résultats par le professeur.
du centre G de
cette balle.

Terminale S
AE 13_Application des lois de Newton
M.Meyniel 3/6
CORRECTION
1) a) D’après l’énoncé : 
Or : 
=> 
En se plaçant au niveau du sol : « z = 0 ». L’expression devient : 
Le champ de pesanteur  a donc : - pour direction  soit vertical au sol (d’après le schéma) ;
- un sens opposé à celui de  donc vers le centre de la Terre ;
- une intensité :  
 9,79 N.kg-1
b) Le champ est considéré comme uniforme si son intensité ne varie pas de plus de 1 %.
Il faut donc calculer l’altitude « z » pour laquelle on a : « g(z) = 
 g0 »
g(z) = 
 g0
g(z)  
 =>    => (RT + z)² = 
=> z = 
 - RT
=> z =
 - 6 378.103 = 32.103 m
On peut donc estimer que le champ de pesanteur est uniforme jusqu’à une altitude de 32 km !
2) Protocole expérimental :
 Ouvrir la vidéo avec le logiciel LatisPro®.
 Après avoir choisi l’origine et étalonner l’image, réaliser le pointage de la balle.
 Basculer sur la fenêtre avec les courbes et placer les points obtenus pour « x » et pour
« y » afin de visualiser respectivement les courbes « x = f(t) » et « y = f(t) ».
 Modéliser chacune de ces courbes pour obtenir leurs équations.
 Pour obtenir l’expression des coordonnées « vx » et pour « vy » du vecteur-vitesse :
Cliquer sur Traitements → Calculs spécifiques → Dérivée puis glisser la
fonction à dériver : « x = f(t) » pour obtenir « vx = f(t) » et « y = f(t) » pour obtenir
« vy = f(t) ».
Modéliser chacune de ces courbes pour obtenir leurs équations.
 Refaire le même travail pour obtenir l’expression des coordonnées « ax » et pour « ay »
du vecteur-accélération :
Cliquer sur Traitements → Calculs spécifiques → Dérivée puis glisser la
fonction à dériver : « x = f(t) » pour obtenir « vx = f(t) » et « y = f(t) » pour obtenir
« vy = f(t) ».
Modéliser chacune de ces courbes pour obtenir leurs équations.

Terminale S
AE 13_Application des lois de Newton
M.Meyniel 4/6
Pointage de la balle sur la vidéo :
b)
* Equation horaire des coordonnées du vecteur-position :
On modélise la courbe « x = f(t) » par une fonction linéaire : x = 1,747 × t
On modélise la courbe « y = f(t) » par une fonction linéaire : y = - 4,921 × t² + 4,434 × t +17,5.10-3
* Equation horaire des coordonnées du vecteur-vitesse :
On modélise la courbe « vx = f(t) » par une fonction linéaire : vx = 1,747
On modélise la courbe « vy = f(t) » par une fonction linéaire : vy = - 9,972 × t + 4,526

Terminale S
AE 13_Application des lois de Newton
M.Meyniel 5/6
* Equation horaire des coordonnées du vecteur-vitesse :
On modélise la courbe « ax = f(t) » par une fonction linéaire : ax ≈ 0
On modélise la courbe « ay = f(t) » par une fonction linéaire : ay = - 10,018
c)
* D’après le schéma, on en déduit en utilisant le théorème de Pythagore : V02 = vx02 + vy02
 ²² = ²²4,851 m.s-1
Rq : Pour les valeurs de « vx0 » et « vy0 », on reprend les équations horaires de « vx » et « vy » en prenant « t = 0 ».
* D’après le schéma, on en déduit en utilisant la trigonométrie : tan(α) = vy0 / vx0
 tan(α) = vy0 / vx0 = 4,526 / 1,747 = 2,591 => α = arctan(2,591) = 68,89 °
Rq : Attention à avoir la calculatrice en « mode degré ».
* Le champ de pesanteur « g » est une accélération. Ici, comme il s’agit d’une chute libre, le champ de
pesanteur est égal à l’accélération (Cf question d.) : a = g
 ²²= ²²10,018 m.s-2
Rq : Pour les valeurs de « ax » et « ay », on reprend les équations horaires de « ax » et « ay ».
x
y
vx0
vy0
α