Télécharger le fichier

Panorama 8
Unité 8.2-2
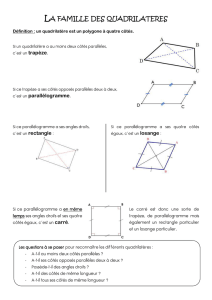
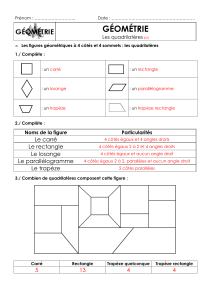
 La construction de quadrilatères
 Carré
Il faut seulement la mesure d’un côté.
 Rectangle
Il faut la mesure des deux côtés.
 Parallélogramme
Il faut deux mesures de côtés et une mesure d’angle.
o Exemple : trace un parallélogramme ABCD dont les côtés mesurent 5 cm et 3 cm
et la mesure de l’angle ABC est 70°.
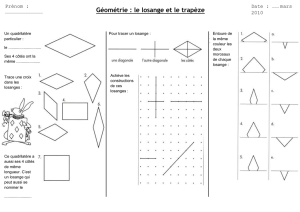
 Losange
Il faut la mesure d’un côté et d’un angle.
o Exemple : trace un losange EFGH dont un côté mesure 4 cm et la mesure de
l’angle FEH est de 50°.

Ou
Il faut la mesure des deux diagonales.
o Exemple : trace un losange KLMN dont les diagonales mesurent 3 cm et 5 cm.
 Trapèze rectangle
Il faut la mesure de trois côtés dont la hauteur.
o Exemple : trace le trapèze rectangle RSTU dont les côtés parallèles mesurent 4
cm et 2 cm et la hauteur mesure 3 cm.
 Trapèze isocèle
Il faut la mesure de trois côtés et une mesure d’angle.
o Exemple : trace le trapèze isocèle VWXY dont les côtés parallèles mesurent : m
YX
̅
̅
̅
̅
= 7 cm et m VW
̅
̅
̅
̅
̅
= 3,5 cm, la mesure d’un côté non parallèle est m YV
̅
̅
̅
̅
= 2,7
cm et l’angle VYX mesure 50°.

 Énoncés mathématiques sur les quadrilatères
 La somme des mesures des angles intérieurs d’un quadrilatère est 360°.
 Dans tout trapèze, les deux angles adjacents aux côtés non parallèles sont
supplémentaires.
m ∠DAB + m ∠ADC = 180°
m ∠ABC + m ∠BCD = 180°
 Dans tout trapèze isocèle, les angles opposés sont supplémentaires.
m ∠DAB + m ∠DCB = 180°
m ∠ADC + m ∠ABC = 180°
 Dans tout trapèze isocèle, les deux angles adjacents aux côtés parallèles (les bases)
sont isométriques.
m ∠DAB = m ∠ABC
m ∠ADC = m ∠DCB
 Les angles opposés d’un parallélogramme et d’un losange sont isométriques.
m ∠DAB = m ∠BCD
m ∠ADC = m ∠ABC

 Les angles consécutifs d’un parallélogramme et d’un losange sont supplémentaires.
m ∠DAB + m ∠ABC = 180°
m ∠ADC + m ∠DCB = 180°
m ∠DCB + m ∠ABC = 180°
m ∠ADC + m ∠DAB = 180°
 Les côtés opposés d’un parallélogramme sont isométriques.
m 𝐴𝐵 = m 𝐷𝐶
m 𝐴𝐷 = m 𝐵𝐶
 Tous les côtés d’un losange et d’un carré sont isométriques.
m 𝐴𝐵 = m 𝐵𝐶 = m 𝐶𝐷 = m 𝐷𝐴

 Tous les angles d’un rectangle et d’un carré sont isométriques.
m ∠DAB = m ∠ABC = m ∠BCD = m ∠CDA
 Les diagonales d’un parallélogramme, d’un losange, d’un rectangle et d’un carré se
coupent en leur milieu.
m 𝐴𝑀 = m 𝑀𝐶
m 𝐷𝑀 = m 𝑀𝐵
 Les diagonales d’un trapèze isocèle, d’un rectangle et d’un carré sont isométriques.
m 𝐴𝐶 = m 𝐷𝐵
 Les diagonales d’un losange et d’un carré sont perpendiculaires.
m ∠DMA = m ∠AMB = m ∠BMC = m ∠CMD = 90°