La formule de Moivre et la formule d`Euler

La formule de Moivre
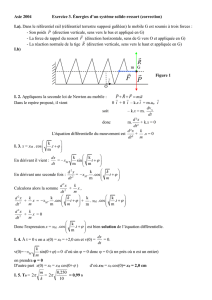
Rappel. A tout nombre complexe non nul z = a + ib , écrit sous
forme cartésienne algébrique l’on peut associer un couple (r, θ)
où r = z = z ! z = a 2 + b2 est appelé son module (en quelque
sorte la norme du vecteur z) et θ correspond à l’angle orienté
(dans le sens trigonométrique) entre 1 + i0 et a + ib. On appelle
argument de z l’angle en question et on a 0 ! arg(z) = " < 2# .
Ainsi :
z = a + ib = r(cos(! ) + isin(! )) .
Cette écriture s’appelle polaire trigonométrique (ou cis(z)).
cf. le croquis ci-contre (http://fr.wikipedia.org/wiki/Nombre_complexe)
Exercice 1. a) Convertir sous forme d’écriture polaire trigonométrique les complexes suivants :
1) a =
2
2
+i
2
2
2) b = 3 ! i
3) c = -1 + i
4) d = -2 – 2i
b) Si |z| = ½ et arg(z) = 5π / 6 déterminer la forme cartésienne algébrique de z.
Théorème de Moivre (1730)
a) Si z1 = r1 (cos(!1 ) + isin(!1 )) et z2 = r2 (cos(! 2 ) + isin(! 2 )) alors z1z2 = r1r2 (cos(!1 + ! 2 ) + isin(!1 + ! 2 ))
b) Si z = r(cos(! ) + isin(! )) et n !! alors z n = r n (cos(n! ) + isin(n! )) .
Ainsi le produit de deux nombres complexes est le complexe de module leur produit et d’argument
leur somme.
Preuve. Par les formules d’addition de trigonométrie z1z2 = r1r2 (cos(!1 ) + isin(!1 ))(cos(! 2 ) + isin(! 2 )) =
= r1r2 #$cos(!1 )cos(! 2 ) " sin(!1 )sin(! 2 ) + i(cos(!1 )sin(! 2 ) + sin(!1 )cos(! 2 ) %& = r1r2 #$cos(!1 + ! 2 ) + isin(!1 + ! 2 ) %& .
Ainsi si z = r(cos(! ) + isin(! )) alors par a) appliqué n fois z n = r n (cos(n! ) + isin(n! )) où plus
rigoureusement en effectuant une récurrence sur n.
Exercice 2. Résoudre les équations ci-dessous en donnant les solutions sous forme trigonométrique.
1) z 6 = 1
2) z 4 + 1 = 0
3) 4z 5 ! 128 = 0
4) z 5 + z 4 + z 3 + z 2 + z + 1 = 0
Exercice 3. Représenter dans le plan complexe les nombres a, b, c et d. Puis, sans calculer,
localiser dans le plan complexe les nombres a·b , a·c , a·d , 1 / a , -a et -a .
Exercice 4. Soit le triangle représenté par les trois nombres complexes : a = 1– 2i ; b = 3 – i
et c = -1 + 2i. Montrer que le triangle est rectangle et calculer son aire.
On considère la fonction f : z ! (2 ! i) " z ! 1 .
A quoi ressemble l’image du triangle précédent par f et quelle est son aire ?
Exercice 5. Démontrer rigoureusement la formule de Moivre en effectuant une récurrence sur n.
Exercice 6. Factoriser les polynômes ci-dessous dans ![z] et identifier leurs racines.
P1 (z) = z 4 + z 3 + z 2 + z + 1
P2 (z) = z 6 + z 4 + z 2 + 1
La formule d’Euler
Dans le chapitre VII de son Introductio in analysin infinitorum (1748), Euler expose une méthode
pour obtenir le développement de la fonction réelle exponentielle en série entière au voisinage de 0.
Une approche moderne permet d’obtenir le résultat en intégrant par parties n-fois puis en majorant
le reste intégral :
x
x
0
0
e x ! 1 = " et dt = " 1! $ et dt = !(x ! t) $ et
"#
$ $
%
f#
= x+
f1
1
2
x
1
!
(x ! t)3 $ et
2 "2$
$3
$#$$
%
0
x
1
+ " (x
! t) $ et dt = x ! (x ! t)2 $ et
!
"2$#$%
0
f 2#
f2
x
0
x
2
2
x
0
x
1
+ " (x ! t)2 $ et dt
2$#$
%
0 "
f3#
3
1
x
x
1
(x ! t)3 $ et dt = x + +
!
(x ! t)4 $ et
2
$3
2
2
$3
2
3
4
"$#$%
0 "$#$%
+"
f 4#
f3
= par récurrence... = x +
x
3
4
f4
n
x
0
x
1
(x ! t)4 $ et dt =
2
3
4
0 "$#$%
+"
f5#
x
x
x x
x
1
+ + + ...+ + " (t ! x) n $ et dt
2! 3! 4!
n! n! 0
"$$#$$%
Rn
Comme vu en classe lim
n!"
n
a
= 0 permet de démontrer alors que le reste intégral tend vers 0.
n!
x2 x3 x4
xn
D’où e x = 1+ x + + + + ...+ + ....
2! 3! 4!
n!
D’une manière tout à fait similaire l’on peut prouver que :
sin(x) = x !
x3 x5 x7
x 2n+1
+ ! ± ...+ (!1) n
+ .... et
3! 5! 7!
(2n + 1)!
x2 x4 x6
x 2n
+ ! ± ...+ (!1) n
+ ....
2! 4! 6!
(2n)!
Euler n’hésite pas à franchir un pas audacieux en substituant à x (réel) une variable complexe i! :
ei! = 1+ i! "
# !2 !4 !6
& #
&
!2 !3 !4 !5
!3 !5 !7
" i + + i ± ... = % 1" + " ± ...( + i % ! " + " ± ...( = cos(! ) + isin(! ) .
2!
3! 4!
5!
2! 4! 6!
3! 5! 7!
$
' $
'
cos(x) = 1!
Cas particulier en prenant ! = " on obtient : ei! = cos(! ) + isin(! ) = "1 ou ei! + 1 = 0 , réunissant en
une égalité quatre constantes célèbres : les éléments neutres additifs et multiplicatif, le rapport de la
circonférence du cercle à son diamètre et l’unité imaginaire.
cos(x) + isin(x)
pour des x réels.
eix
(" sin(x) + icos(x))eix " i #(cos(x) + isin(x))eix
= 0.
La dérivée de f est f !(x) =
(eix )2
Autre pseudo-preuve. Posons f (x) =
Par le corollaire de Lagrange f est donc une constante. Posons x = 0 et l’on voit que f(0)=1.
D’où
Théorème d’Euler (1748) : pour tout θ dans ! on a ei! = cos(! ) + isin(! )
Dans les deux cas ci-dessus la rigueur des preuves laisse à désirer : dans le premier on manipule des
séries infinies (commutativité, associativité) comme s’il n’y avait qu’un nombre fini de termes, sans
trop se préoccuper de problèmes de convergence. Dans la deuxième, on emploie des règles de
dérivation vraies pour des fonctions purement réelles, alors qu’ici la fonction ! ! " , de même en
ce qui concerne l’utilisation de Lagrange. N’empêche que l’intuition d’Euler était correcte. Tous ces
concepts peuvent être étendus au plan complexe. Suites, séries, fonctions complexes, dérivation et
intégrales curvilignes et de surface se généralisent tous (avec quelques précautions) au domaine de
l’ANALYSE COMPLEXE, dont Augustin Cauchy (1789 -1857) sera l’un des pères fondateurs.
Quelques conséquences du théorème d’Euler
Tout nombre complexe admet alors une troisième écriture :
z = a + ib = r(cos(! ) + isin(! ))= r ei! que l’on appelle sous forme polaire exponentielle.
eix ! e! ix
eix + e! ix
et cos(x) =
2i
2
i!
Preuve. Dans la formule e = cos(! ) + isin(! ) remplaçons θ par x puis par -x d’où le syst. d’équa.
Théorème. Si x !! alors sin(x) =
"$ eix = cos(x) + isin(x)
"$ eix = cos(x) + isin(x)
& # ! ix
que l’on résous par addition.
# ! ix
$% e = cos(!x) + isin(!x)
$% e = cos(x) ! isin(x)
Résolution d’équations complexes particulières.
L’écriture sous forme polaire exponentielle permet de résoudre instantanément certaines équations.
1) z n = 1 !
( re )
i"
n
= 1 ! ei" n = 1 = e2ik# ! " = 2k# / n où k = 1,2,...,n
(
)
i
2) z = i i . Mais i = ei(! /2+2k! ) . D’où z = ei(! /2+2k! ) = e"(! /2+2k! ) avec k #! .
Exercice 36 à 40 de la brochure Complexes de M. Cuénod.
Construction du corps des nombres complexes par Hamilton.
Hamilton (1843) considère l’ensemble ! ! ! sur lequel il définit deux opérations :
+ : ( (a;b);(c;d) ) ! ( a + c;b + d ) et i : ( (a;b);(c;d) ) ! ( ac ! bd;ad + bc ) .
Exercice. Montrer que + et · font de ! ! ! un corps.
Prouver la commutativité, l’associativité des deux opérations, identifier les éléments neutres,
identifier l’opposé et l’inverse (d’un non nul) puis prouver la distributivité de la multiplication sur
l’addition. Enfin établir l’isomorphisme avec ! = {a + ib ; a et b !"} .
Construction du corps des nombres complexes par Cauchy.
Cauchy (vers 1820) considère l’ensemble des polynômes à coefficients réels ![x] . L’addition et la
multiplication de polynômes se fait de manière habituelle. Puis, il définit une relation d’équivalence
sur l’ensemble des polynômes : P ~ Q (est équivalent) si et seulement si x2 + 1 divise P – Q.
Exercice. Montrer que ~ est bien une relation d’équivalence (réflexif, symétrique et transitif).
L’ensemble des polynômes équivalents à un polynôme P sera dénoté P , que l’on appellera la
classe de P. Pour déterminer le polynôme de degré minimal représentant un polynôme donné P il
suffit de considérer le reste de la division euclidienne de P par x2 + 1 .
Exemple. x 3 + 2x + 1 = x(x 2 + 1) + x + 1 ! x + 1
Ainsi l’ensemble des représentants (de degré minimal) des classes est constitué de polynômes au
plus de degré 1. L’on peut montrer que l’addition et la multiplication sont compatibles sur les
classes et font de l’ensemble quotient ![x] / (x 2 + 1) un corps isomorphe à ! .
ATTENTION AUX GENERALISATIONS
Le paradoxe de Gabriel : 4 ! ln(i) = ln(i 4 ) = ln(1) = 0 d’où ln(i)=0. Alors que i = eln(i) = e0 = 1 ?
Le paradoxe ci-dessus prend appui sur le faux théorème ci-dessous, qui admet évidemment une
fausse preuve !
Faux théorème. ln(z1z2 ) = ln(z1 ) + ln(z2 ) pour tous les complexes z1 , z2 non nuls.
Fausse preuve. Mettons zk sous forme polaire exponentielle : zk = rk ei! k =1 et 2.
k
ln(z1z2 ) = ln(r1ei!1 r2 ei! 2 ) = ln(r1r2 ei(!1+! 2 ) ) = ln(eln(r1r2 ) ei(!1+! 2 ) ) = ln(eln(r1r2 )+i(!1+! 2 ) ) = ln(r1r2 ) + i(!1 + ! 2 ) par ailleurs
ln(z1 ) + ln(z2 ) = ln(r1ei!1 ) + ln(r2 ei! 2 ) = ln(eln(r1 ) ei!1 ) + ln(eln(r2 ) ei! 2 ) = ln(eln(r1 )+i!1 ) + ln(eln(r2 )+i! 2 ) = ln(r1r2 ) + i(!1 + ! 2 )
Où se situent la ou les erreurs ? Elles proviennent toutes du fait que l’on attribue ingénument les
propriétés de la fonction réelle ln à ‘la’ fonction logarithme sur les complexes.
Eclaircissement. La fonction réelle ex est une bijection de ! ! !*+ dont la réciproque est notée
ln(x). Or nous venons de ‘démontrer’ que ei! = cos(! ) + isin(! ) d’où ei! = ei(! +2k" ) et donc sur les
complexes la fonction e z est 2iπ-périodique (sur les « lignes imaginaires »). Elle n’est donc
absolument pas bijective ! Ainsi, si e z = w on dira que z est un logarithme de w. Mais il en existe
bien d’autres : z + 2ik! où k est un entier. Par exemple, les logarithmes de 1 sont les nombres 2ik! ,
les logarithmes de -1 sont les nombres i! + 2ik! , et les logarithmes de i sont les nombres
i!
+ 2ik! .
2
Définition d’une fonction logarithme particulière : Log(w)
Pour rendre la fonction e z injective on peut délimiter son ensemble de départ à une « bande
horizontale » de largeur 2π, en prenant par exemple le sous-ensemble
D := { z = a + ib !! ; a !" et b !] " # ;+# ]} .
Affirmation. La fonction e z : D ! ! est une bijection dont nous dénoterons l’inverse par Log.
Preuve. 1) Injectivité : Supposons que e z = e z . Comme e z = ea+ib = ea eib = ea !1 = eRe( z ) = eRe( z ) l’on
1
2
en déduit que z1 et z2 ont même partie réelle (car e x est une fonction réelle bijective). Par ailleurs*,
Arg(e z ) = Arg(e a+ib ) = Arg(e a ! eib ) = Arg e a !(cos(b) + isin(b)) = Arg ( cos(b) + isin(b) ) = b = Im(z) .
(
)
D’où Im(z1) = Im(z2) et donc z1 = z2 .
2) Surjectivité : Soit un w = a + ib dans ! quelconque. Par les calculs précédents si e z = w alors
| w | =| e z | = e Re( z ) et Arg(e z ) = Im(z) , en d’autres termes z = Re(z) + i ! Im(z) = ln | w | + i ! Arg(w) .
D’où la définition du Log : ! ! D par Log(w) = ln | w | +i ! Arg(w) .
Exercices.
a) Représenter les deux plans complexes ci-dessous de la fonction exp et hachurer d’autres
domaines sur lesquels la fonction e x : ! ! ! est bijective.
b) Expliciter précisément les erreurs commises dans les fausses affirmations du haut de la page.
c) Est-il vrai que (exp ! Log)(z) = z et que (Log ! exp)(z) = z pour tous z non nul dans ! ?
d) Quel est l’ensemble image de l’intervalle { a + ib ; a !! fixé et b !] " # ;+# ]} par la fonction e z .
*
L’Arg(z) n’est autre que l’angle mesuré non entre [0 ; 2π[ mais entre ]-π ; π].
Correction de quelques exercices.
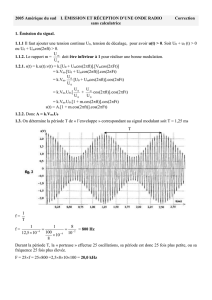
Ex 4. Soit le triangle représenté par les trois nombres complexes : a = 1– 2i ; b = 3 – i
et c = -1 + 2i. Montrer que le triangle est rectangle et calculer son aire.
On considère la fonction f : z ! (2 ! i) " z ! 1 .
A quoi ressemble l’image du triangle précédent par f et quelle est son aire ?
Correction. A l’exception du i l’exercice est presque de 9e année (si deux droites affines sont
perpendiculaires alors le produit de leur pente = -1 et réciproquement) : ½ · (-2) = -1
De plus le produit de a, b et c par un complexe k = 2 – i n’est autre qu’une rotation et une
homothétie de rapport le module de k. Le nouveau triangle est donc toujours rectangle.
Illustration de la situation. aire départ : 8 et |2 – i |2 = 5 d’où nouvelle aire 40.
Départ
Arrivée
Correction ex. 6 : Factoriser les polynômes ci-dessous dans ![z] et identifier leurs racines.
P1 (z) = z 4 + z 3 + z 2 + z + 1
P2 (z) = z 6 + z 4 + z 2 + 1
En utilisant les racines de l’unités e2i! k /n où 0 ≤ k ≤ n – 1.
a) Si on multiplie P1 par z – 1 alors on obtient z5 – 1 =
4
# (z ! e
2i" k /5
k=0
b) P2 (z) = z + z + z + 1 = (z + 1)(z + 1) = (z ! e
6
4
2
2
4
i" /2
)(z ! e
! i" /2
)(z ! e
4
) d’où P1 (z) = # (z ! e2i" k /5 )
k=1
i" /4
)(z ! e
3i" /4
5i" /4
)(z ! e
)(z ! e7i" /4 )