´Etude du mouvement d`une particule chargée dans un champs

´
Etude du mouvement d’une particule charg´ee
dans un champs ´electromagn´etique
MPSI
16 juin 2008

Table des mati`eres
1 Force de Lorentz 2
1.1 Champs ´electrique, champs magn´etique . . . . . . . . . . . . . 2
1.2 ForcedeLorentz ......................... 2
1.3 Invarience relativiste . . . . . . . . . . . . . . . . . . . . . . . 2
2 Mouvement d’une particule charg´e dans un champs ´elec-
trique 4
2.1 Trajectoire............................. 4
2.2 Focalisation ............................ 4
2.3 Canon`a´electrons......................... 5
3´ Etude du mouvement d’une particule charg´ee dans un champs
magn´etique 6
1

Chapitre 1
Force de Lorentz
1.1 Champs ´electrique, champs magn´etique
D´efinition 1 A chaque fois qu’on d´etecte une difference de potentiel entre
deux points de l’espace, on introduit une grandeur vectorielle, appel´e champs
´electrique, not´ee −→ E, d’unit´e Volt/metre
D´efinition 2 Un aimant ou un circuit parcouru par un courant peux avoir
une action sur une boussole. On mod´elise cette action par un champs ma-
gn´etique, not´ee −→ B, d’unit´e le Tesla.
1.2 Force de Lorentz
D´efinition 3 Soit M(m,q) une particule charg´ee observ´e dans le r´ef´erentiel
R galil´een.
Si M est plong´ee dans la zone d’action d’un champs ´electromagn´etique (−→ E , −→ B),
elle subit la force de Lorentz :
−→
Fl=q(−→ E+−→ v(M)R∧−→ B)
1.3 Invarience relativiste
Propri´et´e 1 On peut d´efinir un r´ef´erentiel R’ dans lequel −→ E0=−→ 0.
On obtient donc que le champs −→ Eet −→ Bne suffisent pas, on prend donc en
compte le couple : (−→ E , −→ B).
2

Propri´et´e 2 Dans l’´etude des particules ´elementaires, on n´eglige l’influence
de son poids.
3

Chapitre 2
Mouvement d’une particule charg´e
dans un champs ´electrique
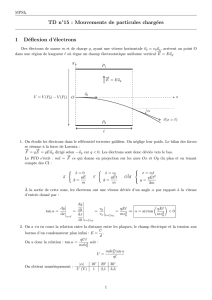
2.1 Trajectoire
Soit M(m,e−) un ´electron assimil´e `a un point materiel observ´e dans R
galil´een.
On obtient, par application du P.F.D, l’´equation horaire :
y(x) = e.E
m.v2
0
.x2
La trajectoire est donc une parabole.
2.2 Focalisation
Consid´erons un faisceau de particules charg´ees passant dans la zone d’ac-
tion de −→ E=E.−→ i, avec un vecteur vitesse −→ v0=v0.cos(α).−→ i+v0.sin(α).−→ j,
on obtient :
x(y) = −EC
2.m.(v0.sin(α))2.y(t)2+y(t) tan(α)
On obtient la port´e maximale, pour x(y) = 0 et y 6= 0 :
yp=m.v2
0
e.E .sin(2α)
La port´ee est maximale pour α=π
4. Pour des angles proche de α, le faisceau
focalise toujours en yp.
4