Les TD - Université Jean Monnet

CITSE 2 Université Jean-Monnet-Télécom St-Etienne
TD Phénomènes vibratoires 2009-2010
N°1
Exercice 1
On considère un oscillateur mécanique amorti constitué d'une masse m attachée à l'extrémité
d'un ressort horizontal, l'autre extrémité étant fixe.
Le système est en oscillation et on mesure la position instantanée de la masse. Le graphe
suivant décrit cette évolution.
1. Quel est le régime d'évolution de l'oscillateur ? Donner l'équation différentielle faisant
intervenir le coefficient d'amortissement  et la pulsation propre 0 à laquelle satisfait
x(t). Donner l'expression générale de x(t).
2. Déterminer graphiquement la pseudo-période d'oscillation que l'on notera T1.
3. On rappelle que le décrément logarithmique est donné par
1
1x(t)
ln
nx(tnT)
 .
Déterminez-le graphiquement, puis exprimez-le littéralement en fonction du
coefficient d'amortissement et de la pseudo-période.
4. Déduire les valeurs du coefficient d'amortissement, de la période propre et du facteur
de qualité.

CITSE 2 Université Jean-Monnet-Télécom St-Etienne
Exercice 2
Un piston de section S, de masse m, mobile sans frottement dans un cylindre, emprisonne au
repos un volume V0 d’air sous la pression atmosphérique P0 et à la température T0. On donne
une impulsion sur le piston initialement immobile. On néglige la viscosité de l’air.
1. Dans l’hypothèse où la masse d’air emprisonnée suit la loi d’évolution adiabatique
P.V=cte, établir différentielle en x(t) qui régit le mouvement du piston.
On prendra |V’|<<V0, |P’|<<P0, |T’|<<T0.
2. Calculer la pulsation propre 0. De quel type de régime s’agit-il ?
S, m
V0
P0
P0
T0
T0
0 x
V=V0+V’
P0
P=P0+P’
T0
T=T0+T’
Exercice 3
Un microphone électrodynamique est constitué d'une bobine mobile, de longueur l, reliée au
boîtier par une membrane élastique (fig. 1). L'ensemble mobile sera noté D dans la suite (sa
masse est m, sa vitesse est , il est relié à un bâti fixe par un ressort de raideur k et soumis à
une force de frottement = - f , f > 0). Les spires de la bobine sont en permanence
plongées dans un champ magnétique radial
v
F
1
v
B de module constant (fig. 2). Les deux
extrémités de la bobine sont reliées à un conducteur ohmique de résistance R (non représenté
sur la figure 2) pour former un circuit fermé. Le déplacement de D sous l'action des ondes
sonores provoque l'apparition d'un courant d'intensité i dans le circuit.
Figure 1 Figure 2

CITSE 2 Université Jean-Monnet-Télécom St-Etienne
Ce courant est créé par le phénomène d’induction magnétique et son expression est donnée
par : Blv
iR
La force agissant sur D est la somme d'une force
F
2
a
F = Fa u d'origine acoustique et d'une
force = Fe =
e
F u
22
Blv
R
 u d'origine électromagnétique ( u vecteur unitaire porté par l'axe
Ox de la bobine).
1. Déterminer l'équation différentielle vérifiée par x.
Montrer que cette équation différentielle peut se mettre sous la forme :
a
Fkxx'fxm  
Donner f' en fonction de f, B, l et R.
2. Une onde sonore sinusoïdale est envoyée sur le microphone et crée une force
a
F = Fa cos(t) u . Calculer, en régime permanent, la tension uR aux bornes du
conducteur ohmique, signal électrique fourni par le microphone. On écrira
uR = URM cos(t + ').
3. Application numérique : m = 10-3 kg ; k = 104 N.m-1. Calculer la fréquence No, pour
laquelle URM est maximal.
Exercice 4 : ensemble de poulies
Chercher la fréquence propre du système en admettant que le fil est inextensible et que les
poulies ont une masse nulle
k
1
k
1x1
x
k
2
x2
x1
T
T
T
m
x
m
Exercice 5 : cylindre lesté
Le système pendulaire ci-dessus roule
sans glisser sur un plan horizontal. Il est
constitué d’un cylindre de masse M, de
moment d’inertie J, relié rigidement par
une tige à une masse m supposée
ponctuelle. La masse de la tige étant
négligeable, établir, par dérivation de
l’énergie mécanique, l’équation
C
’
C
x
O O
’
y
L
m
A
’
A

CITSE 2 Université Jean-Monnet-Télécom St-Etienne
différentielle des petits mouvements
autour de la position d’équilibre.
Rappels :
L’énergie ménanique est la somme de l’énergie cinétique et de l’énergie potentielle.
L’énergie du système est la somme de l’énergie de la masse et de l’énergie du cylindre.
Pour le cylindre, l’énergie cinétique présente une composante liée à la translation du centre
d’inertie et une composante liée à la rotation du cylindre.
Exercice 6 : mesure du coefficient de viscosité d’un liquide
Une masse sphérique de centre C, de rayon R, de
masse volumique  est suspendue en O par un fil de
masse négligeable de longueur L = OC. Elle est
complètement immergée dans de l’huile de masse
volumique ’. On supposera R<<L et ’<< .
Etablir l’équation différentielle du mouvement de ce
pendule.
On donne l’expression de la force de frottement
visqueux : 6
fc
FR  V
Où  est le coefficient de viscosité dynamique de
l’huile.
Déterminer  pour que ce pendule soit à
l’amortissement critique.
Exercice 7 : Puissances et énergies en régime forcé
=7800 kg/m3
’=970 kg/m3
R=10 cm
L=0,98 m
g=9,81 m/s²
huile
O
C
L
On donne l’équation du mouvement d’un pendule à ressort en oscillations forcées :
mx cx kx F cos t 
Dont la solution est x=Xcos(t-)
On désigne les forces d’inertie, de frottement, d’élasticité et d’action extérieure de la source
par :
i
f
el
ext
Fmx
Fcx
Fkx
FFcos
t
1- Calculer la puissance instantanée et la puissance moyenne par rapport au temps, mise en
œuvre par chacune de ces sources.
2- Ecrire le bilan de ces puissances et en déduire une expression de sin  en fonction de X, c,
F et . Retrouver l’expression de la puissance réactive.
3- En intégrant chaque puissance et en choisissant conventionnellement la plus petite
constante d’intégration qui rende chaque énergie positive ou nulle, calculer les travaux des 4
forces précédentes. Interpréter.
4- Calculer les rapports d’énergies suivants :
R1=Wi(cinétique maxi)/Ws(dissipée pendant une période T)
R2=Wélas(potentielle maxi)/Ws
en fonction de Q et =/0.
Exercice 8 : Pendule

CITSE 2 Université Jean-Monnet-Télécom St-Etienne
On considère le mouvement d'un pendule simple qui oscille dans un milieu où les forces de frottement
sont inexistantes.
Le pendule est constitué d'un objet ponctuel M de masse m, accroché par l'intermédiaire d'un fil rigide
au point O fixe. On suppose le fil rigide sans masse. L'ensemble est plongé dans le champ de pesanteur
terrestre uniforme. On écarte le fil de sa position d'équilibre d'un angle q(t=0) = q0 et on le lâche sans
vitesse initiale.
OM=l=1,0 m
Oscillations de faible amplitude :
1. Enoncer le théorème du moment cinétique appliqué à un point matériel.
2. Etablir l'équation différentielle vérifiée par l'angle (t) en fonction du temps. Donner
l'expression de la pulsation 0 du mouvement.
3. On mesure pour 20 périodes une durée de 40,12 s. En déduire la valeur de g.
Cas général :
On se place dans le cas d'oscillations d'amplitude plus importante. On désigne par Em l'énergie
mécanique, Ep l'énergie potentielle et Ec l'énergie cinétique du pendule.
1. Donner les expressions des énergies cinétique et potentielle en fonction de m, g,l ,  et d/dt.
On prend l'origine de l'énergie potentielle pour  = 0.
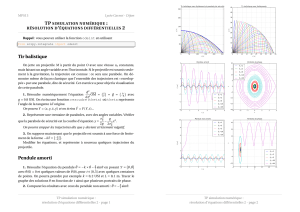
2. En déduire que l'équation de la trajectoire dans le plan de phase du point P de coordonées  (t)
et y = 1/0d/dt peut se mettre sous la forme : y2 + 2(1-cos) = 2Em/ (mgl).
L'allure générale du portrait de phase de cette équation est donnée ci-dessous :
3. Quelles sont les trajectoires de phase correspondant à Em<2mgl ?
4. A quelle situation correspondent les points A ?
5. Quelles sont les courbes correspondant :
- à un mouvement oscillatoire périodique autour d'une position d'équilibre stable ?
- A un mouvement de révolution.
Exercice 9 : Circuit RLC
On considère un circuit électrique RLC composé de trois éléments montés en série : un condensateur
C, une bobine L de résistance interne négligeable et une résistance variable R. On donne C=10µF et
L=100mH.
Le condensateur est initialement chargé. A l'instant t=0, on ferme l'interrupteur K et on laisse le
système évoluer librement. On rappelle que la tension aux bornes du condensateur satisfait à l'équation