Exercice 2 - Ecole sur le Web

0 ? LES SIGNAUX PERIODIQUES EN
MEDECINE
J’applique mes connaissances
Exercice 1
1) Parmi les signaux suivants, indiquer ceux qui sont périodiques et ceux qui
ne sont pas périodiques.
a)
b)

c)
d)
e)
f)

g)
2) Pour les signaux périodiques, indiquer, quand c’est possible, le nombre de
motifs élémentaires que comprend le graphique.
Exercice 2
Pour chacun des signaux périodiques suivants :
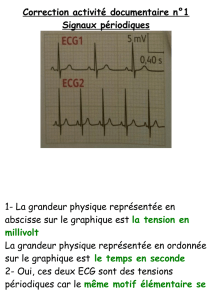
a) Indiquer par lecture graphique la période, la tension maximale et la
tension minimale du signal.
b) Déduire de ces données par le calcul la fréquence du signal.
a)

b)
c)
d)
e)

Exercice 3
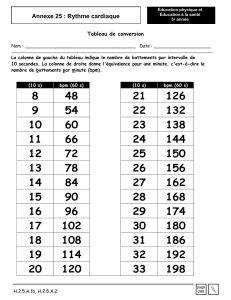
Un coureur cycliste mesure son rythme cardiaque au repos avant de débuter un
entraînement. Son cardio-fréquencemètre mesure 11 battements de cœur pour 15
secondes.
a) Calculer le rythme cardiaque du coureur cycliste au repos en nombre de
battements du cœur par minute.
b) En déduire sa fréquence cardiaque en Hertz puis la période des battements
du cœur.
Au cours de son entraînement, le cycliste aborde à grande vitesse (pour un
cycliste !!) une section plane. Son cardio-fréquencemètre lui indique alors que la
fréquence de son rythme cardiaque est de 0.66 Hz.
c) Déduire de cette indication la période des battements du coeur et le
nombre de battements de cœur par minute.
L’entraînement se termine par une montée assez raide que le cycliste aborde le
plus rapidement possible. La période des battements du cœur du cycliste est
alors de 0,43 s
d) Déterminer la fréquence cardiaque du cycliste. En déduire le nombre de
battements du cœur par minute.
e) Calculer le rapport entre les nombres de battements du cœur par minute à
la fin et au début de l’entraînement.