et f(b) - Maths au lycée Mezeray

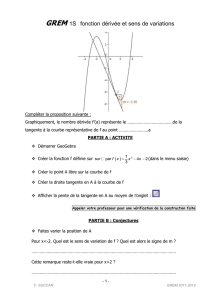
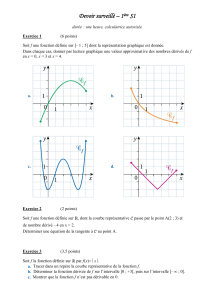
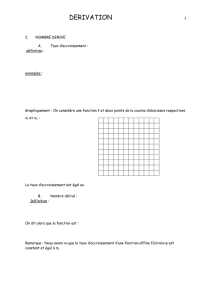
Continuité et théorème des valeurs intermédiaires
I.
1.
2.
Rappels sur la dérivation
Définitions du nombre dérivé

si lim
𝑓(𝑥)− 𝑓(𝑎)
𝑥− 𝑎

si lim
𝑓( 𝑎+ℎ)− 𝑓(𝑎)
ℎ
𝑥→𝑎
ℎ→0
= f '(a) (réel) alors f '(a) est le nombre dérivé en a de f
= f '(a) (réel) alors f '(a) est le nombre dérivé en a de f
Utilisations
a.


Tangente à Cf au point d'abscisse a
Si f est dérivable en a , alors f '(a) est le coefficient directeur de la tangente à 𝑪𝒇 au
point d'abscisse a
Une équation de cette tangente est alors y = f(a) + (x – a) f '(a)
Remarque : Points à tangente horizontale
Si f’(a) = 0 alors 𝐶𝑓 admet au point (a ; f(a)) une tangente parallèle à l’axe des abscisses ( tangente
« horizontale » )
b. Variations d'une fonction

c.

Le signe de la dérivée f’ d’une fonction f sur un intervalle donne les variations de cette
fonction f
 Si, pour tout x de l’intervalle I , f '(x) est positive ( ne s'annulant que pour un nombre
fini de valeurs) alors f est strictement croissante sur I .
 Si, pour tout x de l’intervalle I , f '(x) est négative ( ne s'annulant que pour un nombre
fini de valeurs) alors f est strictement décroissante sur I .
Extrema
si la dérivé de f s’annule en changeant de signe en a alors : f(a) est un extremum local
 f(a) est un maximum local ( intervalle à préciser systématiquement ) si la dérivée est
d’abord négative puis positive .
 f(a) est un minimum local ( intervalle à préciser systématiquement ) si la dérivée est
d’abord positive puis négative .
d. Exemple :
x
f ’(x)
−∞
–2
+ 0
–
3
0
f(–2)
f
–∞
f(3)
5
+ 0
f est strictement croissante sur ]– ∞; −2]
f est strictement décroissante sur [–2 ;3]
f est strictement croissante sur [5 ; + ∞ [
+∞
f(–2) est le maximum de f sur ]– ∞; 3]
f(3) est le minimum de f sur [–2 ; + ∞ [
Le point (5 ;f(5)) est un point à tangente horizontale .
+∞
+
1
3.
Dérivées des fonctions usuelles.
La fonction …
est dérivable sur …
et sa fonction dérivée est …
x  k ( k  I; R )
x x
n
x x
(n  I; N*)
x  Error!
x  Error! (n  Error!)
I; R
I; R
I; R
]- ; 0[ et ]0 ; +[
]- ; 0[ et ]0 ; +[
x 0
x 1
x  nxn–1
x  – Error!
x  – n  Error!
]0 ; +[
x  Error!
x
4.
x
Dérivation et opérations

Dérivée de ku (k  I; R )
Si la fonction u est dérivable sur l'ouvert I alors la fonction ku est dérivable sur I
et sa dérivée est (ku)' = ku'

Dérivée de u + v
Si u et v sont dérivables sur I alors u + v est dérivable sur I et (u + v )' = u' + v'

Dérivée de u  v
Si u et v sont dérivables sur I alors u + v est dérivable sur I et (u  v)' = u'v + uv'

Dérivée de 𝑢²
Si u est dérivables sur I alors u² est dérivable sur I et (u²)' = 2u'u

Dérivée de Error!
𝟏 ′
si u et dérivable sur I et ne s'annulant pas sur I alors Error! est dérivable sur I et (𝒖) = – Error!

Dérivée de
u
v
Si u et v sont dérivables sur I et si v ne s'annule pas sur I alors
u
v
est dérivable sur I et
𝒖 ′
(𝒗) = Error!
II.
Continuité
La notion de continuité nous est familière : le temps s’écoule d’une manière continue, on ne passe pas
brutalement de 12h à 12h 01s, il n’y a pas de saut.
C’est en ce sens que l’expression fonction continue est employée en mathématiques.
2
1. Idée de la notion de continuité:

Intuitivement une fonction continue est une fonction dont la courbe représentative, ne présente
aucun saut, aucun trou, aucune asymptote verticale.
Exemples
2𝑥 − 𝑥²
g(x) = 𝑥² −2𝑥 +
1
La fonction g n’est pas définie pour x = 1
La droite d’équation x = 1 est asymptote à la courbe représentative de
g .
g n’est pas continue en 1
9
8
𝑥 3 − 3𝑥²
7
h(x) =
6
h n’est pas continue en 3, car h n’est pas définie en 3.
Il n’y a pas d’asymptote verticale mais un « trou » pour l’abscisse 3
5
4
2𝑥 − 6
3
 Justifier que la représentation graphique de h est une parabole
privée du point d’abscisse 3 ;
2
1
-5
0
-1 0
5
La fonction « partie entière »
Tout réel x appartenant à un intervalle unique du type
[ p ; p + 1 [ avec p entier relatif , on appelle partie entière de
x, notée E ( x ), l’entier p immédiatement inférieur ou égal à
x


par exemple : E  3 =  2 et E
 3 = 1
La fonction E est définie sur ]−∞; +∞[ mais n’est pas
continue sur ]−∞; +∞[ . Il y a une infinité de points de
discontinuité
2. Continuité et dérivation
Théorème (admis)
Si f est dérivable en « a » alors f est continue en « a » .
Attention ! la réciproque de ce théorème est fausse .
Si f est dérivable sur l’ouvert I alors f est continue sur I .
 Contre-exemples :

la fonction racine carrée en 0
Elle est continue en 0 mais n’est pas dérivable en 0 .
3
Au point (0 ;0) de sa représentation graphique la tangente
est verticale ( en fait la « demi-tangente ») donc ne
possède pas de coefficient directeur ( f’(0) n’existe pas )
Rappel : si f(x) = √𝑥 alors f est définie sur [0 ; + ∞ [ et
dérivable sur ]0 ; + ∞ [ avec f ’(x) =
III.
1
2√𝑥
Théorème des valeurs intermédiaires
1. Préambule
Ce théorème , ou plutôt son corolaire , n’est que la mise en place rigoureuse d’une technique bien connue déjà
depuis la seconde, et comme la démonstration n’est pas au programme ……Il ne reste plus qu’à soigner la
rédaction !!!
exemple
Si on donne le tableau de variation suivant :
x
–∞
–2
1
3
4
+∞
√3
f
–2
0
–∞
Combien l’équation f(x) = – 1 admet-elle de solution ?( les faire apparaître dans le tableau )

Remarque :
Par convention , à partir de maintenant , une flèche dans un tableau de variation indique que la fonction est
continue et strictement monotone sur l’intervalle qui correspond à cette flèche .
Théorème des valeurs intermédiaires
a.
Si f est continue sur un intervalle I et si a ∈ I et b ∈ I
alors :
pour tout réel k compris entre f(a) et f(b) , il existe au moins un réel c de I tel que f(c) = k
c’est à dire que f prend donc au moins une fois toutes les valeurs entre f(a) et f(b) d’où le nom du théorème !
f ( b)
y=k
k
f ( a)
O
a
b
Dans le cas ci-contre , la fonction n’est pas continue sur un
intervalle [ a ; b].
le théorème ne peut s’appliquer , on voit bien , en effet qu’ il
n’existe pas de valeur c dans [ a ; b] telle que f(c) = k
L’équation f(x) = k n’a pas de solution dans [ a ; b].
4
Dans le cas ci-contre , la fonction est continue sur un intervalle
[ 0 ; 5].
Le théorème s’applique :
Pour tout k entre f(0) = 0 et f(5) l’équation f(x) = k admet
au moins une solution dans [0 ;5]
Pour le K du dessin f(x) = K admet même une infinité de solutions du
fait que la fonction est constante sur un intervalle .
b. Corolaire du théorème des valeurs intermédiaires
Si f est continue et strictement monotone sur un intervalle I et si a ∈ I et b ∈ I
alors :
pour tout réel k compris entre f(a) et f(b) , il existe un unique réel c de I tel que f(c) = k
c’est à dire que f prend donc une fois et une seule toutes les valeurs entre f(a) et f(b) .
c’est ce corolaire qui est le plus souvent utilisé .
f ( b)
y=k
k
f ( a)
O

a

b
Attention à bien spécifier « dans [a ;b] » car on ne sait pas si il n’y pas d’autres solutions
ailleurs !
f ( a)
y=k
k
f ( b)
O
Dans le cas ci-contre , la fonction est continue et strictement
croissante sur l’ intervalle [ a ; b].
Le corolaire du théorème des valeurs intermédiaires
s’applique .
Ici on a a < b et , pour tout k de [f(a) ;f(b)] , l’équation
f(x) = k admet une solution unique dans [a ;b] .

a
b
f ( b)
y=k
k
Dans le cas ci-contre , la fonction est continue et strictement
décroissante sur l’ intervalle [ a ; b].
Le corolaire du théorème des valeurs intermédiaires s’applique
.
Ici on a a < b et , pour tout k de [f(b) ;f(a)] , l’équation
f(x) = k admet une solution unique dans [a ;b] .
Dans le cas ci-contre , la fonction est continue mais n’est pas
strictement monotone sur l’ intervalle [ a ; b].
f ( a)
O
a 1
2
3 b
5
Le corolaire du théorème des valeurs intermédiaires ne s’applique pas .
Pour la valeur k du dessin , l’équation f(x) = k admet plusieurs solutions dans [a ; b ] .
Dans le cas ci-contre , la fonction est continue et monotone sur l’ intervalle [
0 ; 4]. Mais n’est pas strictement monotone sur l’ intervalle [ 0 ; 4].
Le corolaire du théorème des valeurs intermédiaires ne s’applique pas .
Pour la valeur k du dessin , l’équation f(x) = k admet une infinité de solutions dans
[ 0 ; 4]. ( tout un intervalle comme ensemble des solutions) .
Exemple : ( et rédaction )
On se propose de trouver le nombre de solutions de l’équation ci-dessous et leurs valeurs approchées
𝑥 3 – 5x² + 7x –1 = 0
6
IV.
Fonctions convexes et fonctions concaves
1. Définition
Soit f est une fonction dérivable sur un intervalle I et soit (C) sa représentation graphique .
f est une fonction convexe sur I si et seulement si (C) est entièrement située au dessus de chacune de
ses tangentes
f est une fonction concave sur I si et seulement si (C) est entièrement située au dessous de chacune de
ses tangentes
Exemples
y
y
5
5
4
4
3
3
2
2
1
-8
-7
-6
-5
-4
-3
-2
-1
1
0
1
2
3
4
5
6
x
-1
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
x
-1
-2
-2
-3
-3
-4
-4
-5
La fonction représentée ci-dessus est une fonction convexe sur [–7 ; 6 ]
Sur le premier dessin on a tracé entièrement les tangentes en quelques points et sur le second dessin , ces
mêmes tangentes sont schématisées conventionnellement par une double flèche .
-7
-6
-5
-4
-3
-2
-1
y
y
5
5
4
4
3
3
2
2
1
1
0
1
2
3
4
5
6
7
x
-7
-6
-5
-4
-3
-2
-1
0
-1
-1
-2
-2
-3
-3
-4
-4
-5
-5
1
2
3
4
5
6
7
x
La fonction représentée ci-dessus est une fonction concave sur [–7 ; 6 ]
7
Exercice 1
La fonction représentée ci-contre est-elle concave sur [–7 ; 6 ] ?
y
5
4
3
2
Donner un intervalle sur lequel la fonction semble concave .
1
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
x
-1
Donner un intervalle sur lequel la fonction semble convexe .
-2
-3
-4
-5
2. Théorème 1 (admis )
Soit f est une fonction dérivable sur un intervalle I .
f est une fonction convexe sur I si et seulement si sa dérivée f’ est croissante sur I
f est une fonction concave sur I si et seulement si sa dérivée f’ est décroissante sur I
Exercice 2
Montrer que la fonction f définie sur IR par f(x) = – 2x² + 3x + 1 est concave sur IR .
Exercice 3
Etudier la convexité de la fonction définie sur IR par
f(x) = 𝑥 3 – 4x² + 5x – 1
3. Théorème 2
Soit f est une fonction dérivable sur un intervalle I et dont la dérivée f’ est elle-même dérivable sur I
On note f’’ ( lire « f seconde » ) la dérivée de f’ et on dit que f’’ est la dérivée seconde de f
f est une fonction convexe sur I si et seulement si sa dérivée seconde f’’ est positive sur I
f est une fonction concave sur I si et seulement si sa dérivée seconde f’’ est négative sur I
Exercice 4
Etudier la convexité de la fonction définie sur IR par
1
4
9
2
f(x) = 𝑥 4 + 𝑥 3 − 𝑥² + 𝑥 + 2
4. Point d’inflexion
y
5
Soit f est une fonction dérivable sur un
intervalle I
Le point A est un point d’inflexion de la
courbe représentative de f lorsque la
courbe traverse sa tangente (T) en ce point .
4
3
2
1
-7
Le point A de la courbe ci-contre est un point d’inflexion
de cette courbe .
Cette courbe possède un autre point d’inflexion , trouvez
le !
A
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
x
-1
-2
-3
-4
-5
8

Remarque :
Si A (a ; f(a)) est un point d’inflexion de la courbe (C) cela signifie que la fonction f représentée par (C) change
d’inflexion en a .
D’où les théorèmes ci-dessous :
Théorème 1
Si la dérivée f’ dune fonction f change de sens de variation en a
alors le point A (a ; f(a)) est un point d’inflexion de la courbe représentative de f .
Théorème 2
Si la dérivée seconde f’’ dune fonction f s’annule en changeant de signe en a
alors le point A (a ; f(a)) est un point d’inflexion de la courbe représentative de f .
C’est ce second théorème qui est le plus pratique et donc le plus souvent employé .
Exercice 5
Déterminer le(s) point(s) d’inflexion de la courbe représentative de la fonction f définie par
f(x) = 𝑥 3 – x² + x – 1
9