Somme de distances dans un tore de PC

Somme de distances dans un tore de PC
Stéphane Vialle
Février 2007
Cet exercice consiste à implanter un calcul de somme de distances entre villes, sur un cluster
de PC.
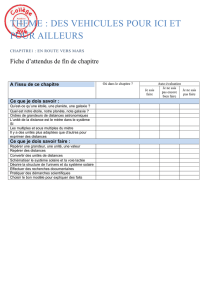
Le cluster de PC : On considère un cluster de PC construit autour d’un simple réseau Fast-
Ethernet. On perçoit ce cluster comme un tore (en dimension deux), et on se limite
volontairement à des communications entre PC voisins. Chaque PC sera identifié par son
numéro de ligne et son numéro de colonne, disponibles dans deux variables : (MaLigne,
MaColonne). On suppose également connu la taille du coté du tore de PC : m.
PC
L : 0
,
C : PC L : 0
,
C : 1 PC L : 0
,
C :
m
-1
PC
L : 1
,
C : PC L : 1
,
C : 1 PC L : 1
,
C :
m
-1
PC
L :
m
-1
,
C : 0 PC L :
m
-1
,
C: 1 PC
L :
m
-1
,
C :
m
-1
La bibliothèque de communication : on considère une bibliothèque proche de MPI. On
suppose disposer d’une instruction Send non bloquante et bufferisée, et d’une instruction
Recv bloquante :
• Send(Ptr sur les données à émettre, taille à émettre, destinataire)
• Recv(Ptr sur la zone à remplir, taille à recevoir, émetteur)
On peut donc émettre les données sans soucis (elles sont sauvegardées automatiquement) et
l’instruction Send rend la main immédiatement. L’instruction Recv bloque jusqu’à ce que les
données soient bien reçues.
Le problème : On considère un ensemble de n villes reliées par un réseau de routes. Toutes
les distances minimales entre les villes sont connues. On dispose d’un tableau (Tab) de nxn
cases, dont la case de coordonnée (ligne l, colonne c) représente la distance minimale pour
aller de la ville l à la ville c.

Distances de la ville V1
vers les autres villes
Distances de toutes les
villes vers la ville Vn-1
V0 V1 Vn-1
V0
V1
Vn-1 Tableau Tab
de nxn cases
Par conséquent, la ligne l contient les distances de la ville l vers toutes les autres. La colonne c
contient les distances de toutes les villes vers la ville c. La distance l → c peut être différente
de la distance c → l (présence de routes à sens unique).
On cherche à identifier la ville « la mieux située » : c’est-à-dire celle dont la somme des n-1
distances vers les autres villes et des n-1 distances depuis les autres villes est la plus petite.
Question 1 : On considère un tore de nxn PC (autant de PC que de cases du tableau, m = n).
Ainsi chaque PC contient une case du tableau :
le PC (ligne l, colonne c) contient la case Tab(ligne l, colonne c)
Concevez et décrivez une circulation de données et un algorithme exécuté sur chaque PC qui
permette à chaque PC de calculer la somme des distances de sa ville vers les autres villes : un
PC de la ligne l calcule la somme des distances de la ville l vers toutes les autres et la stocke
dans sa variable Somme_l. Cet algorithme doit évidemment fonctionner sur tous les PC.
Evidemment, à la fin, tous les PC de la ligne l contiennent la même somme :
0 10 2 12 3 5 8 8
10 0 4 6 16 1 1 1
2 4 1 11 5 2 7 8
…
48 48 48 48 48 48 48 48
39 39 39 39 39 39 39 39
40 40 40 40 40 40 40 40
…
Distribution des distances
entre villes Distribution des sommes
des distances de chaque
ville vers les autres
N’hésitez pas à faire des schémas, donnez bien l’algorithme complet : condition d’arrêt et
valeurs initiales des variables que vous utiliserez.
Question 2 : On considère encore un tore de nxn PC (autant de PC que de cases du tableau).
Concevez et décrivez un algorithme qui permette à chaque PC de coordonnée (l,c) de calculer
la somme des distances de la ville l vers les autres (question précédente) et la somme des

distances des autres villes vers la ville c. Calculez ainsi deux variables (Somme_l, et
Somme_c). Après calculs, vous devez obtenir par exemple :
0 10 2 12
10 0 4 6
2 4 1 11
12 6 11 0
Distribution des distances
entre villes Distribution des sommes
Somme_l et Somme_c
24-24 24-20 24-18 24-29
20-24 20-20 20-18 20-29
18-24 18-20 18-18 18-29
29-24 29-20 29-18 29-29
Ne calculez pas une somme puis l’autre en 2n étapes. Calculez ces deux sommes en n étapes
environ, en concevant une double circulation de données qui utilise les liens horizontaux et
verticaux à chaque étape.
Question 3 : écrivez l’implantation de l’algorithme de la question 2, à l’aide des routines
Send et Recv de l’énoncé. Soyez précis dans l’initialisation des diverses variables employées,
dans les bornes des compteurs de boucles, …
Question 4 : adaptez votre algorithme et votre implantation au cas d’un tore de pxp PC, en
supposant que n = k.p (n est multiple de p).