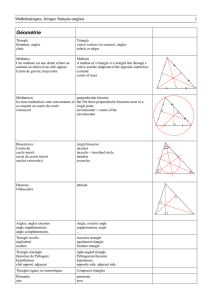
Chapitre 1 TRIANGLES I . Construire un triangle dont on connaît les

Chapitre 1 TRIANGLES
Introduction : On a découvert, dans l'activité 1, que lorsqu'on connaissait uniquement les mesures de deux côtés, de deux
angles, etc, ..., on pouvait construire plusieurs triangles non superposables.
Par contre, il y a des situations où tous les triangles construits sont superposables, ce sont ces trois cas que nous allons
étudier ici :
I . Construire un triangle dont on connaît les longueurs des trois côtés :
1) Peut-on toujours construire un triangle ?
Propriété (admise) : Inégalité triangulaire : (activité 2)
Dans un triangle, la longueur de chaque côté est inférieure à la somme des longueurs des deux autres côtés.
ABACCB
AC ABBC
BCBAAC
Conséquence : En pratique, pour trois longueurs données, si la plus grande est inférieure à la somme des deux
autres, alors on peut construire un triangle avec ces trois longueurs.
Exemples :
a) Avec les longueurs suivantes : 4cm, 9cm et 3cm : Le plus grand côté mesure 9cm, et la somme des deux autres est égale à
7cm, comme 9>7, d'après l'inégalité triangulaire, on ne peut pas construire un tel triangle.
b) Avec les longueurs suivantes : 7cm, 9cm et 5cm : Le plus grand côté mesure 9cm, et la somme des deux autres est égale à
12cm, comme 9<12, d'après l'inégalité triangulaire, on peut construire un tel triangle.
c) Avec les longueurs suivantes : 4cm, 9cm et 5cm : Le plus grand côté mesure 9cm, et la somme des deux autres est égale à
9cm, comme 9=9, d'après l'inégalité triangulaire, un tel triangle est aplati.
Propriété : Si AM+MB=AB, alors le point M appartient au segment [AB].
Propriété : Si le point P appartient au segment [AB]., alors AP+PB=AB
2) Comment le construire ?
On veut construire, s'il existe, un triangle ABC tel que AB = 5 cm, AC = 4 cm et BC = 7 cm.
•Ce triangle existe car le plus grand côté, 7cm est inférieur à la somme des deux autres, 9cm.
•Avant de commencer la construction, il est fort utile de faire une figure à main levée :
•On peut alors construire soigneusement le triangle ABC :
1 2 3
Trace le segment [BC], car c'est le plus
long.
Trace un arc de cercle de centre B et de
rayon 5 cm.
Trace un arc de cercle de centre C et de
rayon 4 cm.
Le point d'intersection de ces deux cercles
est la point A cherché. On trace le triangle
ABC

II . Construire un triangle dont on connaît les longueurs de deux côtés et l'angle compris entre ces deux
côtés :
On veut construire un triangle DEF tel que DE = 3 cm DF = 4 cm et
EDF =30 °
•Avant de commencer la construction, il est fort utile
de faire une figure à main levée :
•On peut alors construire soigneusement le triangle DEF :
1 2 3 4
Trace le segment [DF] car
c'est le plus long.
Trace l'angle
EDF =30 °
Trace un arc de cercle de
centre D et de rayon 3 cm
Le point d'intersection de la
demi-droite avec l'arc de
cercle est le point E cherché.
On trace le triangle DEF.
III. Construire un triangle dont on connaît la longueur d'un côté et les deux angles qui lui sont
adjacents :
On veut construire un triangle IJK tel que IJ = 4 cm,
IJK =60 °
et
JIK =45°
.
•Avant de commencer la construction, il est fort utile
de faire une figure à main levée :
•On peut alors construire soigneusement le triangle IJK :
1 2 3
On trace le segment [IJ], c'est le seul que
l'on connaisse.
On construit les angles
IJK =60 °
et
JIK =45°
.
Le point d'intersection des deux demi-
droites est le point K cherché. On trace
le triangle IJK.