DS Physique n 4 PCSI 2015 - 2016 Conseils :

DS Physique n◦4 PCSI 2015 - 2016
Conseils :
•Le sujet comporte quatre problèmes indépendants (et quelques questions de cours), lisez attenti-
vement l’énoncé du début à la fin et choisissez ensuite par quelle partie commencer (aucun ordre
n’est imposé).
•Ne restez pas “bloqué” trop longtemps sur une question si vous pouvez faire la suite.
•Le correcteur tiendra compte de la présentation et de la rédaction de votre copie : justifiez
rapidement vos affirmations, donnez la valeur littérale simplifiée des résultats en fonction des
données de l’énoncé, vérifiez l’homogénéité et la cohérence (tout résultat non homogène sera
sanctionné). Seuls les résultats encadrés seront corrigés.
•Numérotez vos copies : 1/4, 2/4 .... (si 4 copies).
•L’usage des calculatrices est autorisé.
Unitédecellulesphotovoltaïques
Une utilisation de l’énergie solaire est la production d’énergie électrique par des cellules photovoltaïques.
Ce problème étudie le fonctionnement d’un ensemble de cellules pouvant venir en complément d’autres
dispositifs. L’énergie pourra être stockée dans des batteries d’accumulateurs et restituée à une installation
domestique par l’intermédiaire d’un onduleur.
Les deux parties de ce problème sont totalement indépendantes.
A. Cellules photovoltaïques
Aucune connaissance préalable sur les cellule photovoltaïque, dont le symbole est représenté figure 1
ci-dessous, n’est nécessaire pour résoudre cette partie.
Le comportement d’une cellule photovoltaïque est bien représenté par la fonction caractéristique
i=Isexp u
U0−1−αSE
avec Is= 0,10 nA ; U0= 25,8.10−3V ; S= 12 cm2et α= 0,35 A.W−1où αest le coefficient représentant
les pertes, Sla surface de la cellule et El’éclairement solaire.
i
u
Figure1 – Cellule photovoltaïque
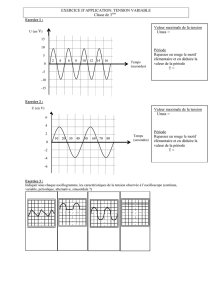
1. Lorsque le flux solaire est maximal, l’éclairement vaut E1= 800 W.m−2; par ciel voilé l’éclairement
vaut E2= 300 W.m−2et par temps gris, E3= 100 W.m−2.
Calculer la tension aux bornes d’une cellule quand elle n’est pas branchée (i= 0) pour les trois
éclairements E1,E2et E3. On notera UC1,UC3et UC3ces trois tensions à vide.Q1
2. Calculer numériquement icc le courant de court-circuit (u= 0) pour les trois éclairements, on les
notera icc1,icc2et icc3.Q2
3. Tracer l’allure des trois caractéristiques sur lesquelles on fera apparaître les points remarquables.
Q3
Lycée Victor Hugo– Besançon Page 1/9 8 Janvier 2016, durée 3 h

DS Physique n◦4 PCSI 2015 - 2016
4. Déterminer l’expression de la puissance fournie Pupar la cellule.Q4
Pour la suite, on envisagera le cas où le flux solaire est maximal E1= 800 W.m−2.
5. On cherche les conditions pour que la puissance Pusoit maximale.
On admettra que dans ces conditions on a : exp u
U0≫1.
Établir la relation permettant de calculer uMax, valeur de ulorsque Puest maximale.
Par une méthode numérique, on trouve uMax = 0,490 V. Calculer la valeur de l’intensité iMax Q5
correspondante.
On branche aux bornes de la cellule une résistance R. Quelle valeur faut-il donner à la résistance
Rpour que ces conditions soient réalisées ?
6. On définit le rendement ηde la cellule comme étant le rapport de la puissance maximale sur la
puissance solaire reçue par toute la surface de la cellule.
Écrire l’expression de η. Faire l’application numérique. Commenter.Q6
Dans le but d’améliorer les performances du dispositif, on cherche à associer les cellules en série
et en parallèle.
7. On met en parallèle npbranches identiques constituées de nscellules en série.Q7
On prendra ns= 50 et np= 25.
Exprimer la tension VDaux bornes du système et l’intensité IDqui le traverse si chaque cellule
fournit sa puissance maximale. Effectuer les applications numériques.
8. Déterminer numériquement la valeur RMde la résistance à brancher aux bornes du capteur solaire
ainsi constitué pour que la condition de puissance maximale soit réalisée.Q8
9. On suppose maintenant que le capteur solaire n’alimente plus une résistance mais charge une
batterie de résistance interne négligeable de 24 V. Quelle est la tension observée aux bornes de
chaque cellule ? Quel courant traverse alors une cellule et la batterie ? Effectuer les applications
numériques.Q9
B. Étude de l’onduleur
Cette partie étudie un onduleur de tension autonome à commande symétrique ou décalée. Un onduleur
est un convertisseur de tension continue en tension alternative. Le montage est celui représenté sur la
figure 2 ci-dessous.
E
K1
K4
LRi
K3
K2
uS
u
Les quatre interrupteurs bidirectionnels K1,K2,K3et K4sont commandés électriquement de telle façon
que :
Pour nT < t < (n+ 1/2)T K1et K3sont fermés K2et K4ouverts
Pour (n+ 1/2)T < t < (n+ 1)T K1et K3sont ouverts K2et K4fermés
Le générateur est une source de tension idéale de force électromotrice Econstante. Lest une inductance
pure dite de lissage et Rreprésente "la charge" c’est à dire ce qui se trouve en aval du circuit. Cette
dernière est modélisée par un résistor de résistance R.
Lycée Victor Hugo– Besançon Page 2/9 8 Janvier 2016, durée 3 h

DS Physique n◦4 PCSI 2015 - 2016
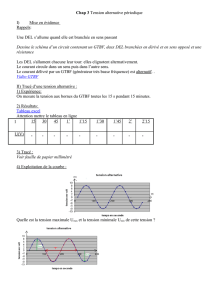
1. Tracer la courbe u(t) en indiquant les points remarquables.Q10
2. Écrire l’équation différentielle vérifiée par i(t), courant circulant dans R.Q11
3. Si i1(t) est la solution de cette équation pour 0 < t < T /2 et i2(t) la solution de cette équation
pour T /2< t < T , déterminer les expressions de i1(t) et i2(t) en fonction de R,Let Eet en
fonction de deux constantes d’intégration A1et A2que l’on ne cherchera pas à calculer pour
l’instant.Q12
On pose τ=L
R.
On se place en régime permanent et on cherche à déterminer les valeurs de A1et A2.
On pose α= exp −T
2τ.
4. Écrire la "condition de raccordement" pour le courant en t=T /2 (c’est à dire la relation liant
i(T−/2) à i(T+/2)) ; justifier.
On obtient ainsi une première équation entre A1et A2.Q13
5. En écrivant que le courant est périodique, écrire une seconde relation entre A1et A2. Résoudre
le système ainsi trouvé.Q14
6. Exprimer i1(t) et i2(t). Tracer le graphe i(t) en faisant apparaître les points remarquables.Q15
Régimetransitoire
On étudie le circuit représenté ci-dessous comportant :
•un interrupteur K,
•un générateur de tension réel modélisé par son équivalent de Thévenin constitué d’une source
idéale de tension de force électromotrice Eet de résistance interne R,
•un condensateur parfait de capacité Cmonté en série avec
•un résistor de résistance Ret enfin
•une bobine considérée comme idéale et d’inductance L
E
RL
i′
R
C
i
K
u
Pour t < 0, le condensateur est déchargé et aucun courant ne circule, on ferme l’interrupteur Kà l’instant
t= 0.
1. Déterminer la valeur de uet ijuste après la fermeture de K, c’est-à-dire à t= 0+.Q16
2. Quelles seront les valeurs de uet ien régime permanent, c’est-à-dire au bout d’un temps très
long en maintenant Kfermé.Q17
3. Établir l’équation différentielle vérifiée par u(t)Q18
4. On règle Let Cde façon à avoir L
R=RC =τ 2où τest une constante. Simplifier l’équation
différentielle précédente en exprimant tous ses coefficients en fonction de τ.Q19
5. Donner l’expression complète de u(t) en fonction de E,τet t.Q20
6. Tracer l’allure de u(t) pour 0 ≤t≤10τen déduire l’allure de i(t) sur la même durée.Q21
Lycée Victor Hugo– Besançon Page 3/9 8 Janvier 2016, durée 3 h

DS Physique n◦4 PCSI 2015 - 2016
Circuitenrégimesinusoïdalforcé
On considère le circuit ci-dessous :
1. En appliquant la loi des nœuds et la loi des mailles, déterminer l’équation différentielle vérifiée
par la tension u(t). Montrer qu’elle se met sous la forme :Q22
¨u(t) + ω0
Q˙u(t) + ω2
0u(t) = ω2 0e(t)
Déterminer les expressions de ω0et Q.
2. On se place en régime sinusoïdal forcé , avec e(t) = Ecos(ωt).Q23
On pose alors u(t) = U0cos(ωt +φ).
En utilisant la méthode de la notation complexe, déduire à partir de l’équation de la question 1,
l’expression de uen fonction de e,ω,ω0et Q.
3. En déduire U0et φen fonction de E,ω,ω0et Q.Q24
4. On propose d’utiliser une autre méthode pour obtenir l’équation différentielle de la question 1).Q25
En utilisant le diviseur de tension, déterminer l’expression de uen fonction de e,R,Let C.
5. En déduire l’expression de uen fonction de e,ω,ω0et Qet vérifier que l’on retrouve l’équationQ26
obtenue à la question 1.
Sondeadaptéepouroscilloscope
1 Impédance d’entrée de l’oscilloscope
L’impédance Z1d’un oscilloscope est assimilable à l’association en parallèle d’une résistance R1= 1,0
MΩ et d’une capacité C1= 20 pF (Figures ci -dessous). On rappelle que 1 pF= 10−12 F.
B
R1C1
A
u
Oscilloscope
B
Z1
A
u
Oscilloscope
Figure1 – Entrée de l’oscilloscope
Lycée Victor Hugo– Besançon Page 4/9 8 Janvier 2016, durée 3 h

DS Physique n◦4 PCSI 2015 - 2016
u(t) est une tension sinusoïdale de pulsation ω.
1. Expliquer pourquoi lors du branchement d’un oscilloscope réel, le circuit est perturbé : c’est-à-Q27
dire que la tension vréelle présente dans le circuit en l’absence de l’oscilloscope est différente de
vmesurée obtenue à l’oscilloscope lorsqu’on le branche.
2. Déterminer l’expression de l’impédance complexe Z1en fonction de R1,C1,ωet du nombreQ28
complexe jtel que j2=−1.
3. Déterminer la valeur numérique Z1du module de cette impédance Z1pour une fréquence f= 1Q29
kHz puis pour f= 100 kHz.
4. Quelle est la valeur théorique de la résistance d’entrée RVd’un voltmètre idéal ? Quel est l’ordreQ30
de grandeur de RVpour un multimètre numérique réel ? Commenter les valeurs précédemment
obtenues pour Z1.
2 Branchement de la sonde [Q]
On branche alors le quadripôle passif [Q] comme indiqué sur les figures ci-dessous.
B′
B
Z1
A′
R2
C2
[Q]
A
vu
Oscilloscope
B′
B
Z1
A′
Z2
[Q]
A
vu
Oscilloscope
Figure2 – Entrée de l’oscilloscope équipé d’une sonde
Il comporte lui aussi un résistor en parallèle avec un condensateur. La résistance du résistor est R2, la
capacité du condensateur est C2. On note Z2son impédance équivalente.
1. On alimente le système avec une source idéale de tension sinusoïdale v(t) = V0cos ωt deQ31
pulsation ωfixée. Exprimer uen fonction de vet des impédances Z1et Z2.
2. En déduire l’expression du rapport u
ven fonction des résistances, capacités et de la pulsation.Q32
3. Montrer que si R1C1=R2C2, on aQ33
u
v=R1 R1+R2
indépendant de la valeur de ω.
4. Calculer les valeurs numériques de R2et C2pour qu’on obtienne u
v=1 10.Q34
5. Montrer que l’impédance d’entrée vue entre les bornes A′et B′est alors Ze= 10Z1. CalculerQ35
son module pour f= 1 kHz puis f= 100 kHz. Commenter.
C. Réglage de [Q]
Ce quadripôle [Q] représente une sonde de mesure que l’on intercale entre le dipôle où on prélève la
tension et l’entrée de l’oscilloscope. R2et C2(ajustable) sont fixées aux valeurs calculées au B. 8.
1. Quel est l’intérêt de cette sonde ?Q36
Lycée Victor Hugo– Besançon Page 5/9 8 Janvier 2016, durée 3 h