QUADRILATERES - Monsieur CHAPON

Collège Ambrussum M. CHAPON
V OCABULAIRE
Le quadrilatère ci-contre est formé des quatre côtés [AD], [DL],
[LS] et [SA].
Les deux autres segments [AL] et [DS] sont ses diagonales.
Les points A, D, L et S sont ses sommets.
Pour nommer un quadrilatère, il suffit de lire les points en suivant
le contour du quadrilatère, dans n’importe quel sens, et en partant
de n’importe quel sommet : il existe donc 8 noms possibles pour
le quadrilatère ci-contre : ADLS, ASLD, DLSA, DASL, LSAD,
LDAS, SADL ou SLDA.
On dit que deux côtés sont opposés s’ils n’ont pas de sommet en commun : ici, [AD] et [LS] sont opposés.
On dit que deux côtés sont consécutifs s’ils ont un sommet en commun : ici, [AD] et [DL] sont consécutifs.
T RAPEZE
Un trapèze est un quadrilatère ayant
deux côtés parallèles. On les appelle les
bases du trapèze.
P ARALLELOGRAMME
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.
Dans un parallélogramme, les diagonales se coupent en leurs
milieux, les côtés opposés sont de même longueur et les angles
opposés sont égaux.
Comment prouver qu’une figure est un parallélogramme ?
- si un quadrilatère a ses diagonales qui se coupent en leurs milieux, alors c’est un parallélogramme.
- si un quadrilatère a les côtés opposés de même longueur, alors c’est un parallélogramme.
- si un quadrilatère possède deux côtés parallèles et de même longueur, alors c’est un parallélogramme.
Comment construire un parallélogramme ?
Avec la règle et l’équerre Avec la règle graduée Avec la règle et le compas
En construisant des côtés parallèles En construisant des diagonales de même
longueur qui se coupent en leur milieux
En construisant des côtés de même
longueur
Quadrilatère
est issu du latin quadri, « quatre » et lateris, « côté
». Toutes les figures
à quatre côtés s’appellent donc des quadrilatères.
Mais avec des parallèles, des perpendiculaires et des longueurs égales, que de
quadrilatères différents on peut faire !…
5
e
Q
Q
U
UA AD DR RI IL LA AT TE ER RE ES S
sommet
côté
A
L
S
D
diagonale
bases

Collège Ambrussum M. CHAPON
LOSANGE
Un losange est un quadrilatère dont les côtés sont de même longueur.
Remarque : les losanges font donc partie de la famille des parallélogrammes …
Dans un losange, les diagonales sont perpendiculaires et se coupent
en leurs milieux, les côtés opposés sont parallèles et les angles
opposés sont égaux.
Comment prouver qu’une figure est un losange ?
- si un quadrilatère a ses diagonales perpendiculaires et qui se coupent en leurs milieux, alors c’est un losange.
- si un parallélogramme a ses diagonales perpendiculaires, alors c’est un losange.
RECTANGLE
Un rectangle est un quadrilatère dont les côtés consécutifs sont perpendiculaires.
Remarque : les rectangles font donc partie de la famille des parallélogrammes …
Dans un rectangle, les diagonales sont de même longueur et se
coupent en leurs milieux, et les côtés opposés sont parallèles et de
même longueur.
Comment prouver qu’une figure est un rectangle ?
- si un quadrilatère a ses diagonales de même longueur et se coupant en leurs milieux, alors c’est un rectangle.
- si un quadrilatère possède au moins trois angles droits, alors c’est un rectangle.
- si un parallélogramme a ses diagonales de même longueur, alors c’est un rectangle.
CARRE
Un carré est un quadrilatère dont les côtés consécutifs sont perpendiculaires et de même longueur.
Remarque : les carrés font donc à la fois partie de la famille des rectangles et de celle des losanges …
Dans un carré, on retrouve à la fois toutes les caractéristiques du
losange et du rectangle.
Comment prouver qu’une figure est un carré ?
Il suffit de prouver que c’est à la fois un rectangle et un losange.
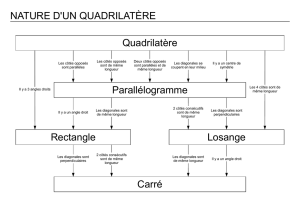
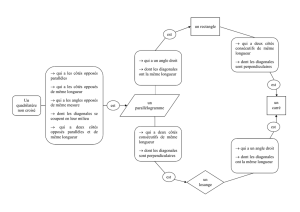
LA FAMILLE DES QUADRILATERES
Voici un schéma qui représente de façon résumée la famille des quadrilatères : en suivant les flèches, tout
quadrilatère a toutes les propriétés des quadrilatères qui le précèdent.
Quadrilatère
Trapèze
Parallélogramme
Rectangle
Carré
Losange
2 côtés parallèles
2 autres côtés parallèles
côtés de même longueur
ou diagonales perpendiculaires
côtés consécutifs perpendiculaires
ou diagonales de même longueur
côtés consécutifs perpendiculaires
ou diagonales de même longueur
côtés de même longueur
ou diagonales perpendiculaires