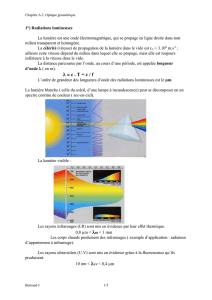
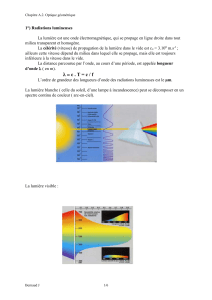
1°) Composants de base permettant de modifier les caractéristiques géométriques... faisceau lumineux : miroirs, fibres optiques, lentilles

Chapitre II Phénomènes vibratoires Cours TS Matériaux Souples
II.2 Optique
Bernaud J 1/6
1°) Composants de base permettant de modifier les caractéristiques géométriques d'un
faisceau lumineux : miroirs, fibres optiques, lentilles
1.1) Définitions
1.1.1) Rayons et faisceaux lumineux
Un rayon lumineux est le trajet suivi par la lumière pour aller d'un point à un
autre.
Le faisceau est un ensemble de rayons issus d'une source lumineuse, il est
« matérialisé » donc visible, quand il rencontre des objets diffusants, qui se comportent
comme des sources de lumière secondaire, en diffusant la lumière dans toutes les directions,
en particulier celle de notre œil..
1.1.2) Miroir
C’est un système optique simple, dont la surface est polie avec ou non dépôt d’une
mince couche de métal.
Symbole:
1.1.3) Fibres optiques
Ce sont des fils de verre très fin comportant un cœur formé d’un verre d’indice n1,
entouré d’une gaine formée d’un verre d’indice n2 < n1. Dans ces conditions, la lumière
se propage à l’intérieur de la fibre optique grâce à une succession de réflexions totales
sur les parois.
L’angle d’incidence restant toujours supérieur à l’angle limite.
1.1.4) Lentilles
C'est un système optique qui utilise le phénomène de réfraction pour la
formation d'image.
1.2) Lois de l’optique
Réflexion :
Angle d’incidence = angle de réflexion ii=ir
Rayon incident
ii
Rayon réfléchi
ir

Chapitre II Phénomènes vibratoires Cours TS Matériaux Souples
II.2 Optique
Bernaud J 2/6
Réfraction : (brusque changement de direction que subit la lumière quand elle traverse
la surface de séparation de deux milieux).
N1 sin i1 = N2 sin i2
N1 : indice absolu de réfraction du milieu 1 par rapport au vide.
N1 = co / c1
C
o : célérité de la lumière dans le vide.
C1 : célérité de la lumière dans le milieu 1.
1.3) Lentilles minces
1.3.1) Généralités
Une lentille sphérique est constituée par un milieu transparent, généralement
en verre, limité par deux surfaces sphériques ou par une surface sphérique et une
surface plane.
Axe principal : ∆
Centres de courbure : O1 et O2.
Rayons de courbure : R1 et R2.
Deux sortes de lentilles peuvent être considérées:
Celles à bords minces Celles à bords épais
Biconvexe Plan convexe Ménisque convexe Biconcave Plan concave Ménisque concave
O1O2
R2 R1
∆
Surface de séparation
Rayon incident I1
Milieu 1
Milieu 2
Rayon réfracté I2

Chapitre II Phénomènes vibratoires Cours TS Matériaux Souples
II.2 Optique
Bernaud J 3/6
Symboles respectifs:
Les lentilles sont dites minces, si leur épaisseur est faible devant les rayons de courbure
des faces.
1.3.2) Marche des rayons lumineux
1.3.2.1) Propriété du centre optique
Tout rayon incident passant par le centre optique O d’une lentille la traverse
sans être dévié.
1.3.2.2) Foyers principaux
Lentilles convergentes Lentilles divergentes
Axe
principal
O
O: centre
optique
Axe
principal
O
O: centre optique
O
Axe
principal
O
O: centre optique
O
Axe
principal
O
O: centre optique
O

Chapitre II Phénomènes vibratoires Cours TS Matériaux Souples
II.2 Optique
Bernaud J 4/6
1.3.2.3) Foyers secondaires. Plans focaux
1.3.3) Distance focale
C’est la distance qui sépare un foyer principal du centre optique.
Distance focale objet : OFo; distance focale image : OFi.
Valeur absolue (OFo ) = valeur absolue (OFi).
C’est une grandeur algébrique, comptée positivement pour une lentille
convergente, négativement pour une lentille divergente.
1.3.4) Vergence d’une lentille
C’est l’inverse de sa distance focale image.
C s’exprime en dioptrie : δ ; OFi en mètre.
1.3.5) Conditions de GAUSS
Ce sont les conditions d’obtention de bonnes images avec des lentilles minces.
- Les rayons lumineux qui traversent la lentille doivent faire un petit angle α avec la
direction de l’axe principale de la lentille.
Axe
principal
O
O: centre optique
O
Axe
principal
O
O: centre optique
O
COF
i
=1

Chapitre II Phénomènes vibratoires Cours TS Matériaux Souples
II.2 Optique
Bernaud J 5/6
- Les points d’incidence des rayons doivent être proches du centre optique de la
lentille; h petit.
1.4) Construction géométrique de l’image d’un objet
Pour déterminer l’image d’un objet AB, il suffit de construire quelques rayons
caractéristiques issus du point B.
1.5) Formules des lentilles minces
1.5.1) Formule de position
Elle permet de trouver la position et la nature de l’image par rapport à l’objet.
Convention : Axe orienté dans le sens de la lumière.
11
ppC+= '
p : représente la distance de l’objet à la lentille;
p’ : représente la distance de l’image à la lentille.
Pour les lentilles convergentes C > 0 et pour les lentilles divergentes C<0.
Si l’objet ou l’image est réel(le), p ou p’ sont comptées positivement; si l’objet
ou l’image est virtuel(le), p ou p’ sont comptées négativement.
h
O
α
Axe
principal
O
O: centre optique