a) Définition Présentation

Spécialité TS INITIATION A L'ALGORITHMIQUE 2010-2011
1
Présentation
a) Définition
Le mot "algorithme" vient du nom de l’auteur persan Al-Khuwarizmi (né vers 780 - mort vers 850) qui a
écrit en langue arabe le plus ancien traité d’algèbre "abrégé de calcul par la complétion et la
simplification" dans lequel il décrivait des procédés de calcul à suivre étape par étape pour résoudre des
problèmes ramenés à des équations.
Dans un premier temps rédiger un algorithme consiste à décrire les différentes étapes de calcul pour
résoudre un problème algébrique, numérique ou décisionnel.
Plus généralement le mot "algorithme" désigne tout procédé de calcul systématique voire automatique.
S’ajoute à cela la notion de "finitude".
On définit parfois les algorithmes de la manière suivante : " un algorithme est une suite finie de règles à
appliquer dans un ordre déterminé à un nombre fini de données pour arriver, en un nombre fini d’étapes,
à un certain résultat et cela indépendamment des données."
Le résultat doit donc s’obtenir en un temps fini.
A propos des "règles à appliquer", il faut entendre un traitement fait sur des données imposé par une
suite "d’instructions" visant à transformer ces données pour arriver au résultat visé.
Ces "instructions" sont de natures diverses selon le type de données au départ.
C’est ce que nous allons préciser.
b) Algorithme et langage de programmation
Un algorithme est rédigé dans un pseudo-langage (en Français).
Il peut ensuite être implémenté dans un langage de programmation donné.
Pourquoi apprendre l’algorithmique pour apprendre à programmer ? En quoi a-t-on besoin d’un langage
spécial, distinct des langages de programmation compréhensibles par les ordinateurs ?
Parce que l’algorithmique exprime les instructions résolvant un problème donné indépendamment des
particularités de tel ou tel langage. Pour prendre une image, si un programme était une dissertation,
l’algorithmique serait le plan, une fois mis de côté la rédaction et l’orthographe. Or, vous savez qu’il vaut
mieux faire d’abord le plan et rédiger ensuite que l’inverse…
Apprendre l’algorithmique, c’est apprendre à manier la structure logique d’un programme informatique.
Il existe de nombreux langages de programmation sur calculatrice ou ordinateur.

Spécialité TS INITIATION A L'ALGORITHMIQUE 2010-2011
2
On peut en citer une liste non exhaustive :
Ti basic (pour calculatrice), Langage C, C++, Visual Basic, COBOL, FORTRAN, Python, Java, JavaScript,
etc. …..
Nous utiliserons dans nos TD le langage TI basic des calculatrices, le langage Visual Basic avec le tableur
Excel, le langage utilisé dans le logiciel de calcul formel Xcas et une approche ludique de la
programmation avec le logiciel Scratch.
II. Quelques exemples d’algorithmes.
Sans le savoir, vous utilisez des algorithmes tous les jours, comme le montre le premier exemple ci-
dessous.
1. Une recette de cuisine.
Voici une recette tirée d’un livre de cuisine :
Se procurer 250 g de chocolat noir, 250 g de beurre,
4 œufs, 250 g de sucre et 75 g de farine.
a. Faire fondre le chocolat au bain-marie ; ajouter le
beurre, mélanger ; ajouter la farine.
b. Battre les œufs en omelette ; ajouter le sucre et
tourner le mélange.
c. Mélanger les deux préparations.
d. Verser dans un moule et faire cuire 45 minutes au
four à 220 °C.
Servir le gâteau froid.
Ce texte décrit les opérations à effectuer
successivement pour faire un moelleux au chocolat.
Il est formé de trois parties distinctes :
- les entrées : ce sont les ingrédients de la
recette, avec les quantités requises.
- le traitement de la recette : il s’agit des phases
a. b. c. et d. qui s’enchaînent séquentiellement ;
- la sortie : c’est le gâteau fini, que l’on doit servir
froid.
2. Une construction géométrique.
On se donne deux points A et B du plan.
a. Tracer le cercle de centre A passant par B.
b. Tracer le cercle de centre B passant par A.
c. Nommer C et D les points d’intersection de ces
cercles.
Construire le polygone ADBC.
Cet algorithme décrit la construction d’un losange
dont une diagonale est [AB].
Les entrées sont les points A et B.
Le traitement de la construction est décrit dans
les phases a. b. et c.
La sortie est le polygone ADBC.
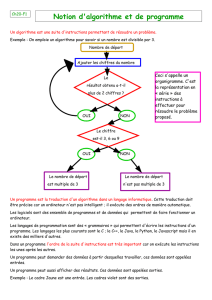
3. Un algorithme de calcul.
Soit deux nombres A et B.
a. Calculer A + B et remplacer A par cette valeur.
b. Calculer A – B et remplacer B par cette valeur.
Afficher A et B.
Cette suite d’instructions est du même type que
les précédentes : les entrées sont les nombres A
et B, le traitement est fait dans les phases a. et
b. et les sorties sont les nombres A et B.
Nous allons faire fonctionner cet algorithme :
- si les entrées sont A = 5 et B = 2, alors à l’étape
a. A + B = 7 et A prend la valeur 7 ;
- à l’étape b. A – B = 7 – 2 = 5, donc B prend la
valeur 5.
Les nombres affichés seront donc : A = 7 et B = 5.
A partir de deux nombres A et B, cet algorithme
affiche leur somme A + B et A.

Spécialité TS INITIATION A L'ALGORITHMIQUE 2010-2011
3
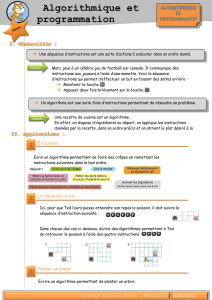
Un
algorithme
est un énoncé d’une suite d’instructions permettant de
donner la réponse à un problème.
Il comprend.
• une phase d’initialisation : on entre les données ;
• une phase de traitement du problème ;
• une phase de sortie des résultats.
II Les éléments de base d’un algorithme simple
a) Les trois étapes
Trois étapes structurent un algorithme simple :
La préparation du traitement
Il s’agit de repérer les données nécessaires à la résolution. Ces données peuvent être numériques, ou
sous forme de textes (on dit souvent chaines de caractères), ou de type logique (deux valeurs possibles,
vrai ou faux), ou enfin de type graphique (des points).
Souvent les données pertinentes doivent être agencées sous une forme plus vaste, comme par exemple
des tableaux ou listes où on peut par exemple ranger commodément les valeurs prises par une fonction
sur un grand nombre de points.
Dans cette phase peut aussi figurer ce qu’on appelle l’entrée des données, qui peut se manifester par la
saisie de caractères ou de nombres sur le clavier, ou la lecture de la position du pointeur de la souris, ou
encore par la lecture d’un fichier contenant ces nombres ou caractères.
Il s’agit aussi de repérer les résultats intermédiaires qu’il est bon de mémoriser pour la suite car
indispensables au traitement.
Il est parfois utile d’utiliser des variables auxiliaires pour ne pas perturber les données initiales.
Le traitement
Il s’agit de déterminer toutes les étapes des traitements à faire et donc des "instructions" à donner
pour une exécution automatique.
Si ces instructions s’exécutent en séquence, on parle d’algorithme séquentiel. Si les opérations
s’exécutent sur plusieurs processeurs en parallèle, on parle d’algorithme parallèle. Si les taches
s’exécutent sur un réseau de processeurs on parle d’algorithme réparti ou distribué. Nous ne traiterons
ici que des algorithmes séquentiels.
La sortie des résultats
Les résultats obtenus peuvent être affichés sur l’écran, ou imprimés sur papier, ou bien encore
conservés dans un fichier. Si on n’en fait rien, ils "restent" en mémoire jusqu’à la prochaine exécution ou
sont perdus. A l’occasion, la sortie pourrait être graphique (afficher ou déplacer le pointeur de la souris
ou des objets sur l’écran) ou sonore … voire sur Internet.

Spécialité TS INITIATION A L'ALGORITHMIQUE 2010-2011
4
b) Les instructions
Les "instructions" sont les "briques de base" des algorithmes, dont l’assemblage dans un ordre précis
conduit au résultat attendu. Nous les présenterons dans un pseudo-langage " en français".
Pour plus de facilité, nous suivrons pas à pas le développement de la formalisation concernant un
algorithme implémentant la suite de Syracuse.
Présentation du problème :
La suite de Syracuse d'un nombre entier N est définie par récurrence, de la manière suivante :
• u
0
= N
• Pour tout entier n naturel :
 si n est pair alors un = n/2;
 si n est impair alors u
n
+1 = 3u
n
+ 1
On se propose d’écrire un algorithme en « pseudo-code » qui en entrée lit l’entier N, calcule et affiche
les 5 premiers termes de cette suite.
Variante : modifier l’algorithme précédent pour s’arrêter au premier terme de la suite égal à 1.
Instructions pour traiter les données
Pour réaliser ces trois étapes évoquées précédemment, on a besoin d’ "instructions de base " comme la
lecture de données, l’affectation de variables et l’écriture de données.
L’affectation de données dans des variables
La formalisation de notre algorithme commence par la connaissance du premier terme de la suite
u
0
. Cette action nécessite de créer une "mémoire" ou variable destinée à cet usage, zone de mémoire a
laquelle il est commode de donner un nom ou identificateur.
Les identificateurs sont des suites de lettres et chiffres (sans espaces) qui doivent être choisies
judicieusement pour que l’algorithme soit immédiatement lisible et interprétable.
Dans notre exemple nous pouvons choisir N pour la variable qui contiendra le résultat du tirage du
premier dé.
Dans notre pseudo-langage en français, nous traduirons l’affectation par l’instruction : identificateur
prend la valeur valeur. ou identificateur valeur
L’affectation remplace la valeur précédente de la variable par la nouvelle. Ainsi l’instruction "A prend la
valeur 2" affecte la valeur 2 à la variable dont A est l’identificateur et ceci quelle que soit la valeur
contenue au préalable dans la variable A.

Spécialité TS INITIATION A L'ALGORITHMIQUE 2010-2011
5
La lecture (ou entrée) des données
La "lecture de données" pourra se faire par interrogation de l’utilisateur ou par extraction a partir d’un fichier
rangé sur un disque voire de données accessibles par Internet.
On a choisi de la traduire par l’instruction : Saisir identificateur.
Par exemple, dans XCAS l’instruction : input(A); va affecter dans la variable nommée A un nombre ou une expression
tapée au clavier.
L’écriture (ou sortie) des données
L’écriture des données permet d’afficher pour l’utilisateur les valeurs des variables après traitement (ou
en cours de traitement dans le cas ou l’on veut contrôler l’exécution). On a choisi de la traduire par
l’instruction : Afficher identificateur. On pourra peaufiner la présentation des résultats pour avoir un
affichage lisible et compréhensible. Une variante consiste à "sortir" directement des informations non
contenues dans une variable, nous le traduirons par : Afficher " message".
Les séquences d’instructions
Le "traitement des données" se fait par une suite d’instructions parmi lesquelles figurent des
affectations d’opérations ou de calculs. Ces opérations ou ces calculs sont spécifiques selon le type des
données utilisées (nombres entiers, nombres décimaux, ou chaines de caractères) ou selon les structures
données utilisées (listes, tableaux, etc.).
Les instructions, simples ou complexes, sont en principe traitées les unes après les autres dans leur
ordre d’apparition dans le programme. Dans la plupart des langages de programmation, les instructions
d’une même séquence sont séparées par un caractère deux-points ou point-virgule ou simplement par un
passage a la ligne.