Leçons de géométrie

Leçons de géométrie
Année scolaire 2009-2010
Classe de CM2a
Caroline SANTELLI

Géom 3
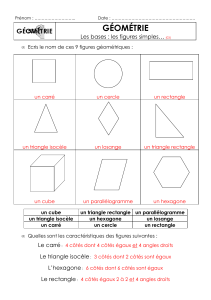
Les polygones
Un polygone est une surface plane délimitée par des segments de droites, les côtés.
Le nom du polygone est défini par le nombre de côtés qu'il possède.
Triangle
Quadrilatère
Pentagone
Hexagone
Octogone
3 côtés
4 côtés
5 côtés
6 côtés
8 côtés
La diagonale est la droite qui relie deux sommets non consécutifs (qui ne se suivent
pas).
Le sommet est le point d'intersection de deux côtés consécutifs.
Géom 4
Les quadrilatères
Un quadrilatère est un polygone qui a 4 côtés.
Il existe des quadrilatères particuliers :
parallélogramme
rectangle
carré
losange
deux côtés opposés
parallèles
Deux côtés opposés
parallèles
Deux côtés opposés
parallèles
Deux côtés opposés
parallèles
des côtés opposés
égaux
Des côtés opposés
égaux
4 côtés égaux
4 côtés égaux
[AB] // [DC] et
[AD] // [BC]
[AB] = [DC] et
[AD] = [BC]
[AB] // [DC] et
[AD] // [BC]
[AB] = [DC] et
[AD] = [BC]
[AB] // [DC] et
[AD] // [BC]
[AB] = [BC] = [CD] =
[DA]
[AB] // [DC] et
[AD] // [BC]
[AB] = [BC] = [CD] =
[DA]
Le rectangle est un
parallélogramme
particulier, il a 4
angles droits.
Le carré est un
losange particulier,
il possède 4 angles
droits.
Les diagonales sont
perpendiculaires, se
coupent en leur
milieu et forment un
angle droit.
Dans un rectangle :
- Les côtés les plus courts sont appelés : largeur (l).
- Les côtés les plus longs sont appelés : longueur (L).
Un carré a 4 côtés égaux, on ne parle pas de longueur et de largeur.

Géom 5
Les triangles
Un triangle est un polygone qui a 3 côtés.
Il existe différents triangles :
1. Le triangle quelconque
Définition :
Il n'a pas de particularité : il a trois côtés, trois angles, et trois sommets.
Construction :
- Avec la règle, trace d'abord un côté (en général la plus grande mesure qu'on te
donne).
- Avec le compas, prend successivement l'écartement correspondant aux mesures des
deux autres côtés.
- Trace le triangle.
2. Le triangle rectangle
Définition :
C'est un triangle qui a un angle droit.
Construction :
- Avec la règle, trace d'abord un côté.
- Avec l'équerre, trace un angle droit au bout du segment. Puis, mesure le segment
pour marquer le deuxième côté.
- Vérifie la mesure du troisième côté et trace le triangle.
3. Le triangle équilatéral
Définition :
Il a trois côtés égaux.
Construction :
- Trace un côté avec la règle.
- Avec le compas reporte les deux autres mesures de côtés.
- Trace les côtés du triangle.
4. Le triangle isocèle
Définition :
Le triangle isocèle a deux angles égaux et deux côtés égaux.
Construction :
- Trace le côté qui n'a pas la même mesure avec la règle.
- Avec le compas, reporte les deux autres mesures sans changer l'écartement.
- Trace les côtés du triangle.
5. Le triangle rectangle isocèle
Définition :
Il possède un angle droit (rectangle) et deux côtés égaux (isocèle).

Géom 7
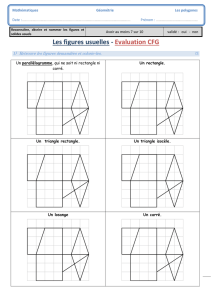
La symétrie axiale
1. Propriétés
La symétrie possède 3 propriétés. On peut dire qu'une forme est symétrique à une
autre forme si :
– la forme symétrique est retournée (en miroir) par rapport à la première forme.
– La distance entre deux points identiques est la même par rapport à l'axe de
symétrie.
– Le symétrique du point choisi est perpendiculaire par rapport à l'axe de
symétrie.
2. A savoir
Une figure possède un axe de symétrie quand on peut la partager en deux parties
et que ces deux parties se superposent exactement.
Le tracé d’une figure symétrique sur un quadrillage : On peut placer les points de la
figure en comptant les carreaux, perpendiculairement à l’axe de symétrie.
Pour tracer une figure symétrique sur une feuille blanche, il est obligatoire de tracer
des perpendiculaires à l’axe de symétrie.
Géom 7
La symétrie axiale
1. Propriétés
La symétrie possède 3 propriétés. On peut dire qu'une forme est symétrique à une
autre forme si :
– la forme symétrique est retournée (en miroir) par rapport à la première forme.
– La distance entre deux points identiques est la même par rapport à l'axe de
symétrie.
– Le symétrique du point choisi est perpendiculaire par rapport à l'axe de
symétrie.
2. A savoir
Une figure possède un axe de symétrie quand on peut la partager en deux parties
et que ces deux parties se superposent exactement.
Le tracé d’une figure symétrique sur un quadrillage : On peut placer les points de la
figure en comptant les carreaux, perpendiculairement à l’axe de symétrie.
Pour tracer une figure symétrique sur une feuille blanche, il est obligatoire de tracer
des perpendiculaires à l’axe de symétrie.