description de l`univers

2nde Univers – Chapitre 1 1/3
DESCRIPTION DE L’UNIVERS
Activité 1 : Du très petit au très grand
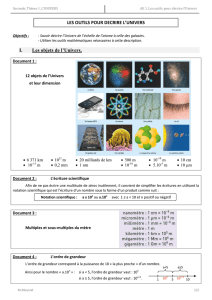
Observer les sept objets de tailles très différentes.
Rappel sur la notation scientifique d’un nombre :
Exprimer un nombre en notation scientifique, c’est l’écrire sous la forme a.10n où n est un entier positif ou négatif,
et a un nombre décimal compris entre 1 et 9.
Questions :
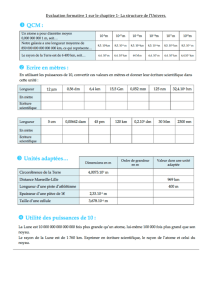
1. Construire le tableau des multiples et sous-multiples du mètre. Convertissez 1 km, 1 mm, 1 m et 1 nm en
mètre, en utilisant l’écriture décimale.
Recopier le tableau ci-dessous sur toute la largeur de votre feuille, puis répondre aux questions 2 (dans les lignes 1
et 2 du tableau), 3 et 4 (dans les lignes 3 et 4 du tableau).
2. Associez à chacune des grandeurs de a à g une longueur parmi celle proposées.
a. Le système solaire
b. La planète Saturne
c. Une coccinelle
d. Un voilier
e. La galaxie spirale M100
f. Des atomes de platine
g. Le virus de la grippe
Cent vingt mille kilomètre ; 12 m ; un milliard de milliards de kilomètre ; 75 nm ; un millième de micromètre ; 5,7
mm ; quinze mille millions de kilomètres.
3. Exprimer les longueurs de la question 2 en mètre écriture décimale.
4. Exprimer les longueurs de la question 2 en mètre écriture scientifique.
Objet ou être
Taille
Taille en mètres (écriture décimale)
Taille en mètres (écriture scientifique)
Ordre de grandeur

2nde Univers – Chapitre 1 2/3
Lire l’encadré suivant, puis répondre aux questions 5 (dans la ligne 5 du tableau) et 6.
5. Donnez, en mètres, l’ordre de grandeur 10n des longueurs de la question 2.
6. L’ordre de grandeur du rayon du noyau atomique est 10-15 m, et l’ordre de grandeur de la taille de l’Univers est
estimé à 1026 m. Graduez un axe de -15 à 26, puis placez-y les valeurs correspondant aux ordres de grandeur
calculés précédemment.
Conclusion : Même unité ; unité légale de longueur dans le système international (SI) ; les préfixes liés aux unités
(tableau) ; l’ordre de grandeur.
Activité 2 : Des grandeurs adaptées aux dimensions de l’Univers
1. Donner la définition de l’unité astronomique (U.A.). Que vaut une unité astronomique en mètre ?
2. Donner la valeur de la vitesse de la lumière dans le vide en mètre par seconde.
3. Combien de temps la lumière met-elle pour parcourir une unité astronomique ?
4. Donner la définition de l’année de lumière (a.l.). Que vaut une année de lumière en mètre ?
5. Sachant que l’étoile polaire se situe à 4,2x106 milliards de kilomètres de la Terre. Calculer cette distance en
année de lumière.
Conclusion : La vitesse de la lumière. L’année de lumière.
Activité 3 : document sur l’Univers…
1. Comment se nomme l’étoile du système solaire ?
2. D’après le document vidéo, quelle est la vitesse de la lumière dans le vide ?
3. Citer les 8 planètes du système solaire et classer les de la plus près à la plus éloignée du Soleil.
4. Quel est le mouvement de chaque planète autour du Soleil ?
5. Qu’est-ce qu’une galaxie ? Comment se nomme la notre ? Citer une autres galaxie.
6. A l’aide du document, compléter le tableau suivant :
Distance
Terre- astre
Lune
Soleil
Neptune
α du
centaure
W Ursa
Majoris
Nébuleuse
d’Orion
Centre de la
Voie Lactée
En km
En « temps
lumière »
7. Les distances de l’étoile W Ursa Majoris et de la nébuleuse d’Orion ne sont pas données en km dans la
vidéo. Pouvez-vous les calculer ?
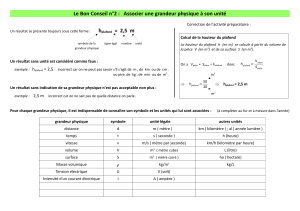
L’ordre de grandeur d’une longueur est une donnée importante. Pour le calculer, il faut procéder de la manière
suivante.
 On exprime la longueur dans une unité adaptée, généralement en mètres, en utilisant la notation scientifique :
a.10n m.
Par exemple : d = 7,25 cm s’écrit d = 7,25.10-2 m.
 On arrondit ensuite a :
- si a est compris entre 1 et 5, on l’arrondit à 1 ;
- si a est égal à 5, ou est compris entre 6 et 9, on l’arrondit à 10.
On obtient alors un nombre qui s’écrit 1.10n ou 1.10n+1 mètres suivant le cas : c’est l’ordre de grandeur de la
longueur considérée. Dans notre exemple, l’ordre de grandeur de d = 7,25 cm est 10-1 m.

8. La lumière met 30 000 ans pour atteindre le centre de notre galaxie, la Voie Lactée. Quelle est la distance
correspondante exprimée en « année-de-lumière » ?
9. Une erreur s’est glissée dans le texte du narrateur : la distance de l’étoile alpha du Centaure par rapport à
la Terre est bien de 4,3 a.l mais la valeur donnée en km est fausse. Pouvez-vous la rectifier ?
Activité 4 : Regarder loin…
Lire le texte suivant et répondre aux questions.
« Nous savons aujourd’hui que, comme le son, la lumière se propage à une vitesse bien déterminée. En
1675, étudiant le mouvement des satellites de Jupiter, l’astronome danois Römer a mis en évidence
certains comportements bizarres. Ces comportements s’expliquent si on admet que la lumière met
quelques dizaines de minutes pour nous arriver de Jupiter. Cela équivaut à une vitesse d’environ trois cent
mille kilomètres par seconde, un million de fois plus vite que le son dans l’air. Il faut bien reconnaître
que, par rapport aux dimensions dont nous parlons maintenant, cette vitesse est plutôt faible. A l’échelle
astronomique, la lumière progresse à pas de tortue. Les nouvelles qu’elle nous apporte ne sont plus
fraîches du tout !
Pour nous, c’est plutôt un avantage. Nous avons trouvé la machine à remonter le temps ! En regardant
« loin », nous regardons « tôt ». La nébuleuse d’Orion nous apparaît telle qu’elle était à la fin de l’Empire
romain, et la galaxie d’Andromède telle qu’elle était au moment de l’apparition des premiers hommes, il
y a deux millions d’année. A l’inverse, d’hypothétiques habitants d’Andromède, munis de puissants
télescopes, pourraient voir aujourd’hui l’éveil de l’humanité sur notre planète… […]
Certains quasars sont situés à douze milliards d’année lumière. La lumière qui nous arrive a voyagé
pendant douze milliards d’années, c’est à dire quatre-vingts pour cent de l’âge de l’Univers… C’est la
jeunesse du monde que leur lumière nous donne à voir au terme de cet incroyable voyage. »
D’après Hubert Reeves, Patience dans l’azur. L’évolution cosmique.
1. A partir des données du texte, donner la vitesse de la lumière en mètre par seconde et calculer la
vitesse du son dans l’air.
2. La galaxie d’Andromède, visible à l’œil nu comme une petite tâche floue par une nuit sans lune,
est distante de 2 200 000 années de lumière. Exprimer cette distance en km.
3. Commenter la dernière phrase du texte en expliquant pourquoi la faible vitesse de la lumière à
l’échelle astronomique est « plutôt un avantage ».
4. Cette lenteur de la lumière à l’échelle astronomique ne présente-t-elle pas un inconvénient
majeur ?
Conclusion : Regarder loin c’est voir dans le passé.
S’autoévaluer !
difficile
Pas évident
Pas de
problème
Savoir que le remplissage de l’espace par la matière est
essentiellement lacunaire aussi bien au niveau de l’atome
qu’à l’échelle cosmique.
Connaître la valeur de la vitesse de la lumière dans le
vide.
Connaître la définition de l’année de lumière et son
intérêt
Expliquer l’expression : « voir loin, c’est voir dans le
passé ».
Savoir utiliser les puissances de 10 dans l’évaluation des
ordres de grandeurs.
.

2nde Univers - Chapitre 1
DESCRIPTION DE L’UNIVERS
Date : / 09 /2010
Salle : salle multimédia
PAILLASSE
MATÉRIEL
ÉLÈVES
BUREAU

2nde Univers – Exercices chapitre 1 1/1
Exercice 1 : Classer des longueurs
1. En utilisant des puissances de 10, exprimer en mètre les longueurs suivantes :
a. diamètre d’un grain de pollen : 33 µm
b. longueur d’une molécule d’eau : 0,4 nm
c. diamètre d’une goutte d’eau : 0,20 mm
d. diamètre du virus de la grippe : 90 nm
e. diamètre de la Terre : 13 * 103 km
f. distance Terre-Soleil : 150 millions de kilomètre
2. Placer ces valeurs et les noms des objets sur un axe gradué en puissance de 10.
Exercice 2 : Communication avec une sonde spatiale
La sonde Voyager II est arrivée à proximité de Neptune en juin 1976. Sachant que Neptune se trouve à environ 4,5.1019 km de
la Terre, combien de temps mettaient les images envoyées par Voyager II par signaux radio pour atteindre la Terre ?
Donnée : les ondes radio se propagent à la même vitesse que la lumière.
Exercice 3 : Voir dans le passé
La constellation de la Baleine est située dans la galaxie Wolf-Lundmark.
a) Calculer la durée que mettrait un signal se propageant à la vitesse c=3.108 m.s-1 émis depuis la Terre pour parvenir dans
cette constellation distante de notre planète de 1,5.1019 km.
b) Exprimer la distance entre la Terre et la constellation de la Baleine en a.l.
c) Si un hypothétique habitant de cette constellation recevait en ce moment même un signal identique en provenance de la
Terre, de quelle période géologique daterait ce signal ?
Donnée : Néogène : de 23 Ma (millions d’années) à 1,65 Ma avant notre ère. Pléistocène : de 1,65 Ma à 10 000 a avant notre
ère. Holocène : période actuelle.
2nde Univers – Exercices chapitre 1 1/1
Exercice 1 : Classer des longueurs
1. En utilisant des puissances de 10, exprimer en mètre les longueurs suivantes :
a. diamètre d’un grain de pollen : 33 µm
b. longueur d’une molécule d’eau : 0,4 nm
c. diamètre d’une goutte d’eau : 0,20 mm
d. diamètre du virus de la grippe : 90 nm
e. diamètre de la Terre : 13 * 103 km
f. distance Terre-Soleil : 150 millions de kilomètre
2. Placer ces valeurs et les noms des objets sur un axe gradué en puissance de 10.
Exercice 2 : Communication avec une sonde spatiale
La sonde Voyager II est arrivée à proximité de Neptune en juin 1976. Sachant que Neptune se trouve à environ 4,5.109 km de
la Terre, combien de temps mettaient les images envoyées par Voyager II par signaux radio pour atteindre la Terre ?
Donnée : les ondes radio se propagent à la même vitesse que la lumière.
Exercice 3 : Voir dans le passé
La constellation de la Baleine est située dans la galaxie Wolf-Lundmark.
1. Calculer la durée que mettrait un signal se propageant à la vitesse c=3.108 m.s-1 émis depuis la Terre pour parvenir dans
cette constellation distante de notre planète de 1,5.1019 km.
2. Exprimer la distance entre la Terre et la constellation de la Baleine en a.l.
3. Si un hypothétique habitant de cette constellation recevait en ce moment même un signal identique en provenance de la
Terre, de quelle période géologique daterait ce signal ?
Donnée : Néogène : de 23 Ma (millions d’années) à 1,65 Ma avant notre ère. Pléistocène : de 1,65 Ma à 10 000 a avant notre
ère. Holocène : période actuelle.