DS alternateur bicyclette Centrale MP 2006 avril

TSI 2 DS Induction Electromagnétique Alternateur de bicyclette 5 avril 2017
Il est essentiel de bien lire le sujet, en repérant bien les différentes grandeurs introduites.
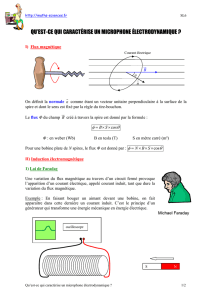
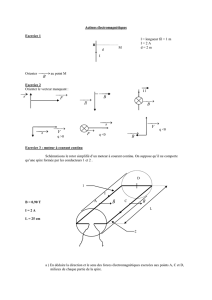
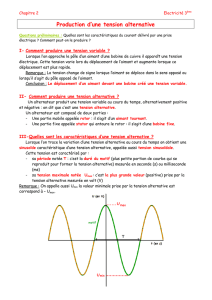
On peut représenter un alternateur de bicyclette de la façon suivante :
• Un aimant permanent (1), caractérisé par un moment magnétique
qui tourne dans le
plan Oyz en faisant avec l’axe (O ,
) un angle = ωt , avec ω constante.
Un aimant de moment magnétique
est équivalent à une boucle de courant (spire)
parcourue par un courant d’intensité i1, de surface S1, telle que
= i1
, S1 étant
supposé beaucoup plus petite que la surface d’une spire de la bobine (2) décrite ci-après.
• Une bobine fixe (2) comportant N tours de fil, chaque tour étant assimilable à une spire de
rayon a, de résistance r et d’inductance L, est placée dans le plan ( O , x , z ) , centrée en O , sa
normale
étant portée par Oy . Cette bobine est branchée en série avec une résistance R
représentant les lampes de la bicyclette, et est parcourue par un courant d’intensité i2 (t).
z
bobine (2)
y
Bobine équivalente à l’aimant permanent (1)
1) On donne l’expression du champ magnétique créé en son centre par la bobine circulaire (2)
de rayon a , d’axe Oy , comportant N spires parcourues par le courant i2( t) :
(O) =
a) Exprimer le flux 21
du champ magnétique créé par la bobine (2) à travers la spire (1)
équivalente à l’aimant permanent.
b) En utilisant les propriétés des coefficients d’inductance mutuelle M12 et M21 de deux
circuits (1) et (2), déduire de ce qui précède le flux magnétique 12 envoyé par l’aimant
permanent (1) dans la bobine (2) de rayon a en fonction du temps t.
On exprimera le résultat en fonction de N , M , a , , t et de la perméabilité magnétique du
vide µ0.
2) En déduire le flux total traversant la bobine (2), puis la force électromotrice d’induction e dont
la bobine est le siège, en fonction de M , N , L , a , i2, et µ0.
3) En déduire l’équation différentielle vérifiée par i2( t) .
4) En régime permanent sinusoïdal, on pose i2 (t ) = I0 s i n ( t + ), I0 étant un nombre réel
positif. Déterminer les expressions de I0 et en fonction des données du problème. On utilisera la
notation complexe. Quelle est la fonction réalisée par ce filtre ?

5) Soit UR l’amplitude de la tension aux bornes de la résistance R. On pose UM =
.
Quelle est la valeur de UM ?
6) Calculer la puissance instantanée absorbée par R.
En déduire la puissance électrique moyenne
<
P
él ec t riq u e
>
absorbée par les lampes de la bicyclette
en fonction de UM , R , L , , r.
7) Rappeler l’expression du couple
exercé sur une boucle de courant (ou un aimant permanent) de
moment magnétique
plongée dans un champ magnétique extérieur
uniforme.
En admettant que le champ créé par la bobine est uniforme au niveau de l’aimant tournant,
calculer le couple instantané qu’il faut appliquer sur l’aimant pour que la vitesse angulaire de
ce dernier soit constante, ainsi que la puissance mécanique instantanée fournie
correspondante en fonction de UM , R , L ,
, r.
8) En passant aux valeurs moyennées dans le temps, établir la relation entre <Pmécanique > et
<Pélectrique > . Quel est le rendement de l’alternateur ainsi modélisé ?

Corrigé DS Alternateur de bicyclette 5 avril 2017
Pour que le corrigé soit plus clair j’ai noté : i1, et non I, le courant circulant dans (1)
i2, et non i, le courant circulant dans (2).
= i1
= i1S1
(O) y
EST-IL NORMAL QUE PLUS DE LA MOITIE DES COPIES NE COMPORTE PAS DE SCHEMA ????
1. a) flux 21
du champ magnétique créé par la bobine (2) à travers la spire (1)
on considère le champ
uniforme sur la surface de la spire (1)
21 =
(O). S1
=
S1cos(t) i2
d’où le coefficient d’induction mutuelle M21 =
S1cos(t)
b) flux magnétique 12 envoyé par l’aimant permanent (1) dans la bobine (2)
12 =
= M21 i1 =
cos(t) S1 i1 =
cos(t)
2. Flux total à travers la bobine (2) : flux du champ
+
à travers (2)
12 + 22 =
cos(t) + NLi2 (chacune des N spires a une inductance L)
3. Fem d’induction, loi de Faraday e = -
=
sin(t) - NL
Cette fem est en série avec la résistance Nr de la bobine et la résistance R des lampes
de la bicyclette
ATTENTION : ne pas compter une 2èm e fois l’inductance propre de la bobine
Loi des mailles : e = (Nr+R) i2
d’où l’équation différentielle : NL
+(Nr+R) i2 =
sin(t) M
4. la solution générale de l’équation différentielle est la somme :
- de la solution générale de l’équation homogène, en exponentielle décroissante
- d’une solution particulière de l’équation complète : comme le second membre est
une fonction sinusoïdale en sin(t), on cherche une solution particulière
sous la forme : i2P (t ) = I0 si n ( t + ),
En régime sinusoïdal permanent i2 (t ) ≈ i2P (t )
On se place alors en complexe : sin(t) est associé à exp(jt)
I0 s i n ( t +) est associé à I0 exp(jt+ )

L’équation différentielle devient : (NLj + Nr + R) I0 exp(jt+ ) =
exp(jt)
D’où I0 exp(j) =
(NLj + Nr + R) soit I0 =
Pour = 0 : I0 = 0 ∞ I0
filtre passe-haut , il faut pédaler !
5. Aux bornes des lampes : uR = Ri2 = R I0 s i n ( t +)
L’amplitude UR de cette tension est R I0
UM =
=
6. puissance instantanée absorbée par R : p = uR . i2 = RI0²sin²(t+)
<pélectrique)> = ½ RI0² =
² (NL² + (Nr + R)²)
7.
=
Couple de Laplace :
=
= -
M sin(t)
= -
M I0 sin ( t +) sin(t)
Ce couple est de sens opposé à la vitesse de rotation
Il faut donc appliquer un couple -
à l’aimant pour qu’il tourne à vitesse constante
Puissance mécanique fournie à l’aimant :
pméca = -
.
=
I0 s i n ( t +) sin(t)
=
I0 [ s i n ( t) cos() + co s ( t) sin () ] sin(t)
Puissance mécanique moyenne fournie à l’aimant :
<Pméca> =
I0 cos()
I0 cos() = Re ( I0 exp())= Re
(NLj + Nr + R)]
=
(Nr+R) (NL² + (Nr + R)²)
<Pméca> =
²(Nr+R) (NL² + (Nr + R)²)
8. d'où le rendement =<pélectrique)> / <Pméca> = R/ (Nr+R)
1
/
4
100%