10 Angles et parallélisme

Chapitre 10 : Angles.
Pré requis : avec les branches du compas prof estimer des angles. Vocabulaire angle plat…
Réactiver la somme des 3 angles dans un triangle quelconque et triangle rectangle.
Présentez un exercice dense pour motiver les positions relatives des angles.
1) Adjacents.
a) Définition.
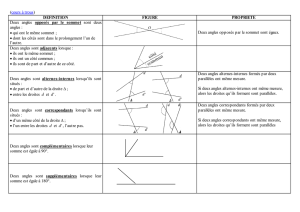
Deux angles adjacents sont deux angles qui ont un sommet commun, un côté commun
et qui sont situés de part et d'autre de ce côté commun.
b) Exemple.
ASB et BSC sont adjacents.
c) Contre-exemples : pas adjacents.
2) Opposés par le sommet.
a) Définition.
Deux angles opposés par le sommet sont deux angles qui ont un sommet commun et qui
ont leurs côtés dans le prolongement l'un de l'autre.
ASM et BSN sont opposés par le sommet.
ASB est opposé par le sommet avec MSN .
ASB n’est pas adjacent à ASC

b) Propriété.
Si 2 angles sont opposés par le sommet alors ils ont la même mesure.
ASM et BSN sont opposés par le sommet. donc ASM = BSN
3) Complémentaires et Supplémentaire.
a) Définition.
2 angles sont complémentaires si leur somme est égale à 90°.
Exemple1 : 40° et 50° sont complémentaires car 40°+ 50° = 90°.
Exemple 2 : Dans un triangle rectangle les 2 angles aigus sont complémentaires.
Contrôler le chapitre sur triangle
b) Définition.
2 angles sont supplémentaires si leur somme est égale à 180°.
Exemple : 70° et 110° sont supplémentaire car 70°+ 110° = 180°.
4) Angles alternes internes
a) Définition.
d et f sont alternes internes.
c et e sont alternes internes.
b) Propriété.
Si dans une figure il y a 2 droites parallèles et une 3ème sécante alors les angles
alternes internes ont la même mesure.
Dans l’exemple d et f sont alternes internes et (d1)//(d2) donc d = f.
c) Propriété.
Si 2 angles alternes internes sont de même mesure alors la figure contient 2 droites
parallèles.
5) Angles alternes externes
a) Définition.

b et h sont alternes externes.
a et g sont alternes externes.
b) Propriété.
Si dans une figure il y a 2 droites parallèles et une 3ème sécante alors les angles
alternes externes ont la même mesure.
Dans l’exemple b et h sont alternes externes et (d1) // (d2) donc b = h.
c) Propriété.
Si 2 angles alternes externes sont de même mesure alors la figure contient 2 droites
parallèles.
6) Angles correspondants.
a) Définition.
a et e sont correspondants.
b et f sont correspondants.
c et g sont correspondants.
d et h sont correspondants.
b) Propriété.
Si dans une figure il y a 2 droites parallèles et une 3ème sécante alors les angles
correspondants ont la même mesure
a et e sont correspondants et (d1)//(d2) donc a = e
c) Propriété.
Si 2 angles correspondants sont de même mesure, alors la figure contient 2 droites
parallèles.
Démonstration somme des angles d’un triangle.