II Comment reconnaitre un quadrilatère ? Quelle est la nature du

II Comment reconnaitre un quadrilatère ?
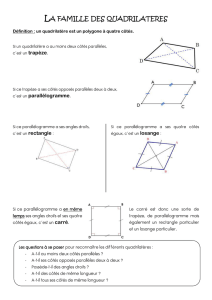
Quelle est la nature du quadrilatère suivant ?
NOIR est un parallélogramme dont l’un des angles est droit.
Idée : Regarder dans les définitions et propriétés les informations
que j’ai.
 Je sais que c’est un parallélogramme dont il a ses côtés
opposés parallèles et de même longueur.
 Je sais qu’il a un angle droit.
 Je peux faire un schéma pour m’aider.
 Ses côtés étant parallèles, il a forcément 4 angles droits.
 Par définition, un parallélogramme qui a 4 angles droits est un
rectangle. Ainsi, NOIR est un rectangle.
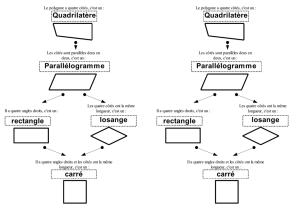
III Comment valider la nature d’un quadrilatère ?
AILE est un quadrilatère dont les côtés sont parallèles 2 à 2 est
un rectangle. Vrai ou Faux.
Soit je peux donner un contre-exemple en expliquant ses propriétés :
Un parallélogramme vérifie les conditions, il a ses côtés parallèles 2 à
2. Ainsi, ce n’est pas nécessairement un rectangle.
Soit j’applique une définition ou propriété de la leçon :
Un quadrilatère qui a ses côtés parallèles 2 à 2 est un
parallélogramme.
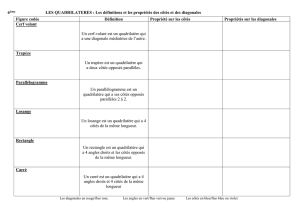
IV Construction d’un quadrilatère
Exemple de construction :
IJKL est un losange dont on connait une diagonale.
Observations :
 La demi-droite d’extrémité I est une diagonale
 Je sais que tous ses côtés sont égaux, ainsi la mesure IJ est
celle des autres côtés aussi.
 A l’aide du compas je vais donc reporter la distance IJ à partir
de J. Le point d’intersection avec la demi-droite est K.
 Je fais de même à partir de K et I, le point d’intersection est L
 Pour finir, il suffit de relier les 4 points.
N
O
I
R