1. Définitions - Collège Mireille Choisy

COLLEGE MIREILLE CHOISY
Classes de CINQUIEME
CONTROLE DE MATHEMATIQUES C2-04
12 février 2010 -
(Les réponses aux questions posées sont en rouge. Les textes en bleu sont des explications.)
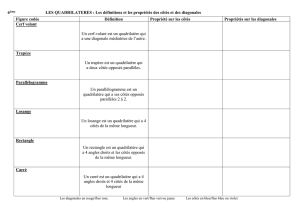
1. Définitions :
a) Parallélogramme.
Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles.
A
B
D
C
Il suffit de tracer deux couples de droites parallèles
b) Rectangle.
Un rectangle est un quadrilatère qui a tous ses angles droits.
MN
QP
Il suffit de tracer trois angles droits avec l’équerre
c) Losange.
Un losange est un quadrilatère qui a ses 4 côtés de même longueur.
F
EG
H
- On trace d’abord l’angle E.
- Puis on place F et H sur les côtés de l’angle E, à
égale distance du point E (avec le compas).
- Enfin, en gardant la même ouverture du compas, on
place G à égale distance de F et de H, de sorte que
FG = HG = EF = EH.
d) Carré.
Un carré est un quadrilatère qui a ses 4 côtés de même longueur et ses 4 angles droits.
R S
UT
On procède comme pour le losange mais on
commence par tracer un angle droit ( R ).
Après avoir placé U et S à égale distance de R,
- soit on trace les angles droits en S et U avec
l’équerre et on obtient le point T,
- soit on place T à égale distance de S et U avec
ST = UT = RS = RU.

2. Parallélogramme IJKL de centre O.
Figure :
IJ
L
K
O
IJKL est un parallélogramme
donc
1) (IJ) // (KL) et (IL) // (JK)
(Les côtés opposés sont parallèles)
2) IJ = KL et IL = JK
(Les côtés opposés ont la même longueur)
3) O milieu de [IK] et O milieu de [JL]
(Les diagonales ont le même milieu)
4) LIJ = JKL et IJK = ILK
(Les angles opposés ont la même mesure)
3. Compléter les phrases :
« Si un quadrilatère a ses côtés opposés parallèles, alors ce quadrilatère est un parallélogramme »
« Si un quadrilatère a ses diagonales qui ont le même milieu, alors ce quadrilatère est un
parallélogramme »
« Si un quadrilatère non croisé a deux côtés opposés parallèles et de même longueur, alors ce
quadrilatère est un parallélogramme »
« Si un quadrilatère non croisé a ses côtés opposés de même longueur, alors ce quadrilatère est un
parallélogramme »
4. Qu’est ce qui distingue un rectangle d’un parallélogramme ordinaire ?
Un rectangle se distingue d’un parallélogramme ordinaire par ses 4 angles droits et par ses
diagonales qui ont la même longueur.
5. Qu’est ce qui distingue un losange d’un parallélogramme ordinaire ?
Un losange se distingue d’un parallélogramme ordinaire par ses 4 côtés de même longueur et par
ses diagonales perpendiculaires.
6. Carré ABCD de centre O.
A
B
DC
O
ABCD est un carré
donc
1) (AB) // (DC) et (AD) // (BC) – Les côtés opposés sont parallèles
2) AB = BC = CD = AD – Les 4 côtés ont la même longueur
3) O milieu de [AC] et de [BD] - Les diagonales ont le même milieu
4) AC = BD – Les diagonales ont la même longueur
5) (AC) ┴ (BD) – Les diagonales sont perpendiculaires
6) A = B = C = D = 90° - Les 4 angles sont droits.

7. Construire un parallélogramme ABCD de centre O tel que : AC = 10 cm, BD = 6 cm
et AOB = 75°.
O
A
C
D
B
5 cm
3 cm
75 °
On trace deux droites sécantes en O et qui forment un angle de 75°.
Sur une des droites on place A et C de sorte que O soit le milieu de [AC] et que AC = 10 cm (OA = OC = 5 cm).
Sur l’autre droite, on place B et D de sorte que O soit le milieu de [BD] et que BD = 6 cm (OB = OD = 3 cm).
8. Construire un parallélogramme PAUL tel que :
PU = 8 cm, LA = 5 cm et LU = 3 cm
L
U
O
A
P
3 cm
4 cm
2,5 cm
On observe d’abord que [PU] et [LA] sont les diagonales et que [LU] est un côté.
On trace un segment [LU] de 3 cm. A l’aide du compas on place un point O à 4 cm de U et à 2,5 cm de L.
On trace la droite (UO) et on place le point P symétrique de U par rapport à O.
On trace la droite (LO) et on place le point A symétrique de L par rapport à O.
O est le milieu de [PU] et de [LA].
PU = UO x 2 = 4 x 2 = 8 cm
LA = LO x 2 = 2,5 x 2 = 5 cm
On trace alors le quadrilatère PAUL qui est bien un parallélogramme car ses diagonales se coupent en leur milieu.