Chapitre n°10 : « Les angles »

6ème3 2009-2010
Chapitre n°10 : «
Chapitre n°10 : « Les angles Les angles » »
I. L'essentiel à connaître parfaitement
Définition
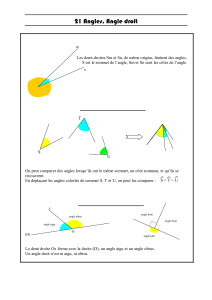
Un angle est constitué de deux demi-droites de même
origine.
Codage
On code un angle à l'aide d'un arc de cercle.
Vocabulaire
•Les deux demi-droites sont appelées les côtés de l'angle.
•L'origine commune est appelée le sommet de l'angle.
Notations d’un angle
On note un angle à l'aide de trois lettres surmontées d'un chapeau. La lettre du milieu
correspond au sommet de l'angle. Les deux autres lettres sont des points situés sur chaque côté
de l'angle.
Par exemple : cet angle se note
RKY
ou
YKR
.
A
O
B
O est le sommet
[OA) et [OB) sont les côtés
Y
R
K

6ème3 2009-2010
Exemple
On considère un triangle
EDT
. On va donner les noms de chaque angle, le sommet, les
côtés et leur nature.
ETD
ou
DTE
a pour
sommet
T
, pour côtés
[TD 
et
[TE 
. Cet angle
« fermé » est un angle aigu.
II. Mesurer un angle
a. 1 ère é tape
Mesurer un angle, c'est mesurer l'ouverture qu'il y a entre les deux côtés de cet angle.
Sans instrument de mesure,
on peut affirmer que la
mesure de l'angle
CAB
est
inférieure à celle de
EDF
.
b. 2 ème étape
L'unité de base pour mesurer un angle est le degré. C'est la plus petite graduation que l'on
observe sur un rapporteur.
On observe sur le rapporteur que les graduations vont de
O
degré à
180
degrés.
Notation : un degré se note
1°
;
47
degrés se note
47°
.
On peut « fabriquer » soi-même
1°
en partageant un demi-cercle en
180
parties égales.

6ème3 2009-2010
c. 3 ème étape
On sait déjà qu'un angle droit mesure
90°
.
Traçons à l'équerre un angle droit puis retrouvons cette mesure de
90°
à l'aide du rapporteur.
On retrouve cette mesure de
90°
en plaçant le centre du rapporteur
sur le sommet. On place le
0
de
l'une des graduations sur l'un des
côtés de l'angle.
On fait attention à bien placer la
partie arrondie du rapporteur entre
les deux côtés de l'angle.
d. 4 ème é tape
Appliquer tout de suite la méthode trouvée pour mesurer ces angles.
(coller feuille polycopiée)
e. Méthode générale
•Le centre du rapporteur sur le sommet.
•Le
0
d'une des deux graduations sur l'un des côtés.
•La partie arrondie située entre les deux côtés.
•Sans se tromper de graduation, on lit la mesure de l'angle.
f. Codage
Lorsqu'on a mesuré un angle,
on peut indiquer cette mesure
directement sur la figure : à
côté du codage.
Polycopié

6ème3 2009-2010
III. Angles particuliers
1/ Angle droit
Définition
Un angle droit est un angle qui mesure
90°
Codage
On code un angle droit à l'aide d'un petit carré dessiné
autour du sommet (à l'intérieur de l'angle).
C'est le codage utilisé pour les droites perpendiculaires !
2/ Angle aigu
Définition
Un angle aigu est un angle dont la mesure est comprise entre
0°
et
90°
.
Illustration
LKM
est un angle aigu ; en effet, il
est contenu dans un angle droit.
3/ Angle obtus
Définition
Un angle obtus est un angle dont la mesure est comprise entre
90°
et
180°
.
Illustration
APX
est un angle obtus car
il peut contenir un angle droit.

6ème3 2009-2010
4/ Angle plat
Définition
Un angle plat est un angle qui
mesure
180°
Remarques
•Si
BAC
est un angle plat alors
A∈[ BC ]
.
•Un angle plat peut contenir deux angles droits. En effet :
180°=90 °90°
.
5/ Nature d'un angle
Lorsqu'on demande la nature d'un angle, il faut dire s'il est aigu, obtus, droit ou plat.
Exemples
•Dans ce triangle, les angles
EGF
,
GEF
,
EFG
sont tous aigus.
•Dans ce triangle, il y a deux angles aigus
ABC
et
BCA
; et un angle obtus
BAC
.
EF
G
A
C
B