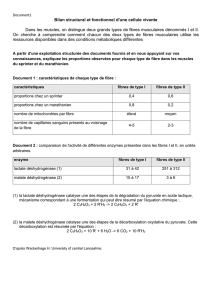
Fibre

http://www.cyber.uhp-nancy.fr/demos/GTRT-004/chap2/c2s4.html
2.4. Fibre optique
2.4.1. Généralités
La lumière est une onde électromagnétique, de longueur d’onde λ, qui se propage dans
un milieu transparent et isolant. (diélectrique)
Avec : λ = C/F où C = Célérité = 3.108 m/s et F = fréquence en Hz
Les équations de Maxwell montrent que la vitesse de propagation dans une substance
diélectrique s'écrit :
V= avec ε = εr.εo et μ = μo.μr :
εo est la permittivité électrique du vide = 1/(36.π.10.9 F/m).
εr est la permittivité relative de la substance par rapport au vide. (sans
dimensions)
μo désigne la perméabilité absolue du vide = 4.π.10-7 H/m.
μr est la perméabilité relative de la substance par rapport au vide. (sans
dimensions)
Ainsi pour εr = 1 et μr = 1 (cas du vide ou de l’air) :
2.4.1. Généralités
2.4.2. Caractéristiques d'une fibre optique
2.4.3. Différents types de fibres optiques
2.4.4. Autres caractéristiques
2.4.5. Raccordement des fibres optiques
2.4.6. Principe du réflectomètre ODTR
2.4.7. Synoptique d'une liaison par fibre optique
2.4.8. Technologie WDM
2.4.9. Câbles à fibres optique

C= = 3.108 m/s
Spectre de la lumière
Dans le domaine des radiations visibles, le spectre s’étend du rouge au violet, ce qui
correspond dans l’air ou dans le vide aux longueurs d’onde suivantes :
Indice optique d’un milieu isolant et transparent
L’indice optique ‘n’ (ou indice de réfraction) d’une substance est donné par :
soit encore :
Remarque : Les milieux isolants (diélectriques) ont une perméabilité
magnétique relative μr ≈ 1.
Pratiquement on obtient : --->
Lois de la réfraction
i = angle d’incidence
r = angle de réfraction

A la traversée de la surface séparant deux milieux transparents d’indices de réfraction
n1 et n2, un rayon lumineux subit une réflexion et une réfraction.
La relation entre angle d’incidence et angle réfracté est donnée par :
n1.sin(i) = n2.sin(r)
Une partie du rayon lumineux est réfléchie dans le milieu d’indice n1, l’autre partie est
réfractée dans le milieu n2.
 L’énergie du rayon réfractée est soustraite de celle du rayon incident, ainsi, au bout de
quelques passages, le rayon fini par être complètement absorbé.
Pour n1 > n2, il existe un angle d’incidence limite IL tel que r = π/2
 Il n’y a plus de rayon réfracté, seul subsiste le rayon réfléchi, le rayon se propage
alors dans la fibre sans atténuation.
Détermination de l’angle limite IL
Pour une réflexion totale il faut : IL ≤ i ≤ π/2 avec : i = - θ
Soit θmax = - IL
n1.sin(i) = n2.sin(r)  sin(i) croit dans le même sens que sin(r)
2.4.2. Caractéristiques d'une fibre optique
Vitesse maxi de l’onde incidente Vimax=C/n1
 Vi=f(θ)=Vimax.cos(θ)
Vitesse maxi de l’onde réfractée Vrmax=C/n2
 Vr=f(r)=Vimax.cos(θ/2–r)
 Pour n2 < n1 Vi croit moins vite que Vr
 r atteint avant i
 n1.sin(IL) = n2.sin( )
IL = arcsin(n2/n1) et θL = - IL

Le revêtement est une couche de plastique qui entoure la fibre optique pour la
renforcer, elle aide à absorber les chocs et permet une protection complémentaire contre
des courbures excessives.
L'armature en fibres permet de protéger le cœur contre les forces d'écrasement et les
tensions mécaniques excessives lors de l'installation.
La gaine extérieure complète la protection mécanique du cœur, elle est
généralement de couleur orange, certains types présentent des couleurs noire ou jaune.
Ouverture numérique d’une fibre optique
L’ouverture numérique caractérise
l’angle maximum θo que peut faire
le faisceau pour assurer sa
propagation dans la fibre
optique.
On écrit : no.sin(θ0) = n1.sin(θ)
On se place dans le cas où i = IL  θ = θL = π/2 – IL  sin(θL) = cos(IL)
Rappel : cos(π/2 – x) = sin(x) et sin(π/2 – x) = cos(x)
Or sin(IL)=n2/n1
 cos(θL)=n2/n1
 sin(θL) =
 sin(θ0L) =
Sin(θ0L) représente l’ouverture numérique d’une fibre optique.

Une grande O.N permet de coupler une grande quantité de lumière
issue d’une source assez divergente (diode DEL).
Vitesse de groupe de l’onde
C’est la rapidité avec laquelle l’énergie lumineuse se propage d’une extrémité à l’autre
du guide d’onde.
Vg = Vφ. cos (θ) avec 0 < θ < θL
Vφ= C/n1
 Vg = C.cos (θ)/n1
 Vg mini = C.cos (θL)/n1 = C .(n2/n1)/n1 = C n2/n1²
 Vg maxi = C/n1
Différence relative des indices de réfraction Δ (donnée fabricant)
, pour n1 n2
Comme ON = , on peut écrire : ON = n1
Remarque : Δ s'exprime en %, soit : Δ% .100, en général: Δ% < 1%
Notion de mode de propagation
Un mode de propagation correspond à un rayon lumineux possédant une inclinaison
donnée.
Un rayon lumineux comprend un nombre fini de faisceaux. (Lois de Fresnel)
Dans une fibre optique, les rayons dont l’inclinaison θ > θL seront perdus car ils
engendrent des réfractés et s’éteignent au bout de quelques rebonds.
On appelle θn, une valeur particulière de θ comprise entre 0 et θL, associée à un mode
de propagation.
Paramètre de dispersion intermodale