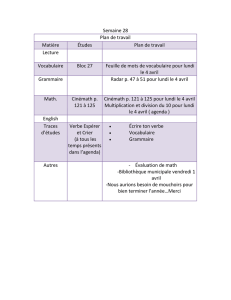
Mémoire - Gaëtan Chenevier

Université Paris XI
Mémoire d’habilitation à diriger des recherches
Spécialité : Mathématiques
Présenté par
Gaëtan CHENEVIER
Représentations galoisiennes automorphes et
conséquences arithmétiques des conjectures de
Langlands et Arthur
Soutenu le 29 Mars 2013
Jury
Laurent CLOZEL Université Paris XI
Michael HARRIS Université Paris VII
Guy HENNIART (Rapporteur) Université Paris XI
Jean LANNES Université Paris VII
Jean-Pierre SERRE Collège de France
Jacques TILOUINE (Rapporteur) Université Paris XIII
Autre rapporteur : Richard TAYLOR, Institute for Advanced Studies, Princeton.

Table des matières
Remerciements iii
Introduction v
Chapitre 1. La fougère infinie des représentations galoisiennes et applications 1
1. Représentations galoisiennes automorphes 1
2. Interlude : variétés de caractères et analogues p-adiques 12
3. La fougère infinie et la densité des points modulaires 20
4. Analogues locaux cristallins 46
Chapitre 2. Quelques conséquences des conjectures de Langlands et Arthur 51
1. Corps de nombres à ramification prescrite : le lemme de Dehn arithmétique. 51
2. Voisins de Kneser des réseaux de Niemeier et formes automorphes pour O(24) 60
3. Motifs de conducteurs 1et quelques problèmes associés 80
4. Quelques cas des conjectures de Bloch-Kato 95
Bibliographie 101
i

Remerciements
Je remercie chaleureusement Michael Harris de m’avoir initié à la théorie des formes
automorphes, et de m’avoir généreusement fait partagé, tout au long de ces dix dernières
années, ses idées stimulantes et sa vision unique sur ce magnifique sujet. Je pense éga-
lement à ma longue et enrichissante collaboration avec Joël Bellaïche, notamment à nos
innombrables discussions sur les conjectures de Langlands et Arthur : merci Joël !
Je voudrais exprimer ma sincère gratitude à Guy Henniart, Richard Taylor et Jacques
Tilouine qui ont accepté d’être rapporteurs de ce travail, et ce malgrè les délais contrai-
gnants qui leurs étaient imposés. Je remercie tout particulièrement Guy Henniart d’avoir
accepté avec enthousiasme d’être le coordinateur de cette habilitation, et aussi pour ses
encouragements. Je suis également très honoré que Laurent Clozel, Michael Harris, Jean
Lannes et Jean-Pierre Serre aient accepté de faire partie de mon jury.
C’est avec grand plaisir que je remercie mes collaborateurs Teodor Banica, Joël Bel-
laïche, Laurent Berger, Julien Bichon, Laurent Clozel, Michael Harris, Chandrashekhar
Khare, Jean Lannes, Michael Larsen, et David Renard, pour les joies que j’ai eues à tra-
vailler avec eux et pour ce qu’ils ont rendu possible. Je suis particulièrement redevable à
Laurent Clozel et Jean Lannes de ce qu’ils m’ont appris. Merci aussi aux autres, qui ont
régulièrement répondu à mes questions, ou avec qui j’ai eu des discussions mathématiques
inspirantes ; je pense notamment à Ahmed Abbes, Nicolas Bergeron, Christophe Breuil,
Emmanuel Breuillard, Kevin Buzzard, Pierre Colmez, Christophe Cornut, Jean-François
Dat, Matthew Emerton, Laurent Fargues, Jean-Pierre Labesse, Vincent Lafforgue, Julien
Marché, Barry Mazur, Colette Moeglin, Fabrice Orgogozo, et Claudio Procesi.
Un survol de ce mémoire suffit pour se rendre compte de toute l’importance dans
ma recherche, parfois même dépendance, des travaux de nombreux mathématiciens. Il
serait maladroit ici de tenter de les énumérer tous, mais leurs apparitions au fil du texte
rendra, je l’espère, claire au lecteur, toute l’admiration que j’ai pour leur travail.
Depuis ma thèse, j’ai eu la chance de bénéficier des ambiances chaleureuses et moti-
vantes de l’équipe de géométrie arithmétique du L.A.G.A., de l’I.H.É.S. et du C.M.L.S.
J’adresse un grand merci à tous mes collègues ou ex-collègues de ces institutions. Merci
aussi à tous ceux ayant rendu techniquement possible cette soutenance !
Merci enfin à tous mes amis que j’ai plaisir à saluer ici. Ma pensée la plus chère va à
Valeria et Julia : merci pour tout le bonheur que vous m’apportez.
iii