LA PARALLAXE D`UNE ETOILE

LA PARALLAXE D'UNE ETOILE
La méthode des parallaxes est excellente, mais elle est très délicate à mettre en œuvre. Il a fallu attendre des moyens d’observation évolués pour
pouvoir l’utiliser, mais alors elle a révolutionné notre connaissance de notre entourage stellaire.
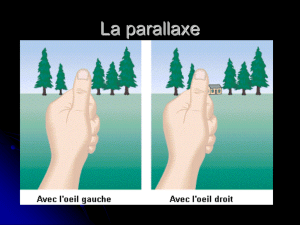
Pour comprendre son principe, faisons une petite expérience. Tendons le bras en avant, index levé. On voit le doigt se profiler devant le mur d’en
face. Si on ferme l’œil droit, on va voir le doigt devant l’image du téléphone. Sans bouger, fermons maintenant l’œil gauche. Le doigt ne se
projette plus devant le téléphone, mais devant le flocon de neige. On va profiter de cela pour mesurer la distance du doigt :
La distance entre les deux yeux produit un effet de perspective, que l’on nomme parallaxe. Cet effet est d’autant plus marqué que l’objet observé
est plus proche, c’est-à-dire que sa distance est plus petite devant l’écart entre les yeux. On peut le mesurer par l’angle que font les rayons
lumineux sur le dessin.
Historiquement, c'est Thalès qui a le premier décrit la méthode ; il l'a utilisée pour mesurer de loin la hauteur d'une pyramide.

Dans le triangle formé par les yeux et le doigt, on connait la distance e entre les yeux, et on mesure l’angle α. On en déduit la distance d. C’est ce
que notre cerveau fait en permanence (vous voyez bien que vous savez calculer un sinus !). Si on ferme un œil, on perd la notion de profondeur.
L’idée des astronomes a été d’augmenter l’écart entre les yeux ! Pour simuler cela, ils ont pris deux photos du ciel à 6 mois d’intervalle. Sur ces
photos, il y a des étoiles très lointaines, qui jouent le rôle du mur, et des étoiles proches qui jouent le rôle du doigt. La distance entre les deux
yeux (les deux photos) est la dimension de l’orbite de la Terre ! 300 millions de kilomètres. Avec cela, on peut espérer mesurer la distance des
étoiles les plus proches.
On connait la base du triangle ; c’est le diamètre de l’orbite terrestre. On mesure l’angle α ; il ne reste plus qu’à résoudre le triangle, pour calculer
l’un des côtés qui n'est autre que la distance qui nous sépare de l'étoile.
On nomme parallaxe l’angle sous lequel on voit le rayon de l’orbite terrestre (et non pas son diamètre
comme sur le schéma ci-dessus ; par l’observation, on mesure l’angle α, et on le divise par deux pour obtenir
la parallaxe de l’étoile). On utilise le rayon de l’orbite terrestre, parce que c’est l’unité astronomique.

Le Parsec
Cette méthode a donné une nouvelle unité de distance : le parsec est la distance correspondant à une parallaxe d’une seconde d'arc ( as).
C’est donc :
1 parsec = distance à laquelle on voit l’Unité Astronomique ( UA) sous un angle d’une seconde d'arc
Abréviation de parsec : pc
Remarque 1 : le parsec est défini à partir de l’unité astronomique, donc les distances entre les étoiles peuvent être mesurées dans la même unité
que les distances dans le système solaire (homogénéité du système d’unités astronomiques). Ce n’est pas le cas avec l’année-lumière, dont la
définition ne fait intervenir que les propriétés de la lumière. On peut toutefois établir des formules de transformation des unités, qui permettront
de passer de l’une à l’autre :
1 pc = 3,26 années-lumière = 206 265 UA (à peu près 3 1013 km)
Cette méthode des parallaxes a permis de mesurer depuis le sol les distances stellaires avec une précision de 10 à 20 % jusqu’à une distance de
30 pc.
Pour sa cohérence avec l’unité astronomique, le parsec présente un grand intérêt, et les astronomes ont tendance à l’utiliser à la place de l’année-
lumière.

Calcul de la distance à l'étoile connaissant la parallaxe de l'étoile
La formule est simple ( et pourrait se démontrer facilement, géométrie élémentaire):
d( en parsec - pc) = 1 : parallaxe (en seconde d'arc - as)
Ce qui en français se traduit par:
La distance entre l'étoile et l'observateur est inversement proportionnelle à la parallaxe de l'étoile .
Autrement dit, plus la parallaxe de l'étoile est petite, plus l'étoile sera loin de nous.
Remarque:
La seconde d'arc (as) est une unité d'angle un peu particulière:
1 as = 1 am /60 où 1am est la minute d'arc
1am = 1°/60
soit 1 as = 1° /3600= 0,00028 ° qui est un angle ultra petit
La seconde d'arc est une unité d'angle bien adaptée à la parallaxe qui est souvent un angle extrêmement petit.
Il n'est pas rare que la parallaxe se mesure en millième de seconde d'arc (mas): 1 mas = 0.001 as = 0,00000028 °

Mesures des parallaxes depuis le sol
Les étoiles sont si loin, que leurs parallaxes sont très faibles, et bien difficiles à mesurer. Impossible à l'œil nu en tous cas, et cette impossibilité à
suscité des oppositions au système héliocentrique de Copernic : puisqu'on ne voit pas de déplacement annuel des étoiles, c'est que la Terre est
fixe !
Il a fallu attendre donc d'avoir de bons instruments pour mettre la parallaxe des étoiles les plus proches en évidence. C'est Bessel qui a publié la
première mesure en 1838, de la parallaxe de l'étoile 61 Cygni (0,29", 11,36 AL, soit 3,48 pc ; 61 Cyg est aussi la première étoile dont on ait
mesuré le mouvement propre). Cette mesure fut une justification supplémentaire de l'héliocentrisme.
La petitesse de la parallaxe de toutes les étoiles (sauf les toutes proches), rend très difficile sa mesure, et les instruments au sol, avec la turbulence
atmosphérique, sont bien limités. Pour progresser, il faut se débarrasser de l'atmosphère, donc observer depuis l'espace. Avant cela, on disposait
seulement des positions de 300 étoiles avec une précision de 10 %.
Même depuis l'espace, seules les étoiles les plus proches seront mesurables. On imagine déjà que pour les plus lointaines, il faudra trouver des
méthodes indirectes. La parallaxe est une mesure équivalente aux mesures que l'on fait sur Terre, par comparaison avec un étalon. De ce fait,
elle sera la base de toute détermination de distance dans l'Univers, d'où son importance.