g =9,81 m/s² pour tous les exercices

T.D. de mécanique des fluides Const
DYNAMIQUE DES FLUIDES 1/5
Date : 1° s.t.i.
Equation de continuité ; théorème de Bernoulli
généralisé ; pertes de charge.
g =9,81 m/s² pour tous les exercices
Equation de continuité
Exercice 1
Lors de l’étude d’un canal d’irrigation on mesure, dans une partie horizontale, ces différentes
grandeurs :
vitesse de l’eau 1,2 m/s
largeur du canal b = 1,5 m
hauteur d’eau h = 0,2 m
Un peu plus loin, dans une partie en pente, la hauteur n’est plus que de h = 0,12m.
1. Quel est le débit en volume et en masse dans le canal ?
2. Quelle est la vitesse de l’eau dans la partie en pente ?
Exercice 2
Dans le cylindre d’un moteur diesel on injecte 0,5 cm3 de gazole durant 1/240e de seconde.
Le piston de la pompe d’injection a un diamètre d1 = 14 mm.
Le passage du gazole, de l’injecteur vers le cylindre, est réalisé par 5 trous de diamètre
d2 = 0,4 mm.
1. Quelle est la durée de l’injection ?
2. Quelle est la surface du pison ?
3. Calculer le débit en volume de cette pompe.
4. Calculer la vitesse supposée uniforme du piston.
5. Quelle est la vitesse du gazole à la sortie des trous d’injecteur ?
Théorème de Bernoulli
Exercice 3
Le niveau de l’eau dans un château d’eau est à l’altitude z1 = 325 m.
Le point le plus bas du réseau de distribution est situé à l’altitude z2 = 240 m.
Le robinet situé en z2 a un diamètre intérieur d = 15 mm.
Remarque : le jet de l’eau en sortie du robinet est entouré d’air à la pression atmosphérique.
1. Faire un dessin de l’installation et préciser la position des points 1 et 2.
2. Calculer la vitesse de l’eau à la sortie du robinet, commenter votre résultat.
3. Quel est le débit en volume et en masse de l’eau à la sortie du robinet ?
Exercice 4
On considère le tuyau d’alimentation d’une lance à incendie à la sortie de la pompe (point 1) et la
lance elle-même (sortie, point 2).On néglige la différence d’altitude entre le point 1 et le point 2.
A la sortie de la pompe la vitesse de l’eau est de v1 = 10 m/s et à la sotie de la lance la vitesse
est de v2 = 100 m/s.
1. Donner la raison pour laquelle la vitesse de l’eau est différente à la sortie de la pompe et à
la sortie du tuyau.
2. Faire un petit schéma de l’installation, en précisant les points 1 et 2 ainsi que les valeurs
connues en chacun de ces points.
3. Calculer la pression de l’eau nécessaire à la sortie de la pompe pour obtenir la vitesse v2.

T.D. de mécanique des fluides Const
DYNAMIQUE DES FLUIDES 2/5
Date : 1° s.t.i.
Equation de continuité ; théorème de Bernoulli
généralisé ; pertes de charge.
2. Calculer la vitesse de l’eau dans la conduite, en appliquant Bernoulli et en utilisant la
relation déterminer au 1.
Exercice 5
Une pompe aspire l’eau d’un puits. La pression (absolue) de l’eau dans la conduite d’aspiration à
l’entrée de la pompe installée à la sortie du puits doit être au moins égale à 40 000 Pa.
La vitesse de l’eau dans la conduite d’aspiration est de v = 3 m/s.
1. Faire un petit schéma du problème en précisant les points 1 et 2 ainsi que les valeurs
connues en chacun de ces points.
2. Déterminer la différence d’altitude entre la surface de l’eau dans le puits et l’entrée de la
pompe.
Exercice 6
Une conduite forcée va d’un barrage réservoir (altitude 850 m) vers une turbine (altitude 650 m)
transformant l’énergie hydraulique en énergie électrique. Le débit maximal est qv = 0,4 m3/s. Et
la vitesse de l’eau dans la conduite doit être inférieure à v = 6 m/s.
1. Faire un petit schéma du problème en précisant les points 1 et 2 ainsi que les valeurs
connues en chacun de ces points.
2. Déterminer le diamètre de la conduite.
3. Déterminer la pression effective maximale à laquelle est soumise la paroi de la conduite.
Exercice 7
L’appareil représenté ci-contre est un capteur de débit utilisant le principe du Venturi.
Un tronçon AB de la conduite, de section S1,
est remplacé par un Venturi essentiellement
constitué par un convergent-divergent. Le
rapport des sections S1 et S2 est connu.
Dans les sections 1 et 2 des trous sont
aménagés pour permettre de placer deux
capteurs de pression reliés à un rack
électronique. Ce rack permet d’afficher soit
p1 - p2 (en bar) soit la vitesse de u1 (en m/s)
du fluide dans la conduite soit directement le
débit qv (en l/s). Les pertes de charge dans
le Venturi sont négligées.
Le fluide qui parcourt la conduite est de
l’eau. Les caractéristiques du Venturi sont les suivantes : S1 = 7854 mm2 et s1/s2 = 1,5. Le rack
affiche p1 - p2 = 0,12 bar.
1. En utilisant l’équation de continuité, déterminer algébriquement U2 en fonction de U1.
3. Déterminer le débit volumique. En déduire U2.
Bernoulli avec transfert d’énergie
Exercice 8
On considère une pompe entre sa bride d’entrée (point 1) et sa bride de sortie (point 2) et on
relève les grandeurs suivantes :
p1 = 100 000 Pa
p2 = 400 000 Pa
c1 = 4 m/s
c2 = 8 m/s
qpompe = 12 dm3/s
z2 - z1 = 1,2 m

T.D. de mécanique des fluides Const
DYNAMIQUE DES FLUIDES 3/5
Date : 1° s.t.i.
Equation de continuité ; théorème de Bernoulli
généralisé ; pertes de charge.
1. Faire un petit schéma du problème en précisant les points 1 et 2 ainsi que les valeurs
connues en chacun de ces points.
2. Déterminer le travail (ou l’énergie) reçu(e) par chaque kilogramme de liquide traversant la
pompe.
3. Déterminer la puissance absorbée par la pompe.
Exercice 9
La figure ci-contre représente l’installation générale
d’une turbine hydraulique pour une hauteur de
chute faible, traversée par un débit de 100m3 par
heure.
1. Déterminer l’énergie cédée par chaque m3
d’eau traversant la turbine
2. Si la turbine à un rendement de 0,9 ;
déterminer la puissance reçue par cette
turbine.
Exercice 10
1
2
Une pompe de refoulement située au fond d’un puits de mine
refoule 80 l.s-1 d'eau de l'altitude - 700 m jusqu'à la surface. L'eau
est pompée dans un bac et arrive dans un autre bac. La vitesse de
l'eau à la sortie est de 6 m.s-1.
1. Déterminer l'énergie apportée par la pompe.
2. Déterminer la puissance de la pompe.
Exercice 11
Les prises de pression en 1 (entrée de la pompe) et en 2 (sortie
de la pompe) sont des prises de pression absolue. Le rack
électronique permet d'intégrer les informations d'un certain
nombre de capteurs et par exemple d'afficher pl-p2.
Le fluide pompé est de l'eau, la tubulure d'aspiration a un
diamètre d1 = 150 mm, la tubulure de refoulement a un
diamètre d2 =100 mm. Le débit volumique, de la pompe est
qv = 15.10-3 m3.s-1. Pour cette valeur, le capteur de pression
différentiel indique : p2 – p1 = 9,8.103 Pa. Le rendement de la
pompe est évalué à η = 0,7.
1. Calculer la vitesse de l'eau en 1 et en 2.
2. Dans la pompe, on néglige les pertes de charge de charge singulières ; calculer le travail
fourni par la pompe (z1 = z2)
3. Calculer la puissance utile et la puissance absorbée
4. On évalue maintenant les pertes de charge singulières dans la pompe à 2,74 J/kg ;
calculer successivement, le travail échangé, la puissance utile et la puissance absorbée.

T.D. de mécanique des fluides Const
DYNAMIQUE DES FLUIDES 4/5
Date : 1° s.t.i.
Equation de continuité ; théorème de Bernoulli
généralisé ; pertes de charge.
Exercice 12
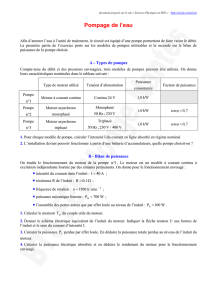
La pompe de circulation d'eau d'un moteur automobile débite 8 m3/h à travers un circuit fermé
moteur radiateur.
La perte de charge totale de ce circuit est évaluée à 6 m de hauteur d'eau.
Nota : Considérer les points 1 et 2 quelconques, mais confondus, du circuit.
5. Faire un petit schéma du problème en précisant les points 1 et 2 ainsi que les valeurs
connues en chacun de ces points.
6. Quelle est la puissance fournie par la pompe pour vaincre cette perte de charge.
Exercice 13
Le jet d'eau d'une fontaine publique est obtenu grâce à une pompe immergée. Le débit d'eau est
de2O l.s-1 et la hauteur du jet est de 10 m.
7. Calculer la vitesse de l’eau au point C (zA= zC et
on rappelle que la vitesse de l'eau en D est
nulle).
8. Calculer le diamètre intérieur du conduit en C.
9. Calculer la pression sachant que le diamètre
intérieur de la conduite en B est de 0,1 m.
10. Calculer la puissance de la pompe si son
rendement est de 0,85.
Exercice 14
L’installation proposée fait partie d’un parc
d’attractions. La pompe aspire de l’eau depuis une
piscine et la refoule en D, haut d’un toboggan, à la
vitesse de 3,5 m.s-1. Les pertes de charge sont
évaluées à 30 J.kg-1 entre A et B, à 25 J.kg-1 entre
C et D.
1. Calculer la puissance de la pompe
nécessaire à l’installation si son rendement
est égal à 0,9.
Bernoulli généralisé
Exercice 15
La pompe de circulation d’eau d’un moteur automobile débite 8 m3/h à travers un circuit fermé
moteur radiateur.
La perte de charge totale de ce circuit est évaluée à 6m de hauteur d’eau.
Nota : Considérer les points 1 et 2 quelconques, mais confondus, du circuit.
1. Faire un petit schéma du problème en précisant les points 1 et 2 ainsi que les valeurs
connues en chacun de ces points.
2. Quelle est la puissance fournie par la pompe pour vaincre cette perte de charge.
Exercice 16
De l’essence à 20 °C (680 kg.m-3) est transporté du port à une cuve de stockage, au moyen
d’une canalisation de 150 mm de diamètre et de 8km de longueur. Le débit est de 180 m3.h-1. La
pompe agit à l’entrée et fournit une pression de 30 bar. La sortie est à la pression atmosphérique
(Patm = 1,013 bar) 180 m plus haut. ε = 0,15 mm ; ν = 1 cst.
1. Faire un petit schéma du problème en précisant les points 1 et 2 ainsi que les valeurs
connues en chacun de ces points.

T.D. de mécanique des fluides Const
DYNAMIQUE DES FLUIDES 5/5
Date : 1° s.t.i.
Equation de continuité ; théorème de Bernoulli
généralisé ; pertes de charge.
2. Déterminer le type d’écoulement.
3. Déterminer le frottement f entre le fluide et la canalisation. En déduire l’énergie perdue
(les pertes de charge linéaire ou régulière) dans la conduite en J/m3 et en J/kg.
4. Déterminer l’énergie apportée et la puissance de la pompe (rendement = 0,85) nécessaire
au transfert de l’essence.
Exercice 17
La canalisation proposée transporte du pétrole.
Elle se compose d’une conduite de diamètre d1 =
30 cm, R1 = 0,005 cm pour la rugosité, longueur
150 m et d’une canalisation d2 = 15 cm, rugosité
R2 = 0,004 cm, longueur 90 m. Le débit est de
0,06 m3.s-1.
ρ = 870 kg.m-3 ; µ = 1,375.10-3 Ns.m-2.
1. Calculer la valeur des pertes de charge singulières.
2. Calculer la valeur des pertes de charge régulières ou linéaires.
3. Calculer la différence de pression P1 - P2 en tenant compte des pertes de charge.
Exercice 18
Une station d’alimentation d’un château d’eau utilise une pompe de puissance nette pn = 12 kW
capable de débiter 24 l/s à une vitesse de 4 m/s. La conduite de refoulement provoque une perte
de charge régulière de 0,12 mètre d’eau par mètre. On donne p = p0 = cte. La conduite est
verticale et on pose l = z2 - z1. La sortie se fait à l’air libre.
1. Calculer le travail échangé W12 entre les sections 1 (canal d’altitude z1) et 2 (château
d’eau d’altitude z2). La pompe est au niveau du canal.
2. Exprimer la perte de charge régulière J12 en fonction de la longueur (z2 - z1) de la conduite
de refoulement (les pertes de charge singulières sont négligées).
3. Quelle différence d’altitude (z2 - z1) peut être atteinte au maximum par cette station ?
Exercice 19
On utilise de nouveau l’exercice de la conduite forcée qui va d’un barrage réservoir (altitude 800
m) vers une turbine (altitude 300 m) transformant l’énergie hydraulique en énergie électrique.
Pour cet exercice, on connaît le diamètre de la conduite d1 = 200 mm de rugosité moyenne
ε = 0,15 mm. La longueur de tuyauterie est l = 1000 m et la tuyère, par laquelle s’échappe l’eau
(dont la température est de 5 °C) et arrive sur la turbine, à un diamètre d2 = 40 mm.
1. Faire un petit schéma du problème en précisant les points 1 et 2 ainsi que les valeurs
connues en chacun de ces points.
Les pertes de charges sont supposées nulles.
2. Calculer la vitesse à la sortie de la tuyère.
3. Calculer la vitesse de l’eau dans la tuyauterie.
Compte tenu des pertes de charge, nous savons que la vitesse de l’eau dans cette conduite est
inférieure au résultat trouvé en 3. Nous allons donc l’évaluer approximativement à 3,5 m/s. Les
pertes de charge singulières seront négligées.
4. Déterminer le type d’écoulement dans la tuyauterie.
5. Déterminer la valeur des pertes de charge.
6. Calculer la vitesse de l’eau à la sortie de la tuyère.
7. Calculer la vitesse de l’eau dans la tuyauterie.
Reprendre le calcul de la conduite avec la vitesse supposée de 3,6 m/s.
8. Calculer les nouvelles valeurs des pertes de charge, de la vitesse à la sortie de la tuyère,
du débit et de la vitesse dans la conduite.